Упражнение 4
Восстановите скобки в следующих формулах:
1. р Ù q É r;
2. Ø q É ( p ÚØ r) Ù q;
3. р É q º р ÙØ r É р Ú q;
4. р Ù q É r º р É (q É r).
При табличном построении логики высказываний логические константы определяются посредством таблиц истинности. При этом принимается, что каждое высказывание имеет одно значение — или “истина”, или “ложь”.
Приведем эти табличные определения логических констант еще раз:
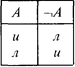
|
| А | В | А Ù В | A Ú В | А É В | А º В |
| и | и | и | и | и | и |
| и | л | л | и | л | л |
| л | и | л | и | и | л |
| л | л | л | л | и | и |
Назовем формулу, являющуюся пропозициональной переменной, элементарной, формулу, содержащую логические константы, — сложной. В сложной формуле можно выделить логическую константу, называемую главной логической константой формулы. Поясним, как это можно сделать.
Каждую сложную формулу логики высказываний можно единственным образом представить в виде Ø А, или А Ù В, или A Ú В, А É В или А º В. Буквами А и В здесь обозначаются формулы, являющиеся частями сложной формулы. Подформулы, конечно, в свою очередь могут быть сложными формулами.
Представив таким образом сложную формулу, мы выделяем в ней последнюю по построению логическую константу, которая и называется главной логической константой формулы.
Найдем главную логическую константу формулы Ø p Ú q É p ÙØ q.
Восстановим скобки в этой формуле:
((Ø p Ú q) É (р ÙØ q)).
Эту формулу единственным образом можно представить в форме А É В. Ее главным знаком является знак импликации. Можно представить в виде “дерева” процесс построения этой формулы:
| р | q | |||
| i | ^ | |||
| ^р | <l | Р | ||
| 1^ | ^ | ^ | ^ | |
| Ьр | V | (pn^q) | ||
| 2 | 4 | |||
| ^ | i |
p q
↓ ↓
Ø p q p Ø q
1↓ ↓ ↓ 3↓
(Ø p Ú q) (p ÙØq)
2 4
↓ ↓
((Ø p Ú q)É(p ÙØq))
5
Стрелки показывают, что из формул (или формулы), от которых они направлены, образована формула, к которой они направлены. Цифры под логическими константами указывают порядковый номер константы по построению формулы. Последняя по построению константа имеет номер 5.
Дата добавления: 2014-12-26; просмотров: 860;
