Центральное поле тяготения
Громоздкой процедуры подбора нужной космической траектории можно избежать, если задаться целью примерно наметить путь космического аппарата. Оказывается, что для сравнительно точных расчетов нет нужды учитывать действующие на КА силы притяжения всех небесных тел или даже сколько-нибудь значительного их числа.
Когда космический аппарат находится в мировом пространстве вдали от планет, достаточно учитывать притяжение одного лишь Солнца, потому что гравитационные ускорения, сообщаемые планетами (вследствие больших расстояний и относительной малости их масс), ничтожно малы по сравнению с ускорением, сообщаемым Солнцем.
Допустим теперь, что мы изучаем движение КА вблизи Земли. Ускорение, сообщаемое этому объекту Солнцем, довольно заметно: оно примерно равно ускорению, сообщаемому Солнцем Земле (около 0,6 см/с2); естественно было бы его учитывать, если нас интересует движение объекта относительно Солнца (учитывается же ускорение Земли в ее годовом движении вокруг Солнца!). Но если нас интересует движение КА относительно Земли, то притяжение Солнца оказывается сравнительно малосущественным. Оно не будет вмешиваться в это движение аналогично тому, как притяжение Земли не вмешивается в относительное движение предметов на борту корабля-спутника. То же касается и притяжения Луны, не говоря уже о притяжениях планет.
Вот почему в космонавтике оказывается весьма удобным при примерных расчетах («в первом приближении») почти всегда рассматривать движение КА под действием одного притягивающего небесного тела, т. е. исследовать движение в рамках ограниченной задачи двух тел. При этом удается получить важные закономерности, которые совершенно ускользнули бы от нашего внимания, если бы мы решились изучать движение космического аппарата под влиянием всех действующих на него сил.
Будем считать небесное тело однородным материальным шаром или по крайней мере шаром, состоящим из вложенных друг в друга однородных сферических слоев (так примерно обстоит дело для Земли и планет). Математически доказывается, что такое небесное тело притягивает так, будто бы вся его масса сосредоточена в его центре (Это неявно предполагалось, когда мы говорили о задаче п тел. Под расстоянием до небесного тела подразумевалось и будет дальше подразумеваться расстояние до его центра). Такое поле тяготения называется центральным или сферическим.
Будем изучать движение в центральном поле тяготения КА, получившего в начальный момент, когда он находился на расстоянии r0 от небесного тела (В дальнейшем для краткости мы будем вместо «небесное тело» говорить «Земля»), скорость v0(r0и v0– начальные условия). Для дальнейшего воспользуемся законом сохранения механической энергии, который справедлив для рассматриваемого случая, так как поле тяготения является потенциальным; наличием же негравитационных сил мы пренебрегаем. Кинетическая энергия космического аппарата равна mv2/2, где т – масса аппарата, a v – его скорость. Потенциальная энергия в центральном поле тяготения выражается формулой
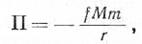
где М – масса притягивающего небесного тела, a r – расстояние от него КА; потенциальная энергия, будучи отрицательной, увеличивается с удалением от Земли, обращаясь в нуль на бесконечности. Тогда закон сохранения полной механической энергии запишется в следующем виде:
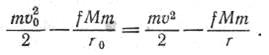
Здесь в левой части равенства стоит сумма кинетической и потенциальной энергий в начальный момент, а в правой – в любой другой момент времени. Сократив на т и преобразовав, мы напишем интеграл энергии – важную формулу, выражающую скорость v космического аппарата на любом расстоянии r от центра притяжения:
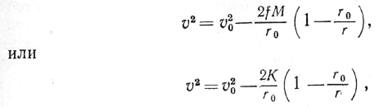
где K=fM – величина, характеризующая поле тяготения конкретного небесного тела (гравитационный параметр). Для Земли К=3,986005·105км3/с2, для Солнца К =1,32712438·1011км3/с2.
Сферические действия планет. Пусть имеются два небесных тела, одно из которых большой массы М, например Солнце, и движущееся вокруг него другое тело значительно меньшей массы m, например Земля или какая-либо другая планета (рис. 2.3).

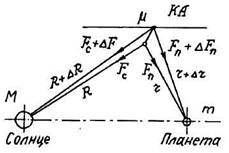 Положим также, что в поле тяготения этих двух тел находится третье тело, например КА, масса которого μ так мала, что практически совершенно не влияет на движение тел массой М и m. В этом случае можно или рассматривать движение тела μ в поле тяготения планеты и по отношению к планете, считая, что притяжение Солнца оказывает возмущающее влияние на движение этого тела, или наоборот, рассматривать движение тела μ в поле тяготения Солнца по отношению к Солнцу, считая, что притяжение планеты оказывает возмущающее влияние на движение этого тела. Для того чтобы выбрать тело, по отношению к которому следует рассматривать движение тела μ в суммарном поле тяготения тел М и m, пользуются введенным Лапласом понятием сферы действия. Область, называемая так, в действительности не является точной сферой, но очень близка к сферической.
Положим также, что в поле тяготения этих двух тел находится третье тело, например КА, масса которого μ так мала, что практически совершенно не влияет на движение тел массой М и m. В этом случае можно или рассматривать движение тела μ в поле тяготения планеты и по отношению к планете, считая, что притяжение Солнца оказывает возмущающее влияние на движение этого тела, или наоборот, рассматривать движение тела μ в поле тяготения Солнца по отношению к Солнцу, считая, что притяжение планеты оказывает возмущающее влияние на движение этого тела. Для того чтобы выбрать тело, по отношению к которому следует рассматривать движение тела μ в суммарном поле тяготения тел М и m, пользуются введенным Лапласом понятием сферы действия. Область, называемая так, в действительности не является точной сферой, но очень близка к сферической.
Сферой действия планеты по отношению к Солнцу называется такая область вокруг планеты, в которой отношение возмущающей силы со стороны Солнца к силе притяжения тела μ планетой меньше, чем отношение возмущающей силы со стороны планеты к силе притяжения тела μ Солнцем.
Пусть М – масса Солнца, m – масса планеты, а μ – масса КА; R и r –расстояния КА соответственно от Солнца и планеты, причем R значительно больше r.
Сила притяжения массы μ Солнцем
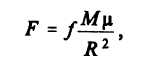
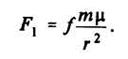
При перемещении тела μ возникнут возмущающие силы
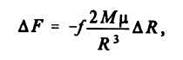
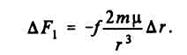
На границе сферы действия, согласно данному выше определению, должно выполняться равенство
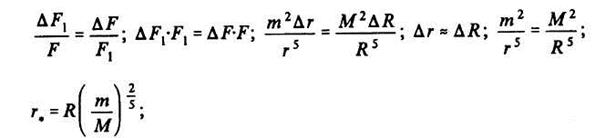
где ro – радиус сферы действия планеты.
Так как r значительно меньше R по условию, то за R обычно принимается расстояние между рассматриваемыми небесными телами. Формула для ro – является приближенной. Зная массы Солнца и планет и расстояния между ними, можно определить радиусы сфер действия планет по отношению к Солнцу (табл. 2.1, где приведен также радиус сферы действия Луны по отношению к Земле).
Таблица 2.1
Сферы действия планет
| Планета | Масса m относительно массы Земли | Расстояние R, в млн км | ro – радиус сферы действия, км |
| Меркурий | 0,053 | 57,91 | 111 780 |
| Венера | 0,815 | 108,21 | 616 960 |
| Земля | 1,000 | 149,6 | 924 820 |
| Марс | 0,107 | 227,9 | 577 630 |
| Юпитер | 318,00 | 778,3 | 48 141 000 |
| Сатурн | 95,22 | 1428,0 | 54 744 000 |
| Уран | 14,55 | 2872,0 | 51 755 000 |
| Нептун | 17,23 | 4498,0 | 86 925 000 |
| Луна | 0,012 | 0,384 | 66 282 |
Таким образом, понятие сферы действия существенно упрощает расчет траекторий движения КА, сводя задачу движения трех тел к нескольким задачам движения двух тел. Такой подход достаточно строг, как показывают сравнительные расчеты, выполненные методами численного интегрирования.
Переходы между орбитами. Движение КА происходит под действием гравитационных сил притяжения. Можно поставить задачи о нахождении оптимальных (с точки зрения минимального требуемого количества топлива или минимального времени на полет) траекторий движения, хотя в общем случае могут быть рассмотрены и другие критерии.
Орбитой называется траектория движения центра масс КА на основном участке полета под действием гравитационных сил. Траектории могут быть эллиптическими, круговыми, гиперболическими или параболическими.
Путем изменения скорости может осуществляться переход КА с одной орбиты на другую, а при выполнении межпланетных полетов КА должен выйти из сферы действия планеты отправления, пройти участок в поле тяготения Солнца и войти в сферу действия планеты назначения (рис. 2.4).
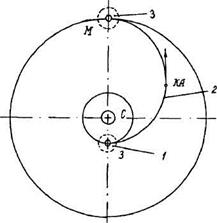
Рис. 2.4. Орбита КА при полете с планеты на планету:
1 – сфера действия планеты отправления; 2 – сфера действия Солнца, эллипс Романа; 3 – сфера действия планеты назначения
КА на первом участке траектории выводится к границе сферы действия планеты отправления с заданными параметрами либо прямо, либо с выходом на промежуточную орбиту спутника (круговая или эллиптическая промежуточная орбита может быть протяженностью менее одного витка или несколько витков). Если скорость КА на границе сферы действия больше или равна местной параболической скорости, тогда дальнейшее движение будет либо по гиперболической или параболической траектории (следует заметить, что выход из сферы действия планеты отправления может быть выполнен по эллиптической орбите, апогей которой лежит на границе сферы действия планеты).
В случае непосредственного выхода на траекторию межпланетного полета (и большой орбитальной скорости) общая продолжительность полета сокращается.
Гелиоцентрическая скорость на границе сферы действия планеты отправления равна векторной сумме выходной скорости относительно планеты отправления и скорости движения самой планеты по орбите вокруг Солнца. В зависимости от выходной гелиоцентрической скорости на границе сферы действия планеты отправления движение будет проходить по эллиптической, параболической или гиперболической траектории.
Орбита КА будет близка к орбите отправления, если гелиоцентрическая скорость выхода КА из сферы действия планеты будет равна ее орбитальной скорости. Если выходная скорость КА больше скорости планеты, но одинакова по направлению, то орбита КА будет располагаться вне орбиты планеты отправления. При меньшей и противоположной по направлению скорости – внутри орбиты планеты отправления. Меняя геоцентрическую скорость выхода, можно получить эллиптические гелиоцентрические орбиты, касательные к орбитам внешних или внутренних планет относительно орбиты планеты отправления. Именно такие орбиты могут служить траекториями полета с Земли к Марсу, Венере, Меркурию и Солнцу.
На конечном этапе межпланетного перелета КА входит в сферу действия планеты прибытия, выходит на орбиту ее спутника и производит посадку в заданном районе.
Относительная скорость, с которой КА войдет в движущуюся ему наперерез или нагоняющую его сзади сферу действия, всегда будет больше местной (на границе сферы действия) параболической скорости в поле тяготения планеты. Поэтому траектории внутри сферы действия планеты назначения всегда будут гиперболами и КА должен неизбежно покинуть ее, если только он не войдет в плотные слои атмосферы планеты или не уменьшит скорость до круговой или эллиптической орбит.

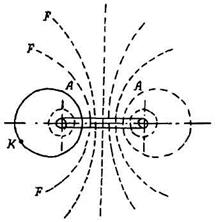 Использование гравитационных сип при полетах в космическом пространстве. Силы гравитации являются функциями координат и обладают свойством консервативности: работа, совершаемая силами поля, не зависит от пути, а зависит только от положения начальной и конечной точек пути. Если начальная и конечная точки совпадают, т.е. путь есть замкнутая кривая, то приращения живой силы не происходит. Однако, встречаются случаи, когда это утверждение неверно: например (рис. 2.5), если в точку К (в электрическом поле вокруг изогнутого проводника, по которому течет ток и в котором силовые линии замкнуты) помещена заряженная частица, то под действием сил поля она будет двигаться по силовой линии и, вернувшись опять в К, будет иметь
Использование гравитационных сип при полетах в космическом пространстве. Силы гравитации являются функциями координат и обладают свойством консервативности: работа, совершаемая силами поля, не зависит от пути, а зависит только от положения начальной и конечной точек пути. Если начальная и конечная точки совпадают, т.е. путь есть замкнутая кривая, то приращения живой силы не происходит. Однако, встречаются случаи, когда это утверждение неверно: например (рис. 2.5), если в точку К (в электрическом поле вокруг изогнутого проводника, по которому течет ток и в котором силовые линии замкнуты) помещена заряженная частица, то под действием сил поля она будет двигаться по силовой линии и, вернувшись опять в К, будет иметь
некоторую живую силу mv2/2 .
Если точка опять опишет замкнутую траекторию, то получит дополнительное приращение живой силы и т.д. Таким образом, можно получить сколь угодно большое увеличение ее кинетической энергии. В этом примере показано, как осуществляется превращение энергии электрического поля в энергию движения точки. Ф. Дж. Дайсон описал возможный принцип устройства «гравитационной машины», использующей для получения работы поля тяжести (Н.Е. Жуковский. Кинематики, статика, динамика точки. Оборонгиз, 1939; Ф. Дж. Дайсон. Межзвездная связь. «Мир», 1965): в Галактике может быть найдена двойная звезда с компонентами А и В, которые вращаются около общего центра масс по некоторой орбите (рис. 2.6). Если масса каждой звезды М, то орбита будет круговой с радиусом R. Скорость каждой звезды нетрудно найти из равенства силы притяжения центробежной силе:
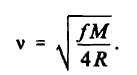
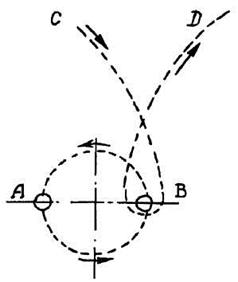
 По направлению к этой системе движется тело С небольшой массы по траектории CD. Траектория рассчитана так, что тело С подходит близко к звезде В в тот момент, когда эта звезда движется навстречу телу С. Тогда тело С совершит оборот вокруг звезды и далее будет двигаться с увеличенной скоростью. От этого маневра получится почти такой же эффект, как от упругого столкновения тела С со звездой В: скорость тела С будет приблизительно равна 2v. Источником энергии при таком маневре является гравитационный потенциал тел А и В. Если тело С – космический аппарат, то он таким образом получает для дальнейшего полета энергию от поля тяжести за счет взаимного притяжения двух звезд. Таким образом, возможен разгон КА до скорости в тысячи километров в секунду.
По направлению к этой системе движется тело С небольшой массы по траектории CD. Траектория рассчитана так, что тело С подходит близко к звезде В в тот момент, когда эта звезда движется навстречу телу С. Тогда тело С совершит оборот вокруг звезды и далее будет двигаться с увеличенной скоростью. От этого маневра получится почти такой же эффект, как от упругого столкновения тела С со звездой В: скорость тела С будет приблизительно равна 2v. Источником энергии при таком маневре является гравитационный потенциал тел А и В. Если тело С – космический аппарат, то он таким образом получает для дальнейшего полета энергию от поля тяжести за счет взаимного притяжения двух звезд. Таким образом, возможен разгон КА до скорости в тысячи километров в секунду.
Дата добавления: 2014-12-26; просмотров: 3603;
