Расчет поля кругового тока
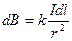
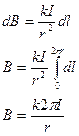
Соленоид — это односложная катушка цилиндрической формы, витки которой намотаны вплотную, а длина значительно больше диаметра. Характеризуется значительным соотношением длины намотки к диаметру оправки, что позволяет создать внутри катушки относительно равномерное магнитное поле.
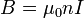 (СИ),
(СИ),
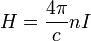 (СГС),
(СГС),
где 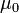 — магнитная проницаемость вакуума,
— магнитная проницаемость вакуума, 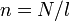 — число витков N на единицу длины l (линейная плотность витков),
— число витков N на единицу длины l (линейная плотность витков), 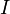 — ток в обмотке.
— ток в обмотке.
53.Циркуляция вектора В вдоль замкнутого контура равна 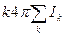 , если контур охватил токи и равна нулю, если контур не охватил токи
, если контур охватил токи и равна нулю, если контур не охватил токи

Закон полного тока для магнитного поля в вакууме циркуляция вектора В по произвольному замкнутому контуру равна произведению магнитной постоянной m0 на алгебраическую сумму токов, охватываемых этим контуром:
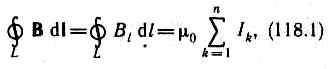
где n — число проводников с токами, охватываемых контуром L произвольной формы. Каждый ток учитывается столько раз, сколько раз он охватывается контуром. Положительным считается ток, направление которого связано с направлением обхода по контуру правилом правого винта; ток противоположного направления считается отрицательным. Например, для системы токов, изображенных на рис. 173,
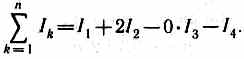
Выражение (118.1) справедливо только для поля в вакууме
Теаорема Гаусса для магнитной индукции показывает, что магнитное поле является (полностью) вихревым..
Линии магнитной индукции непрерывны: они не имеют ни начала, ни конца. Это имеет место для любого магнитного поля, вызванного какими угодно контурами с током. Векторные поля, обладающие непрерывными линиями, получили название вихревых полей.
54.
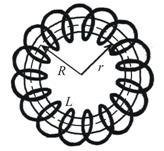

Тороид — это катушка в форме тора.
Выберем замкнутый контур в виде окружности радиуса r с центром, расположенным в центре тора. Выбранный контур проходит внутри тора. Учитывая симметрию задачи, вычислим циркуляцию вектора 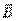 по этому контуру:
по этому контуру:
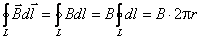 .
.
Теперь воспользуемся теоремой о циркуляции магнитного поля:
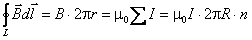 .
.
Здесь R — радиус тороида, 2pR×n — полное число витков тороида, так как n — число витков на единице длины тороида.
Последнее выражение позволяет вычислить индукцию магнитного поля тороида:
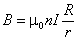 . (9.18)
. (9.18)
Повсюду вне тороида магнитное поле отсутствует, так как для любого контура, проходящего вне тороида, алгебраическая сумма охватываемых токов равна нулю.
55.Сила лоренца – это сила, действующая на заряд q, движущийся с мгновенной скоростью в магнитном поле с индукцией В:
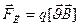
Модуль силы Лоренца:
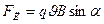 , где
, где 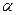 - угол между векторами скорости и индукции, q – модуль заряда частицы
- угол между векторами скорости и индукции, q – модуль заряда частицы
Направление силы Лоренца определяется по правилу правого буравчика: если вращать рукоятку буравчика от вектора скорости к вектору индукции по кратчайшему направлению, то поступательное движение буравчика определит направление силы Лоренца
56. Эффе́кт Хо́лла — явление возникновения поперечной разности потенциалов (называемой также холловским напряжением) при помещении проводника с постоянным током в магнитное поле.
Если через полупроводник в одном направлении пропускать постоянный ток I плотностью j, а в другом направлении воздействовать магнитным полем B, то в третьем направлении можно измерить напряжение U, меняющееся пропорционально силе магнитного поля:
U = R · B · l · j,
где R – постоянная Холла, l– расстояние между гранями, на которых возникает измеряемое напряжение.
Коэффициент 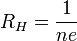 пропорциональности между
пропорциональности между 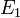 и
и 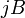 называется коэффициентом (или константой) Холла.
называется коэффициентом (или константой) Холла.
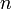 — концентрация носителей заряда.
— концентрация носителей заряда.
57. Работа, совершаемая проводником с током при перемещении, численно равна произведению тока на магнитный поток, пересечённый этим проводником.
Формула остаётся справедливой, если проводник любой формы движется под любым углом к линиям вектора магнитной индукции.
общая работа по перемещению контура
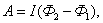 или
или
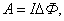
здесь 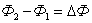 – это изменение магнитного потока, сцепленного с контуром.
– это изменение магнитного потока, сцепленного с контуром.
58. Электромагнитной индукцией называют явление возникновения электрического тока в замкнутом контуре при всяком изменении магнитного потока, пронизывающего контур.
Закон электромагнитной индукции Фарадея-Ленца. При всяком изменении магнитного потока через поверхность, ограниченную контуром, возникающая в контуре ЭДС индукции пропорциональна скорости изменения магнитного потока:
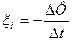
Направление индукционного тока определяется правилом Ленца: возникающий в замкнутом контуре индукционный ток имеет такое направление, что созданный им магнитный поток через поверхность, ограниченную контуром, стремится скомпенсировать то изменение внешнего магнитного потока, которым вызван этот ток
Если контур состоит из N последовательно соединенных витков, которые пронизываются одним и тем же потоком Ф, то ЭДС индукции в контуре равна:
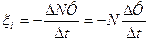
Индукционный ток в замкнутом контуре сопротивлением R при изменении магнитного потока на 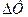 за время
за время 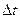 :
:
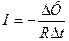
Заряд, который переносится индукционным током в замкнутом контуре сопротивлением R при изменении магнитного потока на 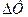 :
:
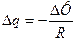
59.Самоиндукцией называется явление возникновения ЭДС индукции в замкнутом проводнике при изменении протекающего по нему тока
Если в процессе изменения силы тока контур не деформируется и магнитная проницаемость среды, в которой он находится, не меняется, то возникающая ЭДС самоиндукции равна:
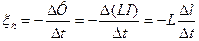
Энергия магнитного поля, создаваемого током I в проводнике с индукцией L:
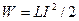
Индуктивность соленоида:

Где n – число витков на единицу длины, n=N/l, где N – число витков соленоида длиной l
60.Проводник, c протекающим по нему электрическим ток, всегда окружен магнитным полем, причем магнитное поле исчезает и появляется вместе с исчезновением и появлением тока. Магнитное поле, подобно электрическому, является носителем энергии. Логично предположить, что энергия магнитного поля совпадает с работой, затрачиваемой током на создание этого поля.
Рассмотрим контур индуктивностью L, по которому протекает ток I. С этим контуром сцеплен магнитный поток Ф=LI, поскольку индуктивность контура неизменна, то при изменении тока на dI магнитный поток изменяется на dФ=LdI. Но для изменения магнитного потока на величину dФ следует совершить работу dА=IdФ=LIdI. Тогда работа по созданию магнитного потока Ф равна
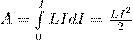
Энергию магнитного поля в катушке индуктивности можно найти по формуле:
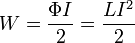
где:
Ф — магнитный поток,
I — ток,
L — индуктивность катушки или витка с током.
61. Закон полного тока это закон, связывающий циркуляцию вектора напряженности магнитного поля и ток.
Для описания поля в магнетиках часто пользуются величиной
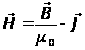 .
.
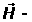 напряженность магнитного поля.
напряженность магнитного поля.
В вакууме вектор намагничения 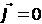 , поэтому
, поэтому 
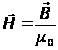 .
.
В магнетиках 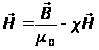 , или
, или  .
.
Величину 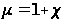 называют относительной магнитной проницаемостью вещества.
называют относительной магнитной проницаемостью вещества.
Следовательно, 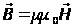 .
.
62. Первое М. у. имеет вид:
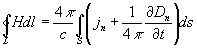
то есть циркуляция вектора напряжённости магнитного поля вдоль замкнутого контура L (сумма скалярных произведений вектора Н в данной точке контура на бесконечно малый отрезок dl контура) определяется полным током через произвольную поверхность S, ограниченную данным контуром. Здесь jn — проекция плотности тока проводимости j на нормаль к бесконечно малой площадке ds, являющейся частью поверхности S, 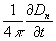 с = 3․1010 см/сек — постоянная, равная скорости распространения электромагнитных взаимодействий в вакууме.
с = 3․1010 см/сек — постоянная, равная скорости распространения электромагнитных взаимодействий в вакууме.
Бетатро́н — циклический ускоритель электронов с постоянной равновесной орбитой, ускорение в котором происходит с помощью вихревого электрического поля.
Согласно Максвеллу, если всякое переменное магнитное поле возбуждает в окружающем пространстве вихревое электрическое поле, то должно существовать и обратное явление: всякое изменение электрического поля должно вызывать появление в окружающем пространстве вихревого магнитного поля. Для установления количественных соотношений между изменяющимся электрическим полем и вызываемым им магнитным полем Максвелл ввел в рассмотрение так называемый ток смещения.
Второе М. у. является математической формулировкой закона электромагнитной индукции Фарадея (см. Индукция электромагнитная) записывается в виде:
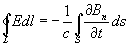
то есть циркуляция вектора напряжённости электрического поля вдоль замкнутого контура L (эдс индукции) определяется скоростью изменения потока вектора магнитной индукции через поверхность S, ограниченную данным контуром. Здесь Bn — проекция на нормаль к площадке ds вектора магнитной индукции В; знак минус соответствует Ленца правилу (См. Ленца правило) для направления индукционного тока.
64.
Уравне́ния Ма́ксвелла — система дифференциальных уравнений, описывающих электромагнитное поле и его связь с электрическими зарядами и токами в вакууме и сплошных средах.
Дата добавления: 2014-12-24; просмотров: 2025;
