Лекция № 6
«Хроматографический контроль технического состояния трансформаторов тяговых подстанций»
Показатели вычисляются по наработке:
Tn=T(1)+T(2)+...+T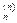 
,
где Т(i) - наработка между i-1 и i - тым отказом.
Возможно два пути оценки надежности ремонтируемых объектов: вычисление характеристик потока отказов и вычисление условных распределений наработки между отказами.
Рассмотрим путь оценки надежности вычислением характеристик
потока отказов.
Рассматриваются потоки случайных событий каждый из которых состоит в появлении отказов. Поток отказов может быть характерен
ведущей функцией потока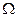 
(t) - это есть математическое ожидание числа отказов на интервале от 
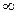до t.
Однако чаще всего используется параметр потока отказов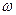 
(t) - плотность вероятности возникновения отказов ремонтируемых объектов, определяемая для расчетного момента суммарной наработки
Интенсивность потока событий определяется как дифференциал ведущей функции:
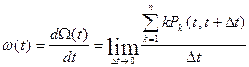
Параметр потока событий определяется:
a(t)=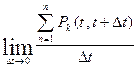 
,
где Pk(t,t+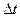 
) - вероятность появления к событий на интервале (t,t+ 
.
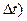Потоки отказов являются ординарными потоками , т.е. вероятность совмещения в один и тот же момент двух и более отказов ничтожно мала.
Таким образом: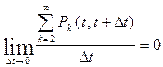 
.
Тогда интенсивность равна:
.
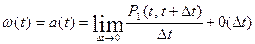P1(t,t+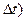 
- вероятность появления одного события на интервале (t,t+ .
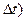0( 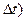- бесконечно мала величина на много меньше чем 
.
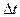Вероятность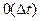 
- это есть вероятность одного и более отказов в один момент . Чтобы не смешивать с интенсивностью отказов неремонтируемых объектов принять используемый термин параметр потока отказов.
Рассматривают две математические модели случайных потоков отказов: без последействия и с ограниченным последействием.
1. Без последействия.
Вероятность отказов в 
любом интервале не зависит от отказов в других интервалах:
для ремонтируемых объектов -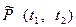 
.
Пуассоновский поток отказов: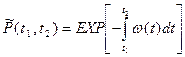 
Пуассоновский поток характерен для сложных не резервируемых систем, состоящих из высоконадежных элементов.
При стационарном потоке отказов: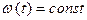 
, без последействия:
.
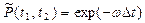2. С ограниченным последействием.
Когда нельзя допустить случай с последействием, тогда рассматривают потоки с ограниченным последействием. То есть вероятность появления отказов за наработку (t1,t2) зависит от наработки, накопленной от последнего отказа и не зависит от предыдущего.
Уравнение Вольтера второго порядка: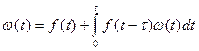 
.
Уравнение решается преобразованием Лапласа.
Если наработка между отказами имеет показательное распределение, то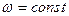 
, то есть:
f(t)=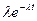 
, то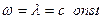 
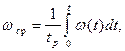где tp - технический ресурс.
Если при t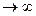 
плотность распределения наработки до отказа f(t) 
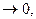то существует установившееся значении параметра потока отказов:
,
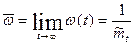где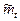 
- наработка на отказ ремонт объекта.
Наработка 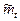- это отношение наработки ремонтируемого объекта к математическому ожиданию его отказов.
Дата добавления: 2014-12-24; просмотров: 1338;