О ДОКАЗАТЕЛЬСТВЕ, МЕТОДЕ И СИСТЕМЕ
Определение доказательства. Мы уже имели случай употреблять понятие доказательства в связи с понятием умозаключения. Теперь мы дадим его определение и укажем, какое существует различие между доказательством и умозаключением.
Мы видели, что суждения могут быть непосредственно очевидными, или они могут сделаться очевидными, если мы их сведём к положениям, которые имеют характер непосредственно очевидный. Если мы при помощи такого приема делаем суждения очевидными, то можно сказать, что мы их доказываем. Это приведение к очевидности облекается в силлогистическую форму, так что доказательство может быть определено как выведение какого-либо суждения из другихсуждений, признанных истинными и очевидными.
Таким образом, доказательство вообще имеет формулу силлогистического умозаключения, но есть существенные пункты отличия между умозаключением и доказательством.
Именно в умозаключении мы не всегда обращаем вниманиенато, истинны ли посылки; в доказательстве же истинность посылок является самым главным требованием. Кроме того, доказательство отличается от силлогизма ещё и тем, что в нём доказываемое суждение, соответствующее заключению силлогизма, известно заранее.
Во всяком доказательстве мы различаем три части: 1) доказываемое положение, или тезис; это именно то, что должно быть доказано или сделано очевидным; 2) основы доказательства, или аргументы; это то, при помощи чего тезис доказывается или делается очевидным; 3) форма доказательства, или способ, каким тезис выводится из аргументов. Тезис доказательства соответствует заключению в силлогизме. Аргументы соответствуют посылкам силлогизма. Форма доказательства есть логическая схема, при помощи которой выводится заключение. Например, нужно доказать, что «железо плавко». Это есть тезис. Для доказательства нам необходимо воспользоваться следующими двумя аргументами; «все металлы плавки», «железо есть металл». Построив силлогизм, мы докажем наш тезис.
Основные принципы и аксиомы. Мы видим, таким образом, что Доказательство сводится к раскрытию очевидности данного суждения из очевидности других суждений, которые называются аргументами. А если эти последние не очевидны, то как поступить в таком случае? Нужно доказать их в свою очередь при помощи каких-либо других аргументов. Но так как эти последние также могут быть сомнительными, то доказательство большей частью представляет целую цепь умозаключений. В конце концов всякое доказательство должно приводить к таким положениям, которые имеют уже бесспорный или очевидный характер. Эти последние или сутьаксиомы, или это суть общепризнанные общие положения, которые в таком случае называютсяосновными принципами.
Прямое и косвенное доказательство. Процесс доказательства может быть прямой или косвенный. В прямом доказательстве мы выводим истинность тезиса из истинности аргументов при помощи умозаключения; непрямое, или апагогическое, доказательство выводит истинность тезиса из невозможности допустить или признать истинность положения, противоречащего тезису. Именно, в непрямом доказательстве мы берём положение, противоречащее тезису, и предполагаем его истинным (такое положение называется антитезисом). Затем из этого положения выводим следствия, которые приводят к противоречию с данными или признанными положениями. Вследствие этого нам приходится отвергнуть истинность противоречащего положения, которое мы предположительно допустили, а отсюда будет следовать истинность тезиса. Таким образом доказывается тезис.
Возьмём пример из математики. Требуется доказать, что в треугольнике, в котором два угла равны, противолежащие им стороны также равны. Пусть в треугольнике АВС угол а равняется углу b, и пусть противолежащие им стороны будут АС и ВС. Нам нужно доказать, что АС == ВС. Это есть тезис. Возьмём положение, противоречащее тезису: «АС не равняется ВС». Это будет антитезис; тогда из этого последнего положения (согласно теореме, что во всяком треугольнике против большего угла лежит большая сторона) будет следовать, что угол а должен быть или больше, или меньше угла b. Но так как этот, вывод противоречит принятому нами положению, то антитезис, является ложным; тогда истинным должно быть положение, противоречащее ему, именно тезис. Такого рода доказательство называется также reductio ad impossibile или reductio adabsurdum.
Понятие о методе и системе. Для достижения определённых целей в процессе мышления те или другие суждения или ряд суждений должны располагаться в определённом порядке, сообразно известным правилам. Этотпорядок расположения суждений, способствующий достижению определённой цели, называется методом. Как мы уже видели, для того, чтобы доказать существование причинной связи между явлениями, нужно, чтобы наши суждения располагались в том или другом порядке: или по методу сходства, или по методу разницы и т. п. Понятие «метод» употребляется и по отношению к физическим процессам. Например, можно учиться плавать, руководясь определёнными правилами, — это будет методическое обучение. Но можно учиться без всяких правил—это будет неметодическое обучение.
Системой вообще мы называем соединение взаимосвязанных явлений в одно целое. Суждения, конечно, тоже могут соединяться таким образом, чтобы составлять одно целое; тогда они образуют «систему» суждений. Система суждений составляет науку.Наука, таким образом,есть совокупность систематически расположенных суждений достоверных, или по крайней мере вероятных.
Научное мышление должно осуществляться сообразно с известными правилами, т.е. по определённому методу. В научном мышлении метод может применяться в двух различных случаях, именно: во-первых, воткрытии новых истин и, во-вторых, в определённомрасположении уже открытых истин, как это бывает визложении научных данных для наиболее ясного их понимания. И для открытия и для изложения научных истин служат методы аналитический и синтетический.
Анализ и синтез. Для того чтобы понять, в чём заключаются эти методы, заметим, что частное положение, вывод, следствие находится в таком же отношении к общему положению, принципу, основанию, в каком действие находится к причине. Как из известной причины получается известное действие, так из известного принципа, основания получается известный вывод, следствие. Мы так же ищем для известного положения принцип или основание, как для известного действия ищем его причину. С другой стороны, как для известной причины мы ищем её действие, так для известных принципов мы можем искать их следствия.
Отсюда, в зависимости от того, что мы ищем, получаются два различных процесса.
Если мы от причины идём к действию, от основания к выводу, То такой путь называетсяпрогрессивным илисинтетическим.Прогрессивным он называется потому, что он соответствует реальному ходу природы, действительному ходу вещей, так как в природе причина раньше, чем действие. Обратный путь, именно от действия к причине, от выводов к принципам, называетсярегрессивным, аналитическим.
Схема отношения между анализом и синтезом:
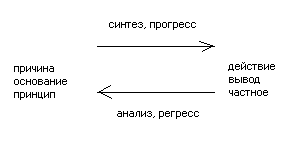
Часто словам «анализ» и «синтез» придают другое значение, именно под анализом понимают метод разложения целого на его составные части, а под синтезом.—обратный метод сложения целого и в его частей, или элементов. В этом смысле чаще всего говорят об анализе и синтезе химическом. Но для того чтобы истинный смысл понятий «анализ» и «синтез», как они употребляются в научном исследовании и изложении, был ясен, нужно считать основным значением слова «анализ» то, которое мы только что указали, именно сведение частных положений к основным принципам, а под синтезом следует понимать выведение следствий из основных принципов .
Аналитический метод исследования мы употребляем тогда, когда мы ищем причины данных действий. Судья, моралист и др., которые ищут причины известных действий, употребляют метод аналитический; законодатель, политик, педагог, которые стараются предусмотреть действия известных причин, должны идти путём синтетическим.
Для объяснения применения анализа возьмём следующий пример. Чтобы решить задачу вписывания правильного шестиугольника в данный круг, мы рассуждаем так. Предположим, что задача решена, и пусть АВ будет одной из сторон вписанного шестиугольника. Если мы проведём радиусы к конечным точкам сторон, то треугольник, образовавшийся таким образом, будет равноугольный (так как каждый угол равен двум третям прямого угла); следовательно, сторона вписанного правильного шестиугольника равна радиусу. Отсюда следует, что, для того чтобы вписать правильный шестиугольник в данный круг, нужно радиус нанести шесть раз на окружность. Здесь применение аналитического метода очевидно. Мы, сделав предположение, что задача решена, т. е. допустив данное частное положение, нашли то условие, тот общий принцип, при котором это частное положение возможно, т. е. из которого это положение можно вывести. Другими словами, мы данное частное положение сводим к общему принципу.
Примером применения синтеза может служить теорема: «во всяком треугольнике сумма его углов равняется двум прямым углам». Для доказательства этой теоремы мы должны принять следующих два общих положения: «внутренние накрест лежащие углы равны» и «всякая пара смежных углов равна двум прямым». Из этих общих положений мы выводим искомое положение.
Отношение анализа и синтеза к индукции и дедукции. Но, спрашивается, в каком отношении находятся методы аналитический и синтетический к методам индуктивному и дедуктивному? Отношение между ними таково, что анализ соответствует индукции, а синтез соответствует дедукции. Что анализ соответствует индукции, легко пояснить следующим образом.
Индукция имеет целью открытие законов, общих принципов. В процессе индукции мы идём от частных положений к общим принципам. Поэтому в процессе индукции мы совершаем регрессивный путь. Из этого следует, что индукция соответствует анализу.
Наоборот, дедукция выводит из общих принципов частные положения, те или иные следствия. Из этого становится ясным родство дедуктивного метода с синтетическим. Синтетический метод состоит в том, что мы предполагаем известные принципы открытыми и доказанными; из этих общих принципов мы выводим следствия.
Вопросы для повторения
Что такое доказательство и чем оно отличается от силлогизма? Какие три части отличаем мы в доказательстве? Что такое основные принципы? Какое доказательство называется прямым? Какое доказательство называется косвенным? Изложите ход косвенного доказательства. Что называется методом? Что называется системой?. В каких двух случаях употребляется метод в научном мышлении? Какой метод называется аналитическим и какой синтетическим? Почему синтетический метод называется прогрессивным, а аналитический регрессивным? Покажите применение методов аналитического н синтетического в математике. Какое существует отношение между методами аналитическим и синтетическим и методами индуктивным и дедуктивным?
Глава XXVI
Дата добавления: 2014-12-24; просмотров: 900;
