Осындылағыш
Логикалық схемаларда қолданылатын екілік сандарды қосу, көбейту амалдары жиі қарастырылады. Екілік санды қосу тасымалдау есебімен сәйкес разрядтарды қосуға әкеледі.
Екі екілік санды қосуды жүзеге асыратын логикалық элементтердің шартты графикалық бейнеленуімен шындық кестесін (3.8-кесте) қарастыралық.
| А | В | Σ | С0 |
| Екілік сан қосылғыш тар | қосынды | тасымал | |
| шектеулі НЕМЕСЕ | ЖӘНЕ |
3.8-кесте. Жартылай қосындылағыш шындық кестесі
мұндағы, А, В - кіріс сигналдары, Σ – қосынды, С0 – шығыс тасымал дегенді білдіреді.
Бұл кестеден С0 =А*В екенін көреміз. Мұндай талап етілетін логикалық деңгейді алу үшін ЖӘНЕ элементін пайдалануға болады. Ал, енді қосынды шығысындағы күйді бульдік өрнекпен сипаттауға тырысалық. Сонда Σ=А*В+В*А бұл өрнек үшін 2 ЖӘНЕ-ЕМЕС 1 НЕМЕСЕ логикалық элементтері пайдаланылады, яғни, шектеулі НЕМЕСЕ пайдаланылады. Σ=А||В.
Сонымен, шектеулі НЕМЕСЕ салыстыру схемасы ғана емес, оның басқа маңыздылығы да бар. Ол оның шындық кестесін екілік сандарды қосу кестесімен салыстырудан шығады. Мұнда тек жоғары разрядқа көшу қарастырылмайды, оны қалыптастыру үшін салыстыру схемасына (шектеулі немесе) сәйкестендіру схемасын (және) қосу керек. Соңғысы А және В аргументтерінің екеуінің де мәндері бір мезгілде 1 болғанда ғана логикалық бірлікті туғызады. Шыққан схема жартылай қосындылағышдеп аталады.
Толық қосындылағыш үш кіріске ие. Көп разрядты екілік сандарды қосу үшін бірнеше жартылай және толық қосындылағыштар қажет. Мысалы, үш разрядты параллель қосындылағыш. Мысал ретінде тізбектелген әрекеттер қосындылағышын қарастырамыз.

Cік S
А C0
В
3.10-сурет.Қосындылағыш
Мұның барлық мүмкін екілік разрядты А,В,Сік (cаrry input) қосылғыштары комбинациясы үшін шындық кестесі:
3.9-кесте. Қосындылағыш шындық кестесі
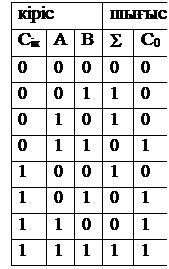
Дата добавления: 2014-12-22; просмотров: 2618;
