Англо-американская система мер

Наблюдатель, находясь в море, всегда видит вокруг себя определенный участок земной поверхности, в центре которого находится он сам. Этот участок принято называть кругозором наблюдателя. Границей кругозора наблюдателя является линия, по которой небосвод как бы соприкасается с морем; называется она линией видимого горизонта. С увеличением высоты глаза наблюдателя его кругозор расширяется, линия видимого горизонта отодвигается от наблюдателя, дальность видимого горизонта увеличивается.
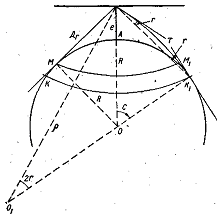
На сферической поверхности Земли линия видимого горизонта представляется малым кругом ММ1 (смотрите рисунок), по которому прямые линии — лучи, проведенные во все стороны от глаза наблюдателя, касаются земной поверхности.
Геометрическая дальность видимого горизонта Дг без учета земной рефракции, представляющая собой сферический радиус AM, может быть рассчитана на основании следующих соображений. Учитывая, что высота глаза наблюдателя е по сравнению с размерами Земли незначительна (на современных кораблях высота глаза едва ли может быть больше 50 м), сферический радиус AM можно считать равным длине касательной ВМ. Тогда из прямоугольного треугольника ОВМ можно написать

Дг = ВМ = √ {(R + t)² - R²};

Дг = √ {2Re + R² - R²} = √ {2Re (1 + e/2R)}.

Oтношение e / 2R настолько мало, что пренебрежение им практически не скажется на, точности вычисляемой дальности. Учитывая это, можно считать, что

Дг = √ {2Re}

Длину сферического радиуса AM и приравненной к нему касательной ВМ мы назвали геометрической дальностью видимого горизонта без учета земной рефракции.

Если бы земная атмосфера во всех своих слоях имела одинаковую плотность (или будь Земля вовсе лишена атмосферы), лучи света от линии видимого горизонта MM1 достигали бы глаза наблюдателя по прямым без искривлений и сферический радиус AM представлял бы фактическую дальность видимого горизонта. В действительности же в земной атмосфере лучи света распространяются не прямолинейно, а с некоторым преломлением вследствие неодинаковой плотности атмосферы в разных ее слоях. Явление преломления светового луча, проходящего через слои земной атмосферы с разной плотностью, называется земной рефракцией. Вследствие рефракции траектория луча, соединяющего малый круг ММ1 с глазом наблюдателя В, в действительности будет кривой линией, обращенной вогнутостью к Земле. Точка касания этого луча с поверхностью Земли будет лежать несколько дальше точки М1, а именно в точке К1. Следовательно, кругозор наблюдателя за счет рефракции расширится и дальность видимого им горизонта увеличится.
Земная рефракция характеризуется углом r земной рефракции, заключенным между хордой ВК1 и касательной к траектории светового луча K1B в точке В. Величина этого угла зависит от преломляющих свойств атмосферы в момент наблюдений, в свою очередь зависящих от разности температуры воды и воздуха, влажности воздуха, атмосферного давления и других факторов. Проходя из более плотных слоев атмосферы у поверхности Земли в менее плотные, на высоте е луч света, преломляясь, искривляется и принимает вид кривой К1В. Поэтому наблюдатель видит точку К1 не по направлению касательной BM1 или хорды BK1, а по направлению касательной ВТ к траектории действительного луча К1В. На сравнительно небольших расстояниях от точки В траекторию луча света можно принять за дугу окружности радиуса ρ . Из многочисленных наблюдений, произведенных в разное время и в разных частях земного шара, установлено, что отношение R / ρ, называемое коэффициентом земной рефракции, при нормальном состоянии атмосферы примерно равно 0,16. Этот коэффициент характеризует преломляющую способность земной атмосферы.
Для отыскания зависимости геометрической дальности видимого горизонта с учетом земной рефракции от высоты глаза наблюдателя е обратимся к рисунку. На этом рисунке действительная дальность видимого горизонта Де представлена сферическим радиусом ВК1 малого круга КК1. Вследствие малости кривизны земной поверхности, а тем более зрительного луча практически можно за дальность видимого горизонта принимать как длину сферического радиуса АК1, так и длину хорды ВК1, а также и сферический радиус ВК1. В треугольнике ОК1В угол ВК1О равен 90 градусов минус r, угол К1ВО равен 90 градусов минус (с-r), ВК1 = Де - геометрическая дальность видимого горизонта с учетом земной рефракции.
Применяя к треугольнику ОК1В теорему синусов, можно написать:
ОВ / sin (90° - r) = ОК₁ / sin {90° - (c-r)}
или
R+e / R = cos r / cos (c-r)

Вычтя из правой и левой частей полученного равенства по единице
R+e / R - 1 = cos r / cos (c-r) - 1,
получим
R + e - R / R = cos r - cos (c-r) / cos (c-r);

e / R = cos r - cos (c-r) / cos (c-r).

Заменив в правой части разность косинусов на удвоенное произведение синуса полусуммы на синус полуразности, получим

e / R = 2 sin c/2 sin {c-2r/2} / cos (c-r)

По малости углов с и r разложим в ряд sin c/2, sin {(c-2r/2} и cos (c-r), ограничившись при этом первыми членами разложения:

sin (c/2) = c/2; sin {c-2r/2}=c-2r/2; cos (c-r)=1.

Подставляя в предыдущую формулу результаты разложения, найдем

e/r = 2 * c/2(c-2r/2) = c(c-2r)/2

Но c=Д_е/R, а 2r=Д_e / ρ = Д_еR / Rρ = (Д_е / R) * k, где
k = R / ρ - коэффициент земной рефракции.

С учетом последних замечаний

e/R=Д_е/2R(Д_е/R - kД_е/R) = Д_е²/2R²*(1-k),
откуда
Д_е² = (2R² * е) / R(1-k);
Д_е² = 2Re / (1-k)
и
Д_е = √ {2Re/1-k} = (1-k)-½ * √ {2Re}.

Разложив (1-к) в минус 1/2 степени в ряд и ограничившись двумя первыми членами разложения, получим
Д_е = (1+к/2)* √ {2Re}
или
Д_е (мили) = 1,08 * √ {2*6371*е (м) / 1852 * 1852} = 2,08 √ е (м).