СТРУКТУРА ДАП

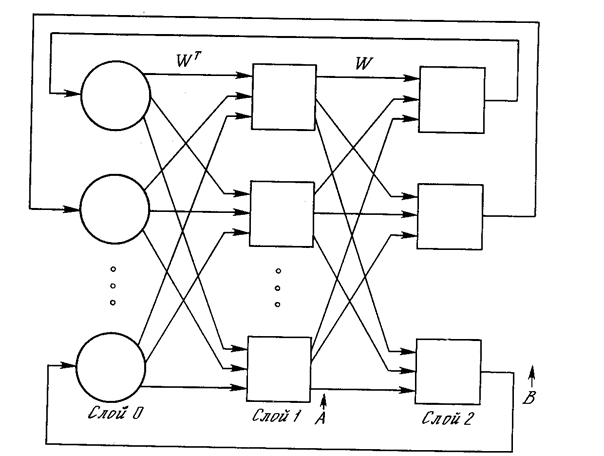
Рис. 7.1. Конфигурация двунаправленной ассоциативной памяти

На рис. 7.1 приведена базовая конфигурация ДАП. Эта конфигурация существенно отличается от используемой в работе [9]. Она выбрана таким образом, чтобы подчеркнуть сходство с сетями Хопфилда и предусмотреть увеличения количества слоев. На рис. 7.1 входной вектор А обрабатывается матрицей весов W сети, в результате чего вырабатывается вектор выходных сигналов нейронов В. Вектор В затем обрабатывается транспонированной матрицей Wtвесов сети, которая вырабатывает новые выходные сигналы, представляющие собой новый входной вектор А. Этот процесс повторяется до тех пор, пока сеть не достигнет стабильного состояния, в котором ни вектор А, ни вектор В не изменяются. Заметим, что нейроны в слоях 1 и 2 функционируют, как и в других парадигмах, вычисляя сумму взвешенных входов и вычисляя по ней значение функции активации F. Этот процесс может быть выражен следующим образом:

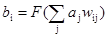(7.1)

или в векторной форме:

В = F(AW), (7.2)

где В – вектор выходных сигналов нейронов слоя 2, А – вектор выходных сигналов нейронов слоя 1, W – матрица весов связей между слоями 1 и 2, F – функция активации.

Аналогично

A = F(BWt) (7.3)

где Wtявляется транспозицией матрицы W.

Как отмечено в гл. 1, Гроссберг показал преимущества использования сигмоидальной (логистической) функции активации

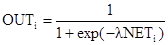(7.3)

где OUT_i – выход нейрона i, NET_i – взвешенная сумма входных сигналов нейрона i, l – константа, определяющая степень кривизны.

В простейших версиях ДАП значение константы l выбирается большим, в результате чего функция активации приближается к простой пороговой функции. В дальнейших рассуждениях будем предполагать, что используется пороговая функция активации.

Примем также, что существует память внутри каждого нейрона в слоях 1 и 2 и что выходные сигналы нейронов изменяются одновременно с каждым тактом синхронизации, оставаясь постоянными между этими тактами. Таким образом, поведение нейронов может быть описано следующими правилами:

OUT_i(n+1) = 1, если NET_i(n)>0,

OUT_i(n+l) = 0, если NET_i(n)<0,

OUT_i(n+l) = OUT(n), если NET_i(n) = 0,

где OUT_i(n) представляет собой величину выходного сигнала нейрона i в момент времени п.

Заметим, что как и в описанных ранее сетях слой 0 не производит вычислений и не имеет памяти; он является только средством распределения выходных сигналов слоя 2 к элементам матрицы Wt.