Задача коммивояжера
Задача коммивояжера является оптимизационной задачей, часто возникающей на практике. Она может быть сформулирована следующим образом: для некоторой группы городов с заданными расстояниями между ними требуется найти кратчайший маршрут с посещением каждого города один раз и с возвращением в исходную точку. Было доказано, что эта задача принадлежит большому множеству задач, называемых «NP-полными» (недетерминистски полиномиальными) [З]. Для NP-полных задач не известно лучшего метода решения, чем полный перебор всех возможных вариантов, и, по мнению большинства математиков, маловероятно, чтобы лучший метод был когда либо найден. Так как такой полный поиск практически неосуществим для большого числа городов, то эвристические методы используются для нахождения приемлемых, хотя и неоптимальных решений.
Описанное в работе [8] решение, основанное на сетях с обратными связями, является типичным в этом отношении. Все же ответ получается так быстро, что в определенных случаях метод может оказаться полезным.
Допустим, что города, которые необходимо посетить, помечены буквами A, B, C и D, а расстояния между парами городов есть dab, dbc и т. д.
Решением является упорядоченное множество из n городов. Задача состоит в отображении его в вычислительную сеть с использованием нейронов в режиме с большой крутизной характеристики (l приближается к бесконечности). Каждый город представлен строкой из n нейронов. Выход одного и только одного нейрона из них равен единице (все остальные равны нулю). Этот равный единице выход нейрона показывает порядковый номер, в котором данный город посещается при обходе. На рис. 6.6 показан случай, когда город C посещается первым, город A – вторым, город D – третьим и город B – четвертым. Для такого представления требуется п2 нейронов – число, которое быстро растет с увеличением числа городов. Длина такого маршрута была бы равна dca + dad + ddb + dbc. Так как каждый город посещается только один раз и в каждый момент посещается лишь один город, то в каждой строке и в каждом столбце имеется по одной единице. Для задачи с п городами всего имеется п! различных маршрутов обхода. Если п = 60, то имеется 6934155х1078 возможных маршрутов. Если принять во внимание, что в нашей галактике (Млечном Пути) имеется лишь 1011 звезд, то станет ясным, что полный перебор всех возможных маршрутов для 1000 городов даже на самом быстром в мире компьютере займет время, сравнимое с геологической эпохой.
Продемонстрируем теперь, как сконструировать сеть для решения этой NP-полной проблемы. Каждый нейрон снабжен двумя индексами, которые соответствуют городу и порядковому номеру его посещения в маршруте. Например, OUTxj = 1 показывает, что город х был j-ым по порядку городом маршрута.
Функция энергии должна удовлетворять двум требованиям: во-первых, должна быть малой только для тех решений, которые имеют по одной единице в каждой строке и в каждом столбце; во-вторых, должна оказывать предпочтение решениям с короткой длиной маршрута.
Первое требование удовлетворяется введением следующей, состоящей из трех сумм, функции энергии:
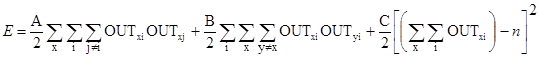 , (6.9)
, (6.9)
где A, B и C – некоторые константы. Этим достигается выполнение следующих условий:
1. Первая тройная сумма равна нулю в том и только в том случае, если каждая строка (город) содержит не более одной единицы.
2. Вторая тройная сумма равна нулю в том и только в том случае, если каждый столбец (порядковый номер посещения) содержит не более одной единицы.
3. Третья сумма равна нулю в том и только в том случае, если матрица содержит ровно п единиц.
| город | Порядок следования | |||
| A | ||||
| B | ||||
| C | ||||
| D |
Рис. 6.6. Маршрут коммивояжера
Второе требование – предпочтение коротким маршрутам – удовлетворяется с помощью добавления следующего члена к функции энергии:
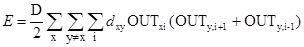 , (6.10)
, (6.10)
Заметим, что этот член представляет собой длину любого допустимого маршрута. Для удобства индексы определяются по модулю n, т. е. OUTn+j = OUTj, a D – некоторая константа.
При достаточно больших значениях A, B и C низкоэнергетические состояния будут представлять допустимые маршруты, а большие значения D гарантируют, что будет найден короткий маршрут.
Теперь зададим значения весов, т. е. установим соответствие между членами в функции энергии и членами общей формы (см. уравнение 6.2)).
Получаем
wxi,yi = –Aδxy(1 – δij) (не допускает более одной единицы в строке)
–Bδij(1 – δxy) (не допускает более одной единицы в столбце)
–С (глобальное ограничение)
–Ddxy(δj,i+1 + δj,i-1) (член, отвечающий за длину цикла),
где δij = 1, если i = j, в противном случае δij = 0. Кроме того, каждый нейрон имеет смещающий вес хi, соединенный с +1 и равный Сп.
В работе [8] сообщается об эксперименте, в котором задача коммивояжера была решена для 10 городов. В этом случае возбуждающая функция была равна
OUT = ½ [1 + th(NET/U0)].
Как показали результаты, 16 из 20 прогонов сошлись к допустимому маршруту и около 50% решений оказались кратчайшими маршрутами, как это было установлено с помощью полного перебора. Этот результат станет более впечатляющим, если осознать, что имеется 181440 допустимых маршрутов.
Сообщалось, что сходимость решений, полученных по методу Хопфилда для задачи коммивояжера, в сильной степени зависит от коэффициентов, и не имеется систематического метода определения их значений [11]. В этой работе предложена другая функция энергии с единственным коэффициентом, значение которого легко определяется. В дополнение предложен новый сходящийся алгоритм. Можно ожидать, что новые более совершенные методы будут разрабатываться, так как полностью удовлетворительное решение нашло бы массу применений.
Дата добавления: 2014-12-22; просмотров: 773;
