Экспоненциальный закон распределения.

Экспоненциальное (показательное) распределение -это распределение вероятностей, которое описывается дифференциальной функцией.

Экспоненциальное распределение определяется одним параметром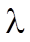

Вопрос 6 Функция распределения. Плотность вероятности. Стандартные интервалы.

Функция распределения = интегральная функция распределения – это вероятность того, что случайная величина Х примет значение меньше некоторого наперед заданного числа х- малое:

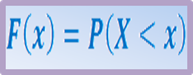
Свойства:

1)

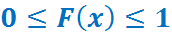
2)

Для дискретных случайных величин а)

Для непрерывных случайных величин б)

а) б)

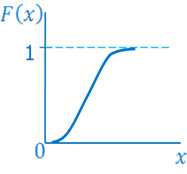
Плотность распределения вероятностей, илиплотность распределения непрерывнойслучайной величины Х=дифференциальная функция распределения-производная ее функции распределения.

Свойства плотности вероятности:

1. Неотрицательная функция

2. Площадь фигуры, ограниченной кривой распределения и осью абсцисс, равна единице.

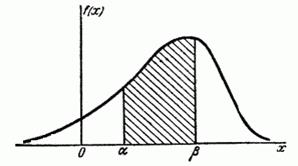
3. Вероятность попадания непрерывной случайной величины в интервал [а,b] равна определенному интегралу от ее плотности вероятности в пределах от a до b.