Статистическое определение вероятности.

Основным методом каменной кладки в многоэтажных кар­касных зданиях является поточный,в основу которого положе­ны следующие принципы:

• выполнение всего комплекса работ по захватно-ярусной системе;

• разделение комплексного процесса кладки на составляю­щие процессы с собственными специализированными звеньями;

• последовательное по захваткам и ярусам выполнение про­цессов в одинаковом темпе специализированными звеньями постоянного состава;

• переход звеньев с захватки на захватку через равные про­межутки времени, называемые шагом потока;

• обязательная увязка продолжительности монтажа и камен­ной кладки на захватке.

Процесс возведения многоэтажного кирпичного дома обыч­но осуществляет комплексная бригада. Количественный и ква­лификационный состав бригады определяется в зависимости от фронта работ, сроков строительства, принятых методов произ­водства работ, производительности рабочих и машин.
Комплексная бригадасостоит из звеньев монтажников, ка­менщиков, плотников, такелажников, транспортных рабочих. Ведущим в бригаде является звено монтажников или камен­щиков, состав звеньев других специальностей комплектуется с учетом обеспечения ими нормальной работы ведущего звена. Численность комплексной бригады может изменяться от 20 до 40 человек в зависимости от конструктивных особенностей здания и особенно кладки.

При поточном выполнении каменной кладки основные по­нятия технологии работ имеют свое специфическое определение.

Захватка— типовая, повторяющаяся в плане часть здания с приблизительно равными на данном и последующих за ним участках (полсекции, секция, две секции) объемами кладки, предоставленная бригаде каменщиков для поточного выполне­ния работы на целое число смен.

Делянка— кратная часть захватки, отводимая звену камен­щиков для бесперебойной работы в течение нескольких смен.

Ярус— часть здания, условно ограниченная по высоте, где без изменения уровня работы каменщиков по отношению к перекрытию выполняют рабочие процессы кладки в течение одной смены.

Делянка, в зависимости от высоты этажа и тол­щины стен, по высоте может быть разбита на 2...3 яруса.

Число делянок и их размеры устанавливают в зависимости от трудоемкости кладки и сменной выработки звеньев. На сте­нах с простой кладкой в два кирпича при звене «двойка» длина делянки составит 12...17 м, для звена «тройка» — 19...25 м и для звена «пятерка» — 24...40 м.

Оптимальный для работы уровень кладки 60...80 см, произ­водительность труда падает до 50% при нулевом уровне и высо­те 1,1...1,2 м, поэтому именно в этих пределах и назначают вы­соту яруса. При высоте этажа до 2,8 м и толщине стен до двух кирпичей допускается иметь высоту яруса до 1,5 м, т. е. на эта­же два яруса по высоте, при большей толщине стен и высоте этажей более 3 м принимают три яруса. Кладку выполняют с многорядной или однорядной перевязкой, узкие простенки и столбы выкладывают по четырехрядной системе перевязки. Кладку первого яруса каменщики выполняют с земли или меж­дуэтажного перекрытия, второго и третьего с подмостей, раз­движных или устанавливаемых в два яруса. При свободной кладке свыше 4 м обычно используют трубчатые леса.

Комплектация звеньев каменщиков зависит от конструк­ции, толщины и сложности кладки, общего объема и трудоемкости работ, задействованного числа единиц монтажных меха­низмов.

Статистическое определение вероятности.

1) Вероятность события- число, относительно которого группируются значения частоты данного события в различных сериях большого числа испытаний

2) Относительная частота события-это доля тех фактически проведенных испытаний, в которых событие А появилось.

Это опытная экспериментальная характеристика, где m- число опытов, в которых появилось событие А; n- число всех проведенных опытов.

Если классическое определение вероятности осуществляется до опыта, то статистическое после опыта по результатам.

Вопрос 2 Понятие о совместных и несовместных событиях, зависимых и независимых.

Случайные события А1, А2,..Аn называются:

Совместные - если появление одного из них не исключает появления другого в одном и том же испытании.

Несовместные - если наступление одного события исключает появление другого.

Зависимое событие: вероятность появления одного из них зависит от появления другого.

Независимое событие: если вероятность появления одного из них не зависит от появления или не появления другого.

Условная вероятность события B- вероятность события B, найденная при условии, что событие A произошло. P(B/A)

Вопрос 3 Теоремы умножения и сложения вероятностей.

Сумма двух событий- это такое событие, при котором происходит хотя бы одно из этих событий (А или В).

Вероятность суммы:

Несовместных событий означает наступление или события А или события В и равна сумме вероятностей этих событий: P(A+B)= P(A) + P(B).

Совместных событий обозначает наступление события А или события В, или обоих событий вместе и равна сумме вероятностей этих событий без вероятности их совместного появления: P(A+B)= P(A) + P(B) – P(AB)

Теорема умножения вероятностей.

Произведение двух событий- это событие, состоящее в совместном появлении этих событий (А и В).

Вероятность совместного появления:

Независимых событий равна произведению вероятностей появления каждого из них: P(A*B)=P(A)*P(B)

Зависимыхсобытий: P(A*B)=P(A)*P(B/A)

Вопрос 4 Распределение дискретных и непрерывных случайных величин. Их характеристики: математическое ожидание, дисперсия, среднее квадратическое отклонение.

Случайная величина - это величина, которая в результате испытания примет одно и только одно возможное значение заранее неизвестное.

Случайные величины: дискретные (счет: 1-2-3..) и непрерывные (измерения: Амперы, Вольты..)

Дискретная случайная величина- случайная величина, когда принимает отдельное изолированное, счетное множество значений.

Непрерывная случайная величина- случайная величина, принимающая любые значения из некоторого интервала.

Распределение= закон распределения - это совокупность значений случайной величины и вероятностей их появления.

Способы задания величин: табличный (дискретные), аналитический, графический.

Характеристики:

Математическое ожидание - сумма произведений случайных величин на вероятность их появления.

Для дискретных случайных величин: а)

Для непрерывных случайных величин: б)

а) 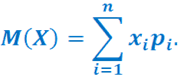б)

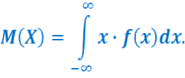
Дисперсия - рассеяние вокруг математического ожидания.

Для дискретных случайных величин: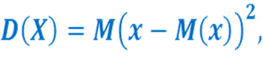

Для непрерывных случайных величин:

Среднее квадратическое отклонение случайной величины- корень квадратичный из дисперсии.

Стандартное отклонение

Вопрос 5. Нормальный и экспоненциальный законы распределения неперывных случайных величин.

Нормальный закон распределения (НРЗ) = Закон Гусса -распределение вероятностей непрерывной случайной величины, которое описывается дифференциальной функцией.

Непрерывная случайная величина X имеет нормальный закон распределения, если ее плотность вероятности имеет вид:

Свойства плотности распределения вероятностей:

1) Она колоколообразная ("колокол Гаусса").

2) Плотность определяется двумя параметрами: математическим ожиданием (µ) и средним квадратическим отклонением (σ).

3) Кривая сдвигается вправо, если среднее увеличивается при постоянном квадратическом отклонении, и сдвигается влево, если среднее уменьшается.

4) Кривая расширяется, если среднее квадратическое отклонение σ увеличивается (если среднее постоянно).

5) Кривая становится более остроконечной с меньшей шириной основания колокола, если σ уменьшается при среднем постоянном (площадь под графиком всегда равна 1) (рис.в).

Рис. Кривая нормального закона распределения и ее изменение при изменении параметров

Дополнительные свойства:

«Правило трех сигм»

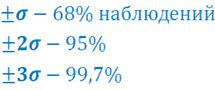
Вероятность того, что нормально распределенная случайная величина X находится между (µ-σ) и (µ+σ), равна 0,68, т.е. 68% случайной величины X отличается от среднего не более чем на одно стандартное отклонение ±σ.

Вероятность того, что нормально распределенная случайная величина X находится между (µ-2σ) и (µ+2σ), равна 0,95, т.е. примерно 95% случайной величины X отличается от среднего на два стандартных отклонения ±2σ.

Вероятность того, что нормально распределенная случайная величина X находится между (µ-3σ) и (µ+3σ), равна 0,99, т.е. 99% (практически достоверно). Это свойство носит название правило трех сигм