Законы Ньютона
Это опытные законы и теоретически не доказаны. Но три закона Ньютона являются системой взаимосвязанных законов, которые играют исключительную роль в механике. Законы открыты в 1867 году и являются обобщением результатов огромного человеческого опыта.
4.1. Первый закон Ньютона (закон инерции)
 Всякое тело находится в состоянии покоя или равномерного прямолинейного движения, пока воздействие со стороны других тел не заставит его изменить это состояние.
Всякое тело находится в состоянии покоя или равномерного прямолинейного движения, пока воздействие со стороны других тел не заставит его изменить это состояние.
И состояние покоя и равномерное прямолинейное движение свидетельствуют об отсутствии ускорения, поэтому первый закон Ньютона можно сформулировать в следующем виде:
 Скорость тела не меняется, если на него не действуют другие тела.
Скорость тела не меняется, если на него не действуют другие тела.
Первый закон Ньютона выполняется лишь в инерциальных системах отсчета. Сам закон называют иногда законом инерции.
Опытным путем установлено, что инерциальной можно считать гелиоцентрическую систему отсчета – звездная система с началом координат в центре Солнца.
Системы отсчета, связанные с Землей, строго говоря, неинерциальны, т.к. Земля вертится вокруг своей оси и вокруг Солнца. Этим обусловлено наличие ускорений земных систем отсчета.
Однако эти ускорения достаточно малы, и для решения многих практических задач ими можно пренебречь. В этих случаях системы координат, связанные с Землей, можно считать инерциальными. (Вспомним, что законы Ньютона открыты на основании опытных данных и опыты эти проводились на Земле.)
4.2. Второй закон Ньютона(основной закон динамики)
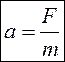
 Ускорение, приобретаемое телом, прямо пропорционально вызывающей его силе, совпадает с нею по направлению и обратно пропорционально массе тела.
Ускорение, приобретаемое телом, прямо пропорционально вызывающей его силе, совпадает с нею по направлению и обратно пропорционально массе тела.
или сила, как производная импульса:
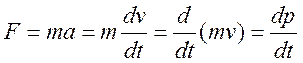 ,
,
где 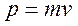 – импульс тела.
– импульс тела.
Более общая формулировка второго закона Ньютона:
Скорость изменения импульса материальной точки равна действующей на нее силе.
Второй закон Ньютона справедлив только в инерциальных системах отсчета.
Принцип независимости действия сил:
Если на материальную точку действует одновременно несколько сил, то каждая из этих сил сообщает материальной точке ускорение согласно второму закону Ньютона, как будто других сил не было.
Согласно этому принципу, силы и ускорения можно разлагать на составляющие, использование которых приводит к существенному упрощению решения задач.
4.3. Третий закон Ньютона(з-н парного взаимодействия м.т.)
 Силы, с которыми действуют друг на друга материальные точки,
Силы, с которыми действуют друг на друга материальные точки,
всегда равны по величине и направлены противоположно
вдоль прямой, соединяющей эти точки.

где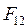 – сила, действующая на первую м.т. со стороны второй,
– сила, действующая на первую м.т. со стороны второй,
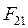 – сила, действующая на вторую м.т. со стороны первой.
– сила, действующая на вторую м.т. со стороны первой.
Эти силы приложены к разным материальным точкам (телам), всегда действуют парами и являются силами одной природы.
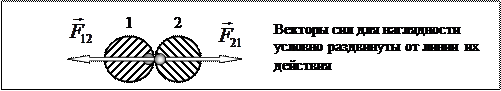 |
В общем случае 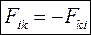
где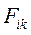 – сила, действующая на i-ю м.т. со стороны k-й,
– сила, действующая на i-ю м.т. со стороны k-й,
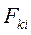 – сила, действующая на k-ю м.т. со стороны i-й.
– сила, действующая на k-ю м.т. со стороны i-й.
Третий закон Ньютона является дополнением к первым двум. Он позволяет осуществить переход от динамики отдельной материальной точки к динамике системы материальных точек. Это следует из того, что и для системы м.т. взаимодействие сводится к силам парного взаимодействия между материальными точками.
Из третьего закона Ньютона следует, что в любой замкнутой механической системе геометрическая сумма всех внутренних сил равна нулю:
 ,
,
где n – число материальных точек, входящих в состав системы.
Главным вектором внешних сил Fвнешн называется вектор, равный геометрической сумме всех внешних сил:
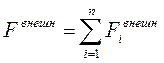 ,
,
где 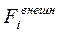 - результирующая внешних сил,
- результирующая внешних сил,
приложенных к i-й мат. точке.
Из второго и третьего законов Ньютона следует, что первая производная по времени t от импульса p механической системы равна главному вектору всех внешних сил, приложенных к системе:
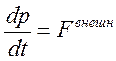 .
.
Дата добавления: 2014-12-20; просмотров: 1305;
