Предмет и метод дисциплины. Задачи курса
Конспект лекций по начертательной геометрии
Для аудиторной и самостоятельной работы
Студентов технических специальностей
Сарапул
Составитель Русинова Людмила Петровна, к.п.н., доцент кафедры ТММСиИ
Конспект лекций по начертательной геометрии для аудиторной и самостоятельной работы предназначен для студентов инженерно-технических специальностей.
В лекциях изложен основной материал по всем темам дисциплины. Материал подкрепляется иллюстрациями в цветном изображении. В начале каждой лекции дается план занятий и ссылки на учебную литературу, используемую как дополнительный источник информации.
Конспект лекций по начертательной геометрии для аудиторной и самостоятельной работы рассмотрен и одобрен на заседании кафедры технологии машиностроения, металлорежущих станков и инструментов
19.01. 2010 г.протокол № 1
дата
Тема 1. Проекции и их свойства
1. Предмет и метод дисциплины. Задачи курса.
2. Центральная проекция и её свойства.
3. Параллельная проекция и её свойства.
4. Аксонометрическая проекция.
5. Развитие геометрии: Эвклид => Лобачевский => Риман.
Литература: введение, § 1, 2, 71…75 [1]
Предмет и метод дисциплины. Задачи курса
Учебная дисциплина «Начертательная геометрии и инженерная графика» даёт студентам знания, которые необходимы им для общения с техническими специалистами на специальном графическом языке. Дисциплина включает следующие разделы: начертательную геометрию, машиностроительное черчение (инженерную графику) и основы компьютерной графики.
В первом семестре изучается начертательная геометрия, представляющая собой раздел геометрии, в котором пространственные формы предметов действительного мира и соответствующие геометрические закономерности изучаются при помощи изображений на плоскости – чертежей. Чертеж при этом является инструментом, с помощью которого осуществляется непосредственное изучение геометрических форм предметов и выполняется решение пространственных задач. Не всякое изображение предмета на листе бумаги позволяет точно определить его геометрическую фигуру. Для того, чтобы чертеж был геометрически равноценным изображаемому предмету (а только в этом случае можно изучать сам предмет по его чертежу), он должен быть построен при помощи метода проецирования (от латинского слова ргоjесеге – бросать вперед). Поэтому чертежи, применяемые в начертательной геометрии и инженерной графике, носят название проекционных чертежей.
Среди требований, предъявляемых к чертежам, наиболее существенными являются:
Ø наглядность – давать пространственное представление изображённого предмета;
Ø обратимость – по чертежу можно однозначно воспроизвести форму и размеры изображённого предмета.
Перед начертательной геометрией стоят следующие основные задачи:
1) разработка способов построения чертежей пространственных предметов на плоскости;
2) изучение способов решения и исследования пространственных задач при помощи чертежей;
3) развитие пространственного воображения.
В настоящее время чертежи используются практически во всех областях науки и техники. Ни одна, даже самая простая деталь не изготавливается без чертежа. «Чертеж является языком техники», – говорил один из создателей начертательной геометрии французский ученый и инженер Гаспар Монж (1746-1818). Причем этот язык является интернациональным, он понятен любому технически грамотному специалисту, независимо от того, на каком языке он говорит. Дополняя высказывание Монжа, профессор В.И.Курдюмов (1853-1904) – автор классического русского учебника начертательной геометрии – писал: «Если чертеж является языком техники, то начертательная геометрия служит грамматикой этого языка, так как она учит нас правильно читать чужие и излагать наши собственные мысли, пользуясь в качестве слов одними только линиями и точками, как элементами всякого изображения».
Нужно отметить, что начертательная геометрия и инженерная графика входит в число фундаментальных дисциплин, составляющих основу инженерного образования. Без знания начертательной геометрии и инженерной графики невозможно усвоение технических и специальных дисциплин на следующих курсах обучения.
2. Центральная проекция и её свойства
Как уже было отмечено выше, методом начертательной геометрии является метод проекций. Сущность этого метода рассмотрим на примере центральной проекции. Пусть дана некоторая плоскость П', которую назовем плоскостью проекций, и вне её точка S, называемая центром проекций. Для построения проекции некоторой точки А проводят через неё и центр проекций S прямую SА, называемую проецирующей прямой, а затем находят точку пересечения этой прямой с плоскостью П' – точку А'. Эта точка и называется центральной проекцией точки А на плоскость П' (рис.1.1). Таков метод центрального проецирования точек. Проецирование можно выполнить для любой точки пространства, за исключением точек, лежащих в плоскости, проходящей через центр проекций S и параллельной плоскости проекций П'. За проекции таких точек принято считать бесконечно удаленные точки плоскости П', которые называются несобственными точками плоскости (рис.1.2). И только для центра проекций S проекцию построить нельзя, т.к. проецирующая прямая при этом становится неопределенной.
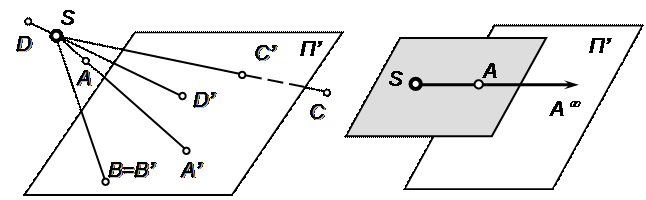
Рис.1.1. Центральная проекция Рис.1.2
Если задана какая-либо геометрическая фигура, то проекцией этой фигуры будет являться совокупность проекций всех её точек (рис.1.3).
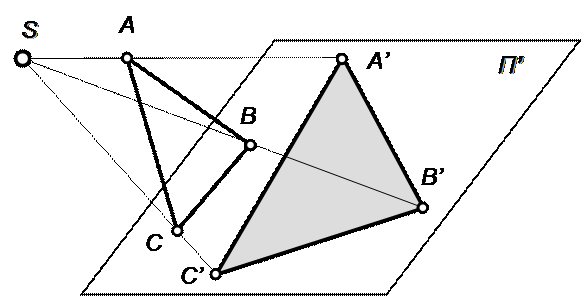
Рис.1.3
Свойства центральной проекции:
1) проекцией точки является точка;
2) проекцией прямой линии является прямая линия;
3) проекцией точки, лежащей на некоторой прямой, является точка, лежащая на проекции данной прямой.
Метод центрального проецирования слишком сложен и в значительной степени искажает форму и размеры оригинала, т.к. не сохраняет параллельности прямых и отношения отрезков. Поэтому в технике этот метод не применяется, а используется лишь художниками при написании картин – метод перспективы (глаз человека устроен по типу центральной проекции).
Дата добавления: 2014-12-18; просмотров: 1147;
