Параллельная проекция и ее свойства

Параллельная проекция является частным случаем центральной, когда центр проекций S удален в бесконечность. При этом задается направление проецирования, параллельно которому проводятся проецирующие лучи. Пусть дана плоскость проекций П' и точка А (рис.1.4). Для построения проекции точки проведем через точку А проецирующую прямую параллельно заданному направлению проецирования S. Затем определим точку пересечения этой прямой с плоскостью П' – точку А′, которая называется параллельной проекцией точки А.

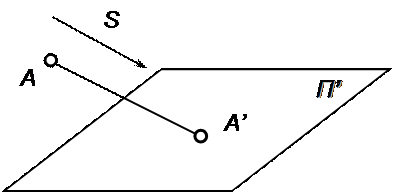
Рис.1.4. Параллельная проекция

Параллельная проекция кроме трех свойств центральной проекции обладает еще дополнительными свойствами:

4) проекциями параллельных прямых являются параллельные прямые;

5) отношение проекций отрезков, лежащих на параллельных прямых или на одной и той же прямой, равно отношению самих отрезков;

6) проекция фигуры не меняется при параллельном переносе плоскости проекций.

Эти свойства параллельной проекции обеспечивают более простое построение чертежа, меньше искажающего форму и размеры оригинала по сравнению с центральной проекцией. Так в связи с сохранением параллельности прямых параллельной проекцией параллелограмма является параллелограмм, а трапеции – тоже трапеция, в то время как в центральной проекции эти фигуры проецируются в четырехугольники произвольного вида.

В зависимости от величины угла, образованного направлением проецирования S с плоскостью проекций П', параллельная проекция подразделяется на ортогональную (прямоугольную), когда угол равен 90°, и косоугольную в остальных случаях.

В ортогональной проекции нетрудно установить соотношение между длиной натурального отрезка и длиной его проекции. Если отрезок АВ образует с плоскостью проекций угол a, то, проведя АВ*||А'В' (рис.1.5), получим из прямоугольного треугольника АВ*В: АВ*=АВсоs(a) или А'В'=АВсоs(a).

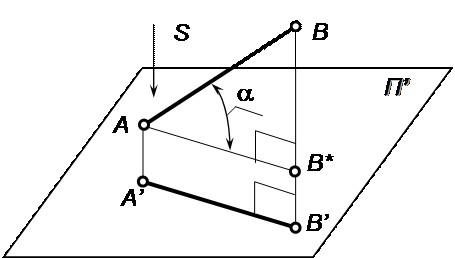
Рис.1.5

Ортогональная проекция получила наибольшее распространение в технических чертежах, т.к. она позволяет наиболее легко судить о размерах изображаемых предметов.

Рассмотренные выше методы проецирования однозначно решают прямую задачу – по данному оригиналу построить его проекционный чертеж. Однако обратная задача – по данному проекционному чертежу воспроизвести (реконструировать) оригинал – не решается однозначно. Эта задача допускает бесчисленное множество решений, т.к. точку А', например, можно считать проекцией любой точки проецирующей прямой, проходящей через А (рис.1.1, 1.4). Таким образом, рассмотренные проекционные чертежи не обладают свойством обратимости. Для получения обратимых чертежей нужно дополнить проекционный чертеж некоторыми данными. Существуют различные методы такого дополнения. В данном курсе мы будем рассматривать два вида обратимых чертежей, а именно, аксонометрические и комплексные чертежи в ортогональных проекциях.