Экономико-математические, факторные и структурные модели в прогнозировании.

Экономико-математическая модель это система формализованных соотношений, описывающих основные взаимосвязи элементов, образующих экономическую систему. Система экономико-математических моделей эконометрического типа служит для описания относительно сложных процессов экономического или социального характера.

Простейшая экономика-математическая модель может быть представлена, например, в следующем виде [19]:

Z = a * х(17)

Такая модель может быть использована, например, для определения потребности в материалах, требующихся для изготовления какого-либо изделия. В этом случае Z – общая потребность в материалах, "а" – норма расхода материала на одно изделие, "х"- количество изделий.

Эта модель приобретает более сложный вид, если определяется потребность в материалах для изготовления нескольких видов изделий [19]:

Z = а1х1 + а2х2 + … + аnхn

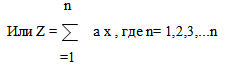(18)

Эта модель показывает зависимость потребности в материалах от двух факторов: количества изделий и норм расхода материалов и называется дескриптивной (описательной).

Определенные виды моделей экономического и социального прогнозирования могут классифицироваться в зависимости от критерия оптимизации или наилучшего ожидаемого результата. Так, например, различают экономико-математические модели, в которых минимизируются затраты, и модели в которых желательно получить, например, максимум продукции.

С учетом фактора времени модели могут быть статическими, когда ограничения в модели установлены для определенного отрезка времени, или динамическими – в этом случае ограничения установлены для нескольких отрезков времени.

Различают факторные и структурные модели экономического типа. Один и тот же тип моделей может быть применим к различным экономическим объектам. В зависимости от уровня рассмотрения показателей народного хозяйства различают макроэкономические, межотраслевые, отраслевые и региональные модели.

Факторные модели описывают зависимость уровня и динамики того или иного показателя от уровня и динамики влияющих на него экономических показателей – аргументов или факторов. Факторные модели могут включать различное количество переменных величин и соответствующих им параметров. Простейшими видами факторных моделей являются однофакторные, в которых фактором является какой-либо временный параметр. Многофакторные модели позволяют одновременно учитывать воздействие нескольких факторов на уровень и динамику прогнозируемого показателя.

В практике экономического прогнозирования для оценки роли отдельных факторов выпуска продукции используется математическая формула, показывающая зависимость объема созданной продукции от функционирования основных факторов производства, их количественного и качественного состава. Она получила название производственной функции. Производственная функция на микроуровне выражает техническое соотношение между количеством факторов, используемых производителями, и объемом полученной продукции. В самом общем виде эта зависимость может быть представлена следующим образом [19]:

У = f (а1, а2,…аn),(19)

где У – объем продукции,

а1, а2…аn – использованные факторы производства.

При этом различают факторы внутренние (эндогенные) и внешние (экзогенные).

Для более углубленного анализа динамики экономического роста на макроуровне была изучена взаимосвязь между объемом производства и его различными факторами. Первым вариантом явилась производственная функция Кобба – Дугласа, показывающая зависимость общего выпуска продукции от двух факторов: капитала и труда. В дальнейшем было учтено также влияние третьего фактора – технического прогресса. В итоге модель Кобба – Дугласа приняла следующий вид:

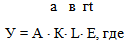
У – объем выпуска продукции, А – коэффициент сопряжения размерности элементов формулы, К – затраты капитала, "а" – коэффициент, характеризующий прирост объема выпуска продукции, приходящейся на 1% прирост капитала, L – затраты труда, в – коэффициент, храктеризующий прирост объем выпуска продукции, приходящийся на 1% прироста затрат труда, "е" – фактор, отражающий влияние технического прогресса (r) и времени (t).

Структурные модели описывают соотношения, связи между отдельными элементами, образующими одно целое или агрегат. Эти модели являются моделями структурно-балансового типа, где наряду с разбивкой какого-либо агрегата на составляющие элементы рассматриваются взаимосвязи этих элементов. Такие модели имеют матричную форму и применяются для анализа и прогноза межотраслевых и межрайонных связей. С их помощью описывается взаимосвязи потоков, например, межсекторные поставки продукции. Наиболее распространенной формой структурно-балансовой модели является межотраслевой баланс производства и распределения продукции.

Комплекс межотраслевых моделей включает укрупненную динамическую и развернутую натурально-стоимостную модели. Единство системы обеспечивается использованием для построения натурально-стоимостного межотраслевого баланса основных показателей укрупненной динамической модели таких как ВВП, структура его распределения, а также показателей, характеризующих потребность отраслей материального производства в продукции других отраслей, в инвестициях и т.д.

В зависимости от номенклатуры продукции, используемого сырья и др. различают однопродуктовые и многопродуктовые модели. К первым относятся модели, в которых установлено одно ограничение по спросу на продукцию, вырабатываемую отраслью в целом, либо одно ограничение на количество сырья или другого ресурса, потребляемого ею. Например, в топливной промышленности может быть установлено одно такое ограничение – по теплотворной способности энергоносителя.

В многопродуктовых моделях рассматриваются два и более ограничений по спросу на продукцию, вырабатываемую отраслью в целом, и на потребление сырья или любого другого ресурса.