Дискретизация и континуализация

Дискретизация. Если исходное описание линейной системы непрерывно, часто можно перейти к дискретному описанию при помощи следующей процедуры.

Пусть состояние x(t) системы (11) доступно измерению в дискретные моменты времени t_k=kh, k=0, 1……., где k>0 – шаг дискретности. Пусть u(t) постоянно на промежутках между моментами коррекции t_k. Тогда динамику векторов x_k=x(tk) можно описать разностными уравнениями (13), в которых матрицы P и Q определяются соотношениями

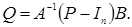(19)

Здесь e^Ah – экспоненциал матрицы А, определяется формулой

(20)

Если предположение о кусочном постоянстве u(t) не выполняется, то переход от (11) к (13) является приближенным, но его точность растет по мере уменьшения шага h. При достаточно малых h для вычисления e^Ah можно удерживать лишь несколько членов ряда (11) или аппроксимировать сумму (11) каким-либо способом.

Например, при переходе от (11) к (13) можно пользоваться формулой 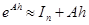, соответствующей численному интегрированию (11) методом Эйлера. При такой аппроксимации передаточные функции дискретной и непрерывной систем будут связаны соотношением

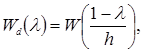(21)

т.е при переходе к дискретному времени в передаточной функции W(p) системы (16) нужно заменить p на (1-z)/h. Если матрица A гурвицева, т.е. Re λ_i(A)<0, то метод Эйлера дает устойчивую аппроксимацию лишь при

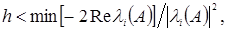(22)

где λ_i(A) - собственные числа матрицы А (корни полинома А(λ)). Целый ряд способов перехода от (11) к (13) основан на аппроксимации матрицы e^Ah дробями Падэ. Частными случаями этих способов является метод Тастина (формула Падэ порядка)

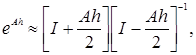(23)

приводящий к соотношению между передаточными функциями

(24)

а также метод Дэвисона (формула Падэ порядка)

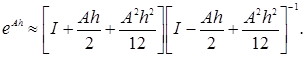(25)

Отметим, что (23) и (25) дают устойчивые аппроксимации при любом h>0 (разумеется, если А гурвицева).

Если непрерывная система нелинейна, то для перехода к ее дискретному описанию также можно использовать методы численного интегрирования. Например, метод Эйлера дает для системы (9) дискретное описание:

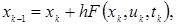
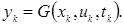(26)

Континуализация – это переход от дискретной математической модели системы к непрерывной. Если дискретная модель системы имеет вид (13), то перейти к непрерывной модели (11) можно по формулам

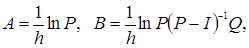(27)

Вытекающими из (11), где lnP – логарифм матрицы – функция, обратная к экспоненциальной и также определяемая через ряд

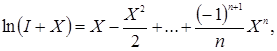(28)

сходящийся при ||Х|| < l (Х=Р-I). С точностью до величин порядка h² можно ограничиться формулами

(29)

соответствующими методу Эйлера. Однако удобнее всего переходить от дискретной передаточной функции к непрерывной по формулам (23) и (26). Например, по методу Эйлера (21) достаточно заменить в передаточной функции 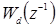переменную 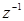на 1 - hp.

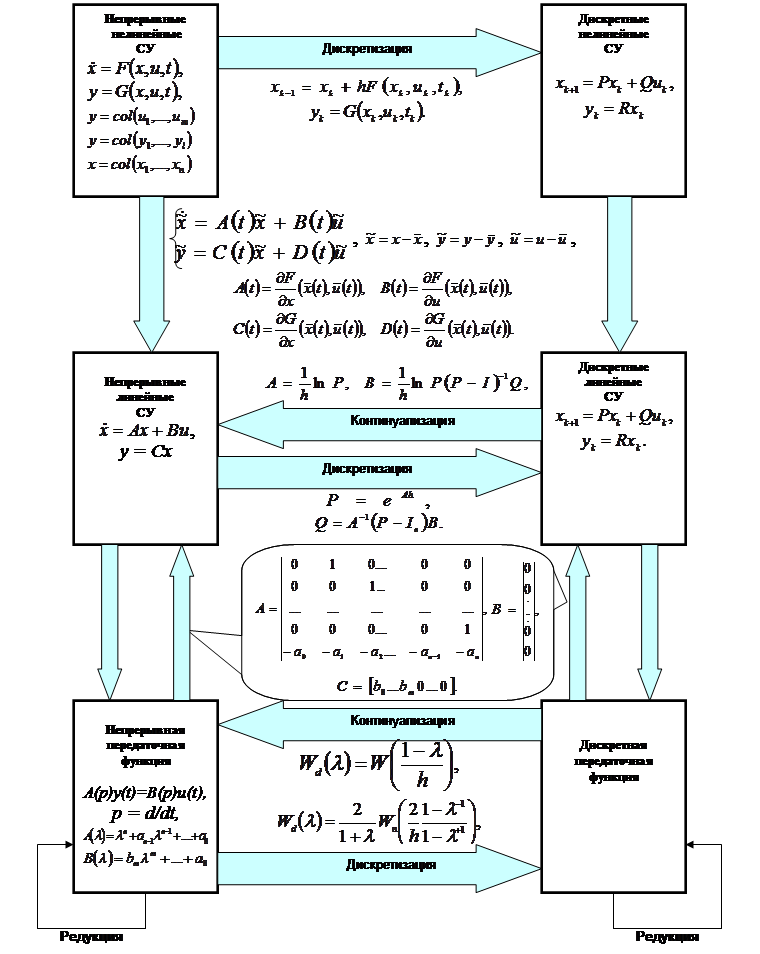
При исследовании линейных систем получили распространение также методы упрощения описаний систем путем редукции - (понижения порядка). Взаимосвязь различных описаний динамических систем представлена на рис. 1.