Дискретизация модели. Сеточная модель пласта.

Уравнения, описывающие математическую модель фильтрации в большинстве случаев невозможно решить аналитическими методами. Поэтому применяются численные методы решения уравнений фильтрации – конечно-разностная аппроксимация. В силу нелинейных зависимостей свойств пласта и флюидов от давления, насыщенностей, температур, концентрации, конечно-разностные уравнения носят нелинейный характер. Конечно-разностные методы решения уравнений фильтраций, в том числе методы линеаризации, подробно описаны в работах. Процесс получения конечно-разностных уравнений, называется дискретизацией; причём дискредитируется как пространство, так и время. При дискретизации используют метод сеток, типичная сеточная модель:

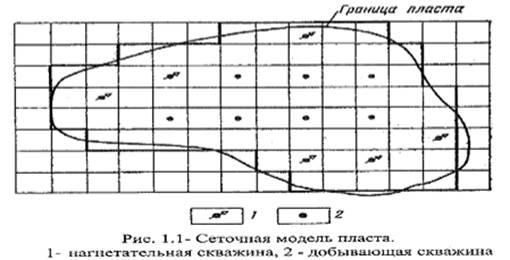
Пласт разделятся на блоки – ячейки и составляется баланс массы и энергии для всех блоков одновременно. Использование большого числа ячеек позволяет учесть свойства породы и флюидов, которые могут изменяться от ячейки к ячейке.

Численные модели были разработаны в середине 50-х годов Писманом и Рэкфордом. Таким образом, задача решения дифференциальных уравнений сводится к задаче решения алгебраических уравнений.

Современные гидродинамические симуляторы программных комплексов используют несколько сеток:

1) равномерная прямоугольная сетка (глубина и толщина каждого слоя одинаковые) – X, Y Regular. Задаётся число ячеек по осям координат X,Y,Z и размеры ячеек по координатам X,Y,Z (обычно размер ячеек по X,Y от 25 до 100 , по Z от десятых долей метра до нескольких метров). Совокупность ячеек представляет собой трехмерную сетку (3D);

2) неравномерная прямоугольная сетка (различная глубина и толщина каждого слоя). Задают число ячеек по координатам в виде текстового файла;

3) неравномерная сетка с геометрией Corner Point (угловой точки), обычно используется в секторных моделях. Задаётся число ячеек по осям координат X,Y,Z и координаты узлов в виде текстового файла. Данная сетка является более гибкой т.к. вследствие варьирования размерами ячеек можно учитывать послойную неоднородность продуктивного пласта с числом слоёв от десятков до сотен;

4) радиальная сетка. Указывается число слоёв, сектором в радиальном и угловом направлениях, размеры секторов.