Псевдофизические логики

Пополнение знаний

Пополнение БЗ осуществляется различными методами

· при об­щении с внешней средой,

· при постановке новых задач,

· при дос­тижении новых целей.

Кроме того, пополнение знаний осуществ­ляется самой ИнС на основе имеющейся БЗ и машин (программ) логического вывода новых знаний. Это ведет к устранению трудно­сти, связанной с ограниченностью знаний.

Проблема пополнения знаний возникла при решении задач:

· понимания естественного языка,

· обучения,

· поиска ответов на во­просы к БЗ,

· анализа ситуаций, сцен и др.

Знания могут быть пред­ставлены в виде фактов, хранящихся в БЗ, или в виде описания си­туаций, поступающих на вход ИнС.
Укажем несколько подходов к пополнению знаний:

· модели «здравого смысла»;

· сценарии;

· подход, опирающийся на идею о том, что физические закономерности внешнего мира могут быть описаны в рамках специальных псевдофизических логик (рис. 3.1).

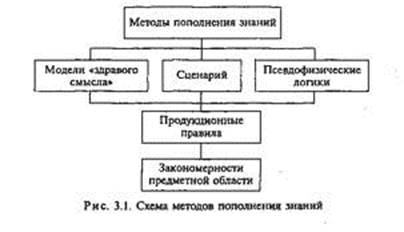
Все подходы в той или иной степени используют идею продукци­онных правил. Система продукций отражает закономерности, при­сущие заданной проблемной области. Например, для ситуаций, описывающих статистические пространственные отношения между объектами, можно выбрать следующие продукции: х Содержится в> у, У Содержится в> z —> х Содержится в> z (свойство вложен­ности, которое выполняется в «матрешках»); х<находится на> у, г<находится на> x-»z <находится на> у.

Пополняя постепенно БЗ продукциями такого типа, можно в ИС создать достаточно мощные средства для порождения новых фактов из тех, которые в ней имеются. Процедуры пополнения знаний отличаются друг от друга структурой продукционных пра­вил и стратегий управления в системе продукций.

Псевдофизические логики

Здесь физическая модель предметной области переносится на язык логики (язык ЭВМ). При определен­ных стратегиях управления система продукций превращается в дедуктивную логическую систему. Широкий класс таких систем на­зывается псевдофизическими логиками (ПФЛ). В их аксиомах и пра­вилах вывода используются не только реальные физические свойства окружающего мира, но и особенности его восприятия челове­ком.

Виды:

· временных логик,

· статической пространст­венной логики,

· фрагменты логики действий

· каузальной логики (рис. 3.2).

ПФЛ обладает рядом особенностей:

2. Часть рассуждений в ПФЛ связана со шкалами:

· метрически­ми

i. абсолютными (задан некоторый масштаб и выбрана точка отсчета)

ii. относительными (указывается лишь расстояние меж­ду точками, а начало отсчета может «плавать»)

· топологическими (топологическая шкала представляет собой порядковую шкалу. На ней указываются отношения порядка (строгого, нестрогого, размытого) между упо­рядочиваемыми)

3. ПФЛ содержат в качестве аксиом-утверждения, вытекающие из восприятия мира человеком, которые подтверждаются результа­тами соответствующих психологических экспериментов.

4. Совокупность ПФЛ характеризуется связями между отдель­ными частями — логиками (например, логика времени тесно связа­на с логиками пространства и действий).

Каждая ПФЛ является системой, включающей модель предмет­ной области в виде понятий и отношений, существующих в ней, и модель вывода. Первая модель задает формальный язык описания знаний (ситуаций), вторая позволяет получать пополнение этих знаний (рис. 3.3.).

Пополнение знаний на основе сценариев

Пополнение знаний можно выполнить с помощью сценариев. Перечислим основные схемы рассуждений на сценариях, используемых при выводе. Часть схем является интерпретацией значений слотов сценария (СЦ).

Из описания проблемной области выбирается сценарий, зна­чение слота «цель» которого соответствует поставленной цели.

Анализируются значения всех слотов указанного сценария и строится последовательность П|, являющаяся значением слотов «посылки» и «ключ» с их спецификациями. Выполняется последовательное обращение к сценариям, ука­занным в Щ

Взаимодействие базы знаний с внешней средой

При пополнении БЗ необходимо общение с внешней средой, как одним из источни­ков знаний. Сама по себе БЗ — это набор выявленных закономер­ностей, представленных с помощью одной из рассмотренных ранее моделей знаний.

К внешней по отношению к ней среде относятся источники знаний Z, фактов X и управляющих воздействии Ub U2, и3, а также рецепторы выводимого знания Y. Графически отноше­ния между этими переменными представлены на рис. 3.4.

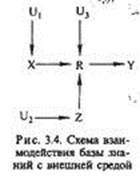
Аналитически эти отношения записываются следующим обра­зом.

U1 – управление на базу знаний

U2 – управление на источник знаний

U3 – управление на источник знаний

Относительно приведенных переменных и зависимостей базы знаний можно классифицировать следующим образом:

· с фиксированным и изменяемым множеством фактов X;

· с фиксированным и пополняемым знанием Z;

· с фиксированной и реструктурируемой закономерностью R.

В частном случае фиксированное множество фактов X может быть пустым: X = 0, При этом БЗ выполняет роль генератора ва­риантов предметного знания, подобно генера­тору сигналов. Информационные системы, ядром которых является генератор вариантов предметного знания, а назначением — порож­дение справочных данных в узкой ПО, называ­ют интеллектуальными справочниками [58].

Модель вывода генератором вариантов зна­ния

Описывается формальной системой F = = <Т, Р, А, В>
Ее символы интерпретируются соответст­венно как множества базовых элементов, синтаксических правил, аксиом и правил вывода (семантических правил).
Т – множество базовых элементов, т.е. алфавит ПО (логический, сло­варный, предметный и т.д.). Принадлежность элемента х алфа­виту Т устанавливается за конечное число шагов с помощью процедуры П(Т).
Р - синтаксические правила, которые задают ограничения на построение синтаксически правильных совокупностей — цепочек символов (формул, слов и предложений языка). Синтаксическая правильность: цепочек должна устанавливаться за конечное число шагов с помо­щью процедуры П(Р).
А – аксиомы, которые представляют собой подмножество синтаксически правильных совокупностей (формул), общезначимых в ПО. Для проверки общезначимости должна существовать конечная про­цедура П(А). В качестве таковой используется построение таблиц истинности для соответствующей формулы.
В – множество правил вывода, которые порождают новые семантически правильные совокупности, к которым также применимы правила вывода. Таким образом, формируется множество выводимых в фор­мальной системе совокупностей.
Например:

Т - множество букв русского алфавита

Р – правила сочетания этих букв («шЫ»)

А – элементы множества – приставка, корень и т.д.

В – присоединение и подстановка – правила выводы.
Формальная система непротиворечива, если в ней не найдется такой формулы, что и она сама, и ее отрицание выводимы;