Основные показатели термодинамических процессов идеальных газов в закрытых термодинамических системах
Изобарный процесс
В изобарном ТП как уже отмечалось выше имеют место условия:
P = constиdP = 0.
Такой ТПможет протекать, например, в цилиндре поршневого двигателя, поршень которого перемещается без трения так, что Ргаза в цилиндре равняется постоянному Рокружающей среды ОС, действующей на поршень с внешней стороны. Соответственно для этого объём ОСдолжен быть бесконечно большим. Только в этом случае внедрение поршня цилиндра в окружающую среду не приведёт к увеличению Р в ней.
Из уравнения Клапейрона Pv = RT, учитывая, что Ри R являются постоянными величинами, получаем:
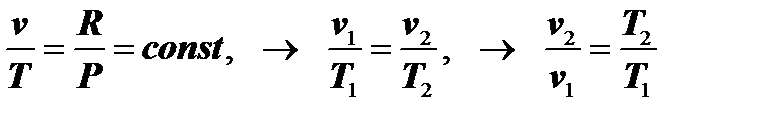 . (7.3.1)
. (7.3.1)
Полученные взаимосвязи параметров соответствуют условиям газового закона Гей-Люссака, график которого приведён на рисунке. Двигаясь по графику процесса от точки 1 к точке 2, видим, что v газа возрастает, а это в соответствии с (7.3.1) означает, что Т газа возрастает. Значит, процесс 1-2 протекает в режиме нагревания газа, а процесс 2-1 – в режиме охлаждения. График процесса является изобарой(изобара (греч.) – линия одинакового давления; изо– равный, одинаковый, барос– тяжесть, вес).
| Изображение изобарного процесса на Рv-диаграмме |
| P1 = P2 |
| v |
| P |
| q |
| q |
| v1 |
| v2 |
Таким образом, при изобарном ТП объём газавсегда пропорционален его абсолютной температуре Т. Соответственно, при расширении газа его Т в изобарном ТПвозрастает, а при сжатии – уменьшается.
При Р = const работа деформирования газав изобарном ТПбудет:
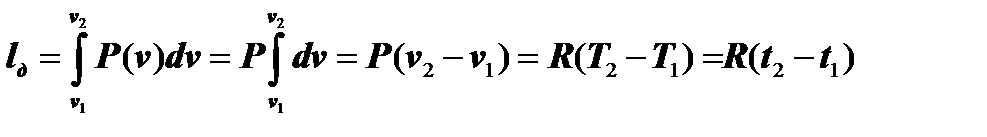 .(7.3.2)
.(7.3.2)
На графике процесса (см. рис.) работа деформирования газа lд соответствует площади S1-2-3-4-1. При прямом процессе 1-2, когда v2 > v1, тепло поступает в газ, он нагревается и, соответственно, lд > 0. При обратном процессе 2-1, когда v2 < v1, тепло уходит из газа, он охлаждается и в этом случае lд < 0.
Располагаемая работа в изобарном ТП равна:
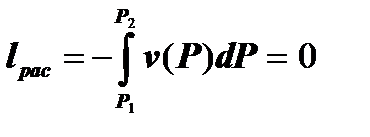 . (7.3.3)
. (7.3.3)
Равенство нулю располагаемой работы вызвано тем, что в изобарном ТПни сжатия газа, ни его разряжения не происходит. Как известно, процесс сжатия газа предопределяет повышение его P, а разряжение - уменьшение P. В изобарном ТП этого нет. В течение всего процесса Ргаза остаётся постоянной величиной, равной Р окружающей среды ОС. Отсутствие перепада давления между рабочим телом и ОС не позволяет реализовать хотя бы часть работы деформирования газа в техническую, то есть полезную, работу.
Количество тепла, участвующее в процессе определяется следующим образом:
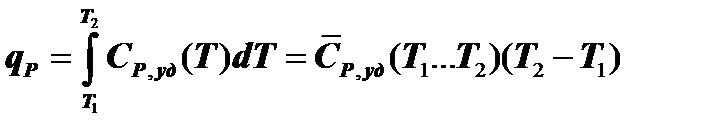 . (7.3.4)
. (7.3.4)
Выше (см. (5.4.9)) было показано, что в изобарном ТП
qР = Di(Т1…Т2) = i2 – i1,
то есть всё тепло, подводимое (отводимое) в этом процессе к рабочему телу, идёт на увеличение (уменьшение) его энтальпии. Следовательно, изменение энтальпии рабочим телом может быть определено по формуле (7.3.4).
Величину qР в принципе можно определить и другим способом, что позволит, например, оценить точность расчётов по формуле (7.3.4). Учитывая, что Р = Р1= Р2 , из уравнения Клапейрона имеем:
 .
.
Далее, учитывая уравнение Майера, получаем:
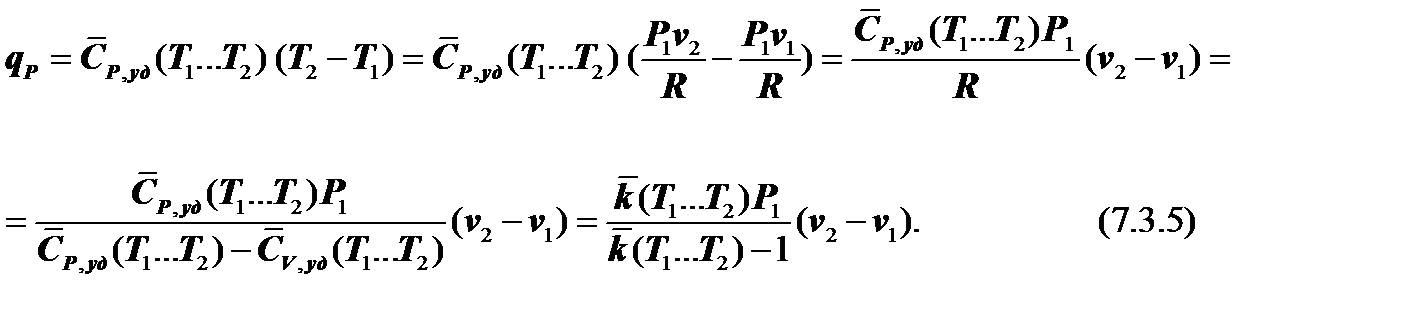

где 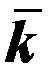 (Т1…Т2 ) – показатель адиабаты рабочего тела (газа), усреднённый в диапазоне температур от Т1 до Т2.
(Т1…Т2 ) – показатель адиабаты рабочего тела (газа), усреднённый в диапазоне температур от Т1 до Т2.
При изобарном ТП имеет место изменение температуры рабочего тела. Следовательно, изменяется и его внутренняя энергия и, что может быть определено, как показано выше, по формуле (5.3.10).
Для определения доли тепла, затрачиваемого в изобарном ТП на работу деформирования рабочего тела, разделим левую и правую части уравнения
1-го закона термодинамики (5.3.3) на dq:
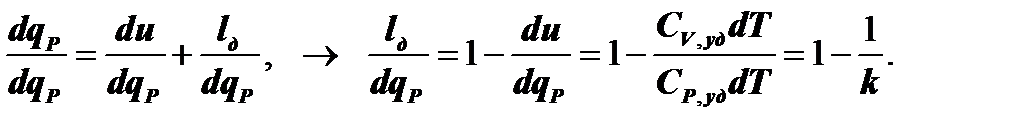 (7.3.6)
(7.3.6)
Следовательно:
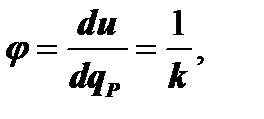 а
а 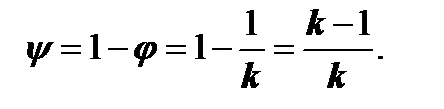 (7.3.7)
(7.3.7)
Если принять k » 1,40, что соответствует двухатомным газам, то
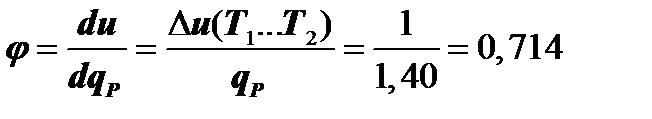 , а
, а 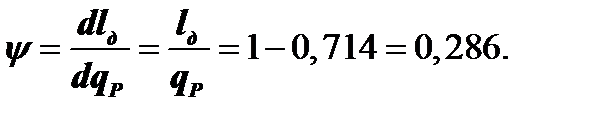
Следовательно, порядка 28,6 % всего подведённого (отведённого) к рабочему телу тепла в изобарном ТП двухатомного газа расходуется на совершение работы его деформирования, а 71,4 % - на изменение внутренней энергии.
Изменение энтропии в обратимом изобарном ТП можно определить из уравнения (6.4.6):
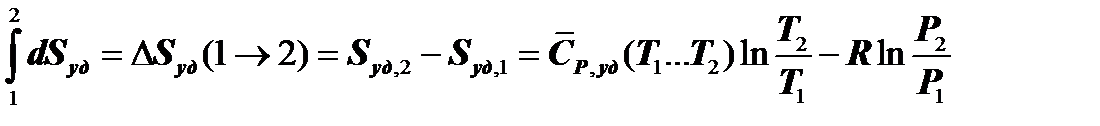
При Р = const ln(Р2 /Р1 ) =0, поэтому данное уравнение приобретает более простой вид:
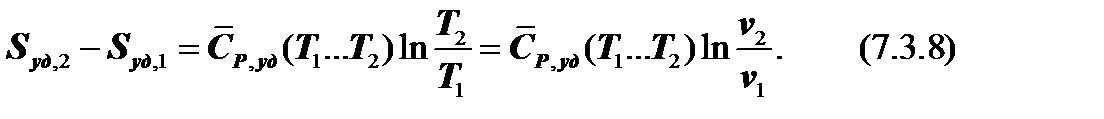
Полученное соотношение показывает, что изобарный ТП изображается на ТS–диаграмме логарифмической кривой.
Так как 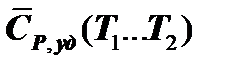 >
> 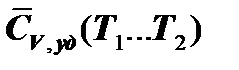 , то изменение энтропии при изобарном ТП будет больше, чем при изохорном и, кроме того, изобара на TS-диаграмме является более пологой кривой, чем изохора.
, то изменение энтропии при изобарном ТП будет больше, чем при изохорном и, кроме того, изобара на TS-диаграмме является более пологой кривой, чем изохора.
Соответственно, количество тепла на ТS–диаграмме изобарного ТП определяется площадью под изобарой 1-2, то есть S1-2-3-4-1.
| Т |
| Sуд |
| Т1 |
| Т2 |
| Sуд,1 |
| Sуд,2 |
| Изображение изобарного процесса на ТS-диаграмме |
Изохорный процесс
Изохорный ТП (V = const и v = const) может совершаться рабочим телом (газом), находящимся, например, в цилиндре поршневого двигателя при неподвижном поршне как в при нагреве рабочего тела, так и при его охлаждении.
Из уравнения Клапейрона Pv = RT, учитывая, что vи R являются постоянными величинами, получаем:
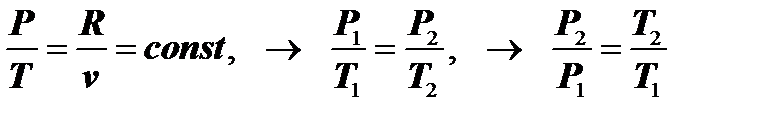 . (7.2.1)
. (7.2.1)
Полученные взаимосвязи параметров соответствуют условиям газового закона Шарля. Двигаясь по графику процесса от точки 1 к точке 2, видим, что Р газа возрастает, а это в соответствии с (7.2.1) означает, что Тгаза возрастает. Значит, процесс 1-2 протекает в режиме нагревания газа, а процесс 2-1 – в режиме охлаждения. График процесса является изохорой (изохора (греч.) – линия одинакового объёма; изо – равный, одинаковый, хора – место, пространство).
| P1 |
| v |
| P |
| v = v1 = v2 |
| q |
| q |
| P2 |
Изображение изохорного процесса на Pv-диаграмме
Равенство v = const предопределяет dv = 0. Поэтому работа деформирования рабочего телав данном ТПбудет равна нулю и изохора на графике процесса проектируется в точку:
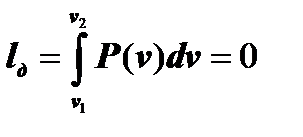 , (7.2.2)
, (7.2.2)
а располагаемая работа:
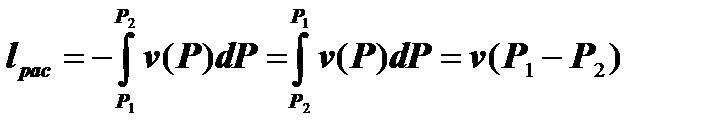 . (7.2.3)
. (7.2.3)
На графике процесса lрас соответствует площади S1-2-3-4-1.
Таким образом, несмотря на то, что работа деформирования рабочего теларавна нулю, нагрев этого тела, способствующий повышению его давления с Р1 до Р2 , увеличивает, относительно начальных параметров состояния, запас энергии в рабочем теле. Эта энергия представляет собой потенциальную энергию деформирования рабочего тела, которая автоматически преобразуется в техническую работу при создании определённых условий, например, если поршень получит возможность продольного перемещения. Поэтому иногда располагаемую работу называют потенциальной работой, причём не только для изохорного ТП. При охлаждении же рабочего телазапас потенциальной энергии его деформирования, относительно начальных параметров состояния, уменьшается. Располагаемая работа в этом случае становится отрицательной.
Количество тепла, участвующего в процессе, определяется следующим образом:
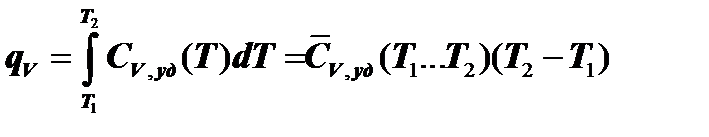 . (7.2.4)
. (7.2.4)
Величину qV в принципе можно определить и другим способом, что позволит, например, оценить точность расчётов по формуле (7.2.4). Учитывая, что v =v1= v2, из уравнения Клапейрона имеем:
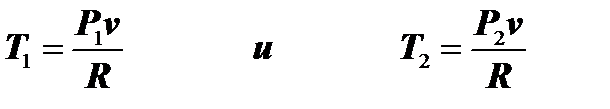 .
.
Далее, учитывая уравнение Майера, получаем:
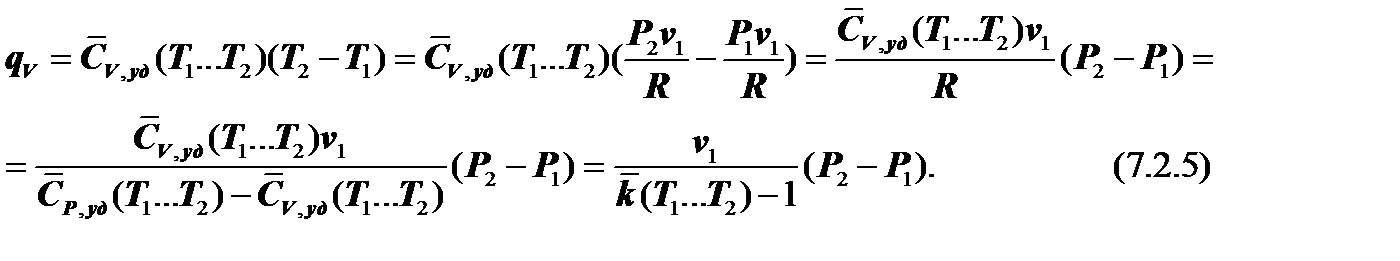

Учитывая 1-й закон термодинамики для изохорного ТП, определим изменение внутренней энергии рабочего тела:
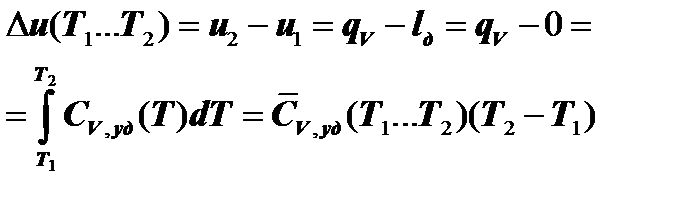 .(7.2.6)
.(7.2.6)
Следовательно, при изохорном ТПвсё тепло расходуется только на изменение внутренней энергии рабочего тела.
Если изохорный ТП осуществляется с увеличением Р, тепло в нём подводится к рабочему телу, при этом увеличиваются его u и Т. Если же Рпонижается, то u и Т рабочего тела уменьшаются.
Изменение энтальпии рабочего тела в изохорном ТП будет равно:

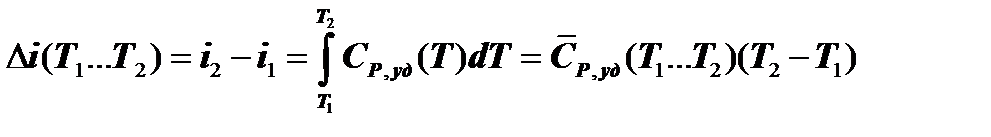 .(7.2.7)
.(7.2.7)
Величину Di можно также определить способом, использованным выше для расчёта qV.
Изменение энтропии в обратимом изохорном ТПможно определить из уравнения (6.4.3). При v = const ln(v2 /v1 ) = 0, поэтому данное уравнение приобретает более простой вид:
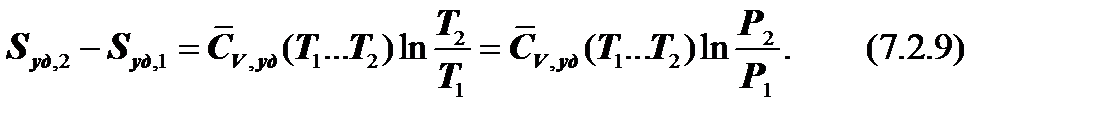
Полученное соотношение показывает, что изохорный ТП изображается
| Т |
| Sуд |
| Т1 |
| Т2 |
| Sуд,1 |
| Sуд,2 |
Дата добавления: 2017-03-29; просмотров: 656;
