Скорость распространения гидравлической ударной волны в трубопроводе
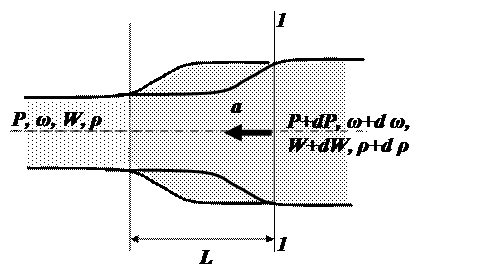Изменения давления и скорости потока в трубопроводах происходят не мгновенно в связи с упругостью твёрдых стенок трубы и сжимаемостью рабочей среды, а с некоторой конечной скоростью, обусловленной необходимостью компенсации упругих деформаций жидкости и трубы. Рассмотрим случай когда в трубопроводе длиной L и площадью сечения ωпод давлением Р находится жидкость, плотность которойρ.Предположим, что в момент времени t в сечении 1 – 1 давление повысится на величину dp. Это повышение вызывает увеличение плотности на величину dρ, а также расширение внутреннего диаметра трубы. Следовательно, площадь проходного сечения увеличится на величину dω. В результате увеличится объём W участка трубы на величину dW. За счёт этого произойдет увеличение массы жидкости находящейся в трубе на участке длиной L. Масса увеличится за счёт увеличения, во-первых, плотности жидкости, во-вторых, за счёт увеличения объёма W.
Такая ситуация рассматривалась при выводе уравнения неразрывности потока в дифференциальной форме, с той только разницей, что там рассматривалось лишь изменение массы во времени, без учёта вызвавших это изменение причин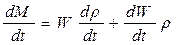 
. По аналогии с приведённым уравнением запишем выражение, описывающее изменение массы за счёт изменения давления
.
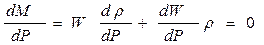Жидкость под действием указанного повышения давления устремится с некоторой скоростью а в слои с меньшим давлением, в которых также будет повышаться плотность и увеличиваться напряжение в стенках трубопровода, способствующее увеличению площади трубопровода. В связи с этим потребуется некоторое время на распространение этих деформаций вдоль трубопровода.
С другой стороны, перемещение массы dm за время dt происходит под влиянием результирующей Fр сил давления, действующих вдоль линии движения на торцовые поверхности цилиндрического объёма длиной L
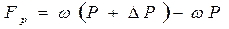
В этом случае уравнение импульса силы может быть представлено в следующем виде
.
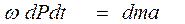Отсюда
.
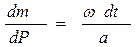Имея в виду, что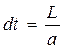 
, и подставив это в предыдущее выражение, получим
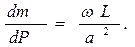
Заметим, что произведение
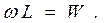
Приравняем оба выражения для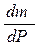 
и получим:
.
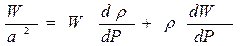Выразим из последнего равенства величину a2
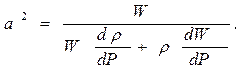
Разделим числитель и знаменатель на W, а первое слагаемое в знаменателе искусственно умножим и разделим на ρ:
.
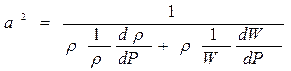Обратим внимание на то, что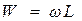 
а 
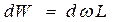. После подстановки этих равенств в последнее выражение и извлечения корня получим выражение для скорости распространения ударной волны, которая, по сути, является скоростью распространения упругих деформаций жидкости в трубе.
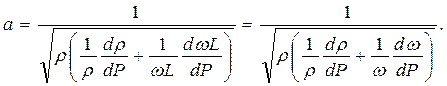
Здесь первое слагаемое под корнем характеризует упругие свойства рабочей среды (жидкости), а – второе упругие силы материала трубы.
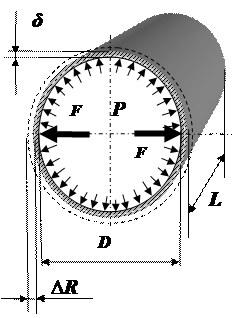Рассмотрим подробнее эти слагаемые.
Как известно из гидростатики, сила, действующая на цилиндрическую поверхность, равна произведению давления на проекцию площади этой поверхности в направлении действия силы. На рассматриваемый участок трубы с толщиной стенок δ, длиной L и диаметром D действует изнутри давление P. Вследствие этого возникает разрывающая сила F, равная
.
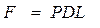В стенках трубы возникает сила сопротивления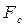 
, равная произведению площади сечения стенок трубы 
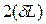на внутренние напряжения 
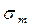в материале стенок трубы, т.е.
.
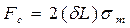Если приравнять две эти силы, получим равенство
,
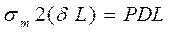из которого найдём выражение, определяющее внутреннее напряжение в стенках трубы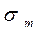 
:
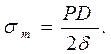
Полагая, что относительное увеличение диаметра трубы, равное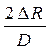 
, прямо пропорционально напряжению в стенках трубы, можно записать
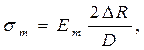
где Ет - коэффициент пропорциональности, который является модулем упругости материала трубы.
Из двух последних выражений следует, что абсолютное приращение радиуса сечения трубы может быть выражено формулой
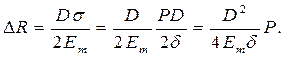
Запишем выражение, определяющее увеличение площади сечения трубы:
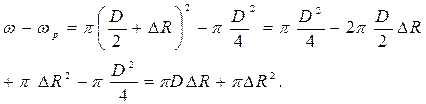
где ω – начальная площадь сечения трубы,
ωр – площадь сечения трубы при давлении P.
Пренебрегая малой величиной высшего порядка ΔR2 и подставив выражение для ΔR, получим
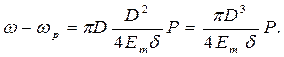
Продифференцировав это выражение по P и рассматривая ω как функцию, зависящую от P, получим:
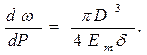
В итоге слагаемое, описывающее упругие свойства материала трубы в выражении для скорости распространения ударной волны, можно представить в следующем виде:
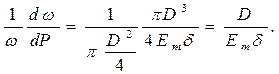
Теперь рассмотрим слагаемое, описывающее упругость жидкости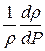 
. Ранее при рассмотрении свойств жидкости было установлено, что если изменение объёма происходит за счёт изменения плотности, то можно определить коэффициент сжимаемости жидкости βw:
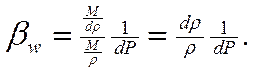
Часто этот коэффициент выражают через обратную величину, называемую модулем упругости жидкости Eж, т. е.:
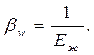
Отсюда следует, что второе слагаемое, характеризующее упругие свойства рабочей среды, может быть представлено в виде:
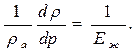
Таким образом, окончательно выражение для скорости распространения ударной волны в упругом трубопроводе можно переписать в следующем виде:
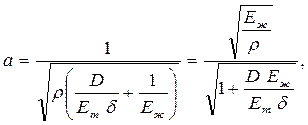
где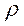 
- плотность жидкости,
D - диаметр трубопровода,
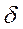- толщина стенки трубопровода,
Ет – объёмный модуль упругости материала трубы,
Еж - объёмный модуль упругости жидкости.
Из формулы следует, что скорость распространения ударной волны зависит от сжимаемости жидкости и упругих деформаций материала трубопровода.
Ударное давление
Для выяснения величины подъёма давления 
Р применим теорему о сохранении количества движения (импульса силы). Для этого рассмотрим элементарное перемещение участка жидкости длинной dL за время dt. Учтём, что при прямом гидроударе кинетическая энергия ударной волны полностью превращается в потенциальную, т.е. скорость жидкости V становится равной нулю 0.
Импульс силы, под действием которого происходит это движение, равен:
.
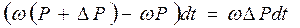Изменение количества движения рассматриваемого объёма длиной dL будет:
,
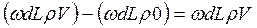Повторимся: скорость во второй скобке равна 0, т.к. рассматриваемый объём жидкости останавливается.
Приравнивая эти выражения по теореме о сохранении количества движения, получим:
.
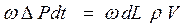Отсюда выразим величину повышения давления ΔP:
.
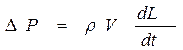После замены дроби скоростью a, окончательно будем иметь:
,
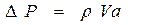где V - скорость жидкости в трубопроводе до возникновения гидроудара,
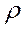- плотность жидкости,
а – скорость распространения ударной волны.
Если в эту формулу подставить выражение описывающее a, то придём к формуле, носящей имя Жуковского:
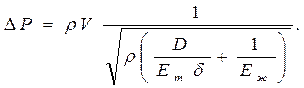
Дата добавления: 2019-10-16; просмотров: 838;