Трехмерный кристалл
Мы рассмотрели колебания в одномерной цепочке. Подобным образом могут быть описаны и колебания решетки трехмерного кристалла.
Предположим, что примитивная ячейка кристалла состоит из l атомов. Каждый атом ячейки будем обозначать индексом s, этот индекс принимает l различных значений. Любой атом кристалла однозначно определяется радиус-вектором 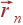 , задающим положение ячейки (соответствующего узла решетки Браве), и индексом s, характеризующим положение атома внутри ячейки (тип атома).
, задающим положение ячейки (соответствующего узла решетки Браве), и индексом s, характеризующим положение атома внутри ячейки (тип атома).
Смещение атомов при колебаниях решетки является линейной комбинацией плоских гармонических волн (точнее, их вещественных частей):
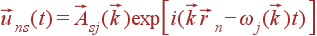
| (40) |
Частота колебаний одинакова для всех атомов кристалла. Амплитуда колебаний зависит от типа атома (индекса s), т. е. одинакова для всех однотипных атомов. Направление вектора амплитуды может, вообще говоря, быть каким угодно.
Индекс j обозначает ветвь колебаний. Волновой вектор 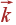 и ветвь j однозначно определяют частоту и относительные амплитуды атомов всех типов. Для каждой ветви зависимости
и ветвь j однозначно определяют частоту и относительные амплитуды атомов всех типов. Для каждой ветви зависимости 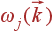 и
и 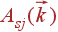 являются непрерывными функциями.
являются непрерывными функциями.
Если примитивная ячейка кристалла содержит l атомов, то число ветвей равно 3l. Таким образом, каждому значению волнового вектора соответствуют 3l разных колебаний.
Три из этих ветвей — акустические, в предельном случае длинных волн их частота пропорциональна длине волнового вектора ω = s|k|. Однако скорость звука s зависит от направления распространения волны, т. е. от направления 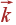 . В случае длинноволновых акустических колебаний амплитуды всех атомов примитивной ячейки примерно одинаковы.
. В случае длинноволновых акустических колебаний амплитуды всех атомов примитивной ячейки примерно одинаковы.
Остальные 3l–3 ветвей — оптические, при 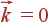 их частота отлична от нуля.
их частота отлична от нуля.
По направлению амплитуды относительно волнового вектора акустические колебания можно разделить на продольное (LA) и два поперечных (TA). Строго говоря, смещения атомов при этих колебаниях параллельны или перпендикулярны вектору 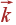 только при распространении волны в направлениях высокой симметрии, например [100] для кристаллов кубической сингонии. Как правило, скорость звука у продольного колебания больше чем у поперечных.
только при распространении волны в направлениях высокой симметрии, например [100] для кристаллов кубической сингонии. Как правило, скорость звука у продольного колебания больше чем у поперечных.
У кристаллов со структурой алмаза или цинковой обманки примитивная ячейка содержит 2 атома. Соответственно, кроме трех акустических, эти кристаллы обладают тремя оптическими ветвями колебаний, из которых также можно выделить продольную (LO) и две поперечных (TO) ветви.
Как и в одномерном случае, волновые вектора, отличающиеся друг от друга на вектор обратной решетки, соответствуют одному и тому же колебанию. По этой причине достаточно рассматривать волновые вектора, лежащие в первой зоне Бриллюэна.
Количество разрешенных волновых векторов в зоне Бриллюэна равно N = V/v0 — числу примитивных ячеек в нормировочном объеме кристалла V = L3 (v0 – объем примитивной ячейки). Действительно, плотность разрешенных волновых векторов в обратном пространстве равна V/(2π)3, т. е. в объеме обратного пространства Δ3k содержится Δ3k· V/(2π)3 разрешенных волновых векторов. Объем зоны Бриллюэна — объем примитивной ячейки обратной решетки — равен (2π)3/v0, и для числа разрешенных состояний получаем (2π)3/v0· V/(2π)3 = V/v0 = N.
Число ветвей — 3l, поэтому полное число колебаний равно 3lN — утроенному числу атомов кристалла в объеме L3, т. е. числу степеней свободы механической системы.
Фононы
Колебаниям решетки, согласно квантовой механике, можно сопоставить квазичастицы — фононы. Каждому колебанию соответствует одно состояние фонона с импульсом 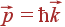 и энергией
и энергией 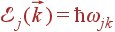 .
.
Фононы являются бозе-частицами: число фононов, соответствующих определенному колебанию (число фононов одном состоянии), может быть сколь угодно большим. В состоянии термодинамического равновесия среднее число фононов njk ветви j с волновым вектором 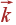 зависит только от энергии фонона (частоты колебания):
зависит только от энергии фонона (частоты колебания):
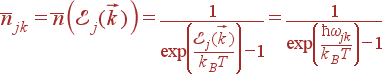
| (41) |
Здесь kB — постоянная Больцмана. С точки зрения квантовой (да и классической) механики, нормальные колебания решетки ведут себя как набор независимых гармонических осцилляторов. Роль координаты осциллятора играет при этом амплитуда колебания, число фононов является уровнем энергии осциллятора.
На каждое колебание приходится средняя энергия 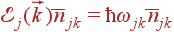 . Строго говоря, к этой энергии надо прибавить энергию основного состояния колебания (энергию нулевых колебаний): как и у обычного гармонического осциллятора она равна
. Строго говоря, к этой энергии надо прибавить энергию основного состояния колебания (энергию нулевых колебаний): как и у обычного гармонического осциллятора она равна  . Но энергией нулевых колебаний кристалл обладает всегда, и мы просто примем ее за начало отсчета.
. Но энергией нулевых колебаний кристалл обладает всегда, и мы просто примем ее за начало отсчета.
При высоких температурах, kb T >> ħω, число фононов пропорционально температуре:
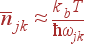
| (42) |
Средняя энергия колебания при этом равна kbT. Это известный результат классической статистической механики для средней энергии гармонического осциллятора. Таким образом, пока температура превосходит энергию фонона, квантовые эффекты не играют роли.
Они играют существенную роль при низких температурах. Если kb T << ħω, то среднее число фононов экспоненциально мало:
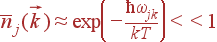
| (43) |
Можно сказать, что колебания, частота которых превосходит величину kbT/ħ, ''вымерзают''. Энергия колебания не может быть меньше энергии одного фонона ħωjk а энергия фонона много больше характерной тепловой энергии kBT, поэтому такие колебания практически не возбуждаются.
Дата добавления: 2019-10-16; просмотров: 578;
