Одномерная цепочка с двумя атомами в примитивной ячейке

Исследуем теперь колебания цепочки, элементарная ячейка которой состоит из двух атомов с разными массами: M₁ и M₂, для определенности положим M₁<M₂. Период цепочки (расстояние между узлами ее решетки Браве) как и прежде обозначим через a (рис. 3). Для простоты будем считать, что ''пружинки'' соединяющие атомы имеют одинаковую жесткость γ.

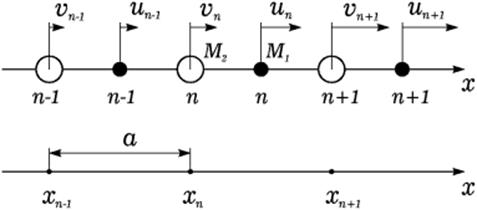Рис. 3. Одномерная цепочка с двумя атомами в примитивной ячейке и ее решетка Браве.

Запишем закон Ньютона для двух атомов n-й ячейки:

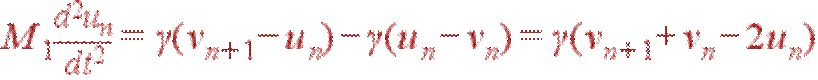
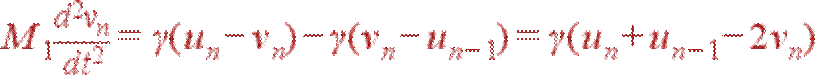
(22)

Здесь u_n и v_n — смещения соответственно маленького и большого атома n-й ячейки из положения равновесия.

Будем, как и в случае цепочки с одним атомом в примитивной ячейке, искать решение в виде плоской гармонической волны:

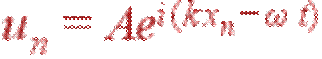
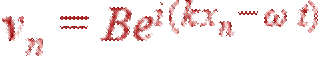
(23)

Амплитуды колебаний маленького и большого атомов A и B в общем случае разные как по абсолютной величине, так и по фазе.

После подстановки (23) в (22) получим линейную однородную систему уравнений для A и B:

Перепишем ее в стандартном виде:

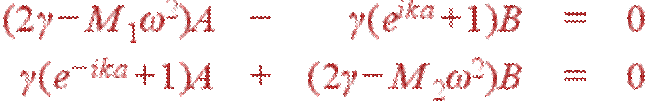
(25)

Такая система имеет решения лишь в том случае, когда ее определитель равен нулю. Приравнивая нулю определитель (25) получим уравнение, связывающее ω и k, т. е. дисперсионное уравнение:

Это уравнение удобно переписать, использую приведенную массу атомов примитивной ячейки μ:

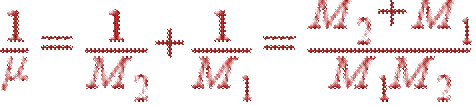
(27)

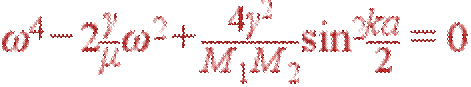
(28)

Его решения имеют вид:

(29)

или

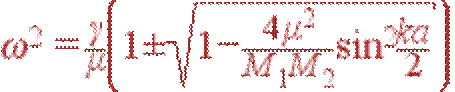
(30)

Величина 4μ²/(M₁M₂) при любых M₁, M₂ не превосходит единицы, поэтому подкоренное выражение всегда неотрицательно.

Итак, для каждого волнового вектора k существуют две частоты ω, удовлетворяющие дисперсионному уравнению. Точнее, есть две непрерывные функции ω(k), которые отличаются знаком перед корнем. Говорят, что существуют две ветви колебаний.

Исследуем обе ветви.

Напомним, что волновые вектора, отличающиеся на вектор обратной решки, описывают одно и то же колебания. (Вследствие этого функция ω(k) периодична с периодом обратной решетки 2π/a, а в трехмерном случае обладает трансляционной симметрией обратной решетки). Поэтому мы считаем, что волновой вектор лежит в пределах первой зоны Бриллюэна: –π/a<k<π/a.

Решение со знаком ''минус''

В точке k = 0:

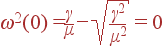
(31)

На границе зоны Бриллюэна:

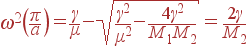
(32)

При ka<< 1 (длинные волны):

ω2(k)	≈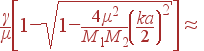
	≈
	=
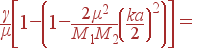
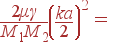
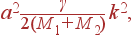
	=		(33)

другими словами

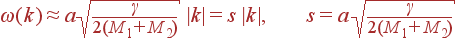
(34)

Мы видим, что в длинноволновом пределе закон дисперсии этой ветви линеен, т. е., как и в случае цепочки с одним атомом в примитивной ячейке, описывает акустические колебания. По этой причине вся ветвь (решение со знаком ''–'') называется акустической (рис. 4).

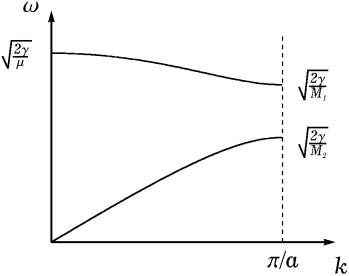Рис. 4. Закон дисперсии колебаний цепочки с двумя атомами в примитивной ячейке.

Выражение для скорости звука имеет такой же вид, что и соответствующее выражение для цепочки с одним атомом в ячейке (20) и зависит от тех же макроскопических характеристик: линейной плотности и упругой постоянной цепочки:

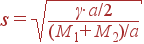
(35)

Линейная плотность двухатомной цепочки равна (M₁+M₂)/a, а упругая постоянная — γ· a/2 (т. к. длина одной пружинки в наших обозначениях равна a/2).

Это и неудивительно. Мы уже видели, изучая цепочку с одним атомом в примитивной ячейке, что длинноволновые акустические колебания можно получить, рассматривая цепочку, как непрерывную упругую среду. Атомы ячейки при таких колебаниях движутся вместе, как единое целое, поэтому структура примитивной ячейки не играет роли, а важны лишь макроскопические, усредненные характеристики цепочки.

То, что атомы ячейки при длинноволновых акустических колебаниях движутся вместе, можно получить и непосредственно, решив систему (25). Эта система разрешима, когда ее определитель равен нулю, а определитель равен нулю, когда ω и k связаны законом дисперсии. При этом уравнения системы уже не являются независимыми, и мы можем взять любое из них, чтобы найти отношение амплитуд A и B.

Из первого уравнения системы (25) получаем:

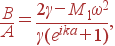
(36)

откуда в пределе длинноволновых акустических колебаний (k→ 0, ω = s |k|→ 0) следует B/A→ 1, т. е. A = B: атомы движутся в фазе с одинаковыми амплитудами.

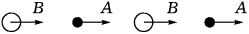Рис. 5. Амплитуды атомов цепочки в случае длинноволновых акустических колебаний.

Отметим также, что на границе зоны Бриллюэна групповая скорость ∂ω/∂ k равна нулю. Это утверждение справедливо для обеих ветвей колебаний.