Множество стабилизирующих управлений
В последние два десятилетия для построения управлений неопределенными объектами интенсивно развивается теория робастного управления. Наибольшие успехи в этой области достигнуты для анализа робастной устойчивости и робастной стабилизации линейных объектов.
Сравнительно недавно теория робастных систем пополнилась новыми инструментами синтеза регуляторов. Для линейных неопределенных систем это алгебраическое неравенство Риккати (Algebraic Riccati Inequality ,АRI), для нелинейных – неравенство Гамильтона-Якоби (Hamilton-Jacoby, HJI) [34,46]. HJI является скалярным неравенством с частными производными, что затрудняет применение этого метода. Одним из возможных способов нахождения робастного управления с использованием HJI является метод, основанный на аппроксимации HJI рядом Тейлора вокруг точки равновесия. Однако метод, основанный на представлении неравенства с частными производными с использованием аппроксимации возле точки равновесия, не позволяет получить более общие решения. С другой стороны, использование нелинейных матричных неравенств дает возможность исследовать системы, параметры которых зависят от состояния. Этот тип нелинейных обыкновенных дифференциальных уравнений позволяет перейти при синтезе робастного управления от использования неравенства Гамильтона-Якоби к неравенству Риккати с параметрами, зависящими от состояния объекта (State Dependent Riccati Inequality, SDRI). Другим словами, если существует положительно определенная матрица 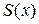 , параметры которой зависят от состояния объекта, и которая удовлетворяет неравенству Риккати (SDRI) и существует положительно определенная скалярная функция
, параметры которой зависят от состояния объекта, и которая удовлетворяет неравенству Риккати (SDRI) и существует положительно определенная скалярная функция 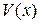 , удовлетворяющая решению
, удовлетворяющая решению 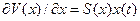 , тогда эта функция удовлетворяет неравенству Гамильтона-Якоби (HJI).
, тогда эта функция удовлетворяет неравенству Гамильтона-Якоби (HJI).
Следует отметить, что использование метода SDRI для решения HJI наталкивается на проблему неоднозначного представления нелинейной системы в форме SDC [43]. Таким образом, решение SDRI может дать различные положительно определенные матрицы 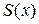 .
.
Добавим, что АRI и HJI невозможно использовать для решения терминальных задач управления неопределенными объектами. В последующих главах будет предложен метод синтеза робастного управления для нелинейного неопределенного объекта с параметрами, зависящими от его состояния (SDC), и заданным временем переходного процесса.
Рассмотрим управляемую и наблюдаемую систему, параметры которой в явном виде не зависят от времени
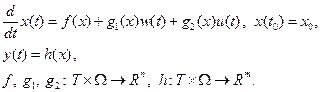 (2.81)
(2.81)
Запишем неравенство Гамильтона-Якоби-Беллмана [42] для системы (2.81)
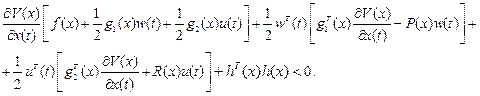 (2.82)
(2.82)
Управления
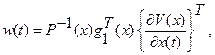
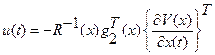 (2.83)
(2.83)
вместе с вектором 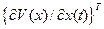 , удовлетворяющем неравенству (2.82), образуют множество управлений стабилизирующих объект (2.81).
, удовлетворяющем неравенству (2.82), образуют множество управлений стабилизирующих объект (2.81).
Пусть объект (2.81) представим в виде
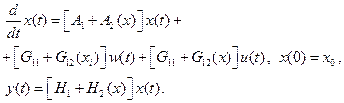 (2.84)
(2.84)
Запишем неравенство (2.82) с учетом (2.84)
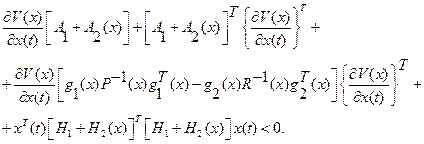 (2.85)
(2.85)
Будем искать 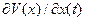 в виде
в виде
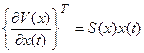 . (2.86)
. (2.86)
Из (2.85) получим
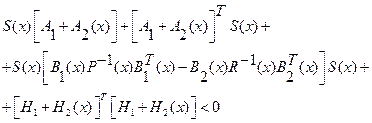 (2.87)
(2.87)
или используя лемму Шура [7,43], преобразуем нелинейное неравенство (2.87) в линейное матричное неравенство
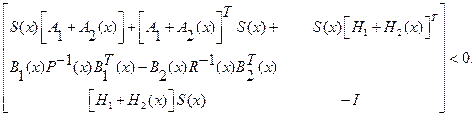 (2.88)
(2.88)
Управления, обеспечивающие стабилизацию системы (2.84), принимают вид
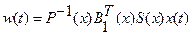 ,
, 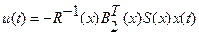 . (2.89)
. (2.89)
Учитывая, что 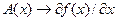 при
при  , значение матрицы
, значение матрицы  в начале координат должно быть таким, чтобы выполнялось неравенство
в начале координат должно быть таким, чтобы выполнялось неравенство
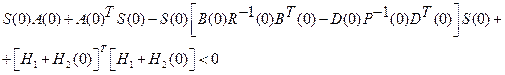 (2.90)
(2.90)
или
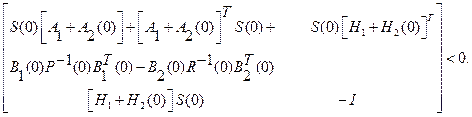 (2.91)
(2.91)
При этом матрицы 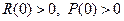 такие, что а матрица
такие, что а матрица
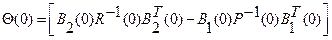 (2.92)
(2.92)
остается, по крайней мере, положительно полуопределенной.
Управления (2.89) с матрицей 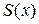 , удовлетворяющей нелинейному матричному неравенству (2.87) или линейному матричному равенству (2.88), образуют множество стабилизируемых воздействий на систему
, удовлетворяющей нелинейному матричному неравенству (2.87) или линейному матричному равенству (2.88), образуют множество стабилизируемых воздействий на систему
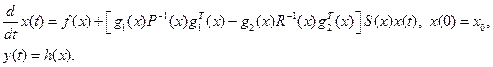 (2.93)
(2.93)
Выводы
Реализация управляющих воздействий для нелинейного объекта, синтезированных SDRE-методом, наталкивается на существенные проблемы, связанные с необходимостью решения нелинейных уравнений с параметрами, зависящими от состояния объекта, в темпе функционирования системы. Наиболее предпочтительным в этой ситуации является использование математических пакетов символических вычислений. Однако в настоящее время это возможно лишь для решения задач управления в простейших постановках (низкая размерность системы, независимость параметров штрафа функционала качества от состояния объекта и пр.). При дискретизации для решения алгебраического уравнения Риккати, если это позволяет делать динамика объекта, можно использование вычислительные процедуры типа Рунге-Кутта. Вычислительные затраты, необходимые для точной реализации SDRE-метода, являются его основным недостатком. Так как вычислительная сложность связана с размерностью системы полиномиальным образом, то с ростом быстродействия вычислительных средств значение этого недостатка постепенно снижается, что подтверждается рядом публикаций [IFAC 2008].
Несмотря на многочисленные примеры, демонстрирующие эффективность SDRE-метода, остается ряд вопросов, связанных с неоднозначностью представления нелинейного объекта в виде модели с линейной структурой и с параметрами, зависящими от состояния. Синтезированные управления с использованием линейной модели и квадратичным критерием качества обеспечивают устойчивость этой модели при любых начальных условиях. Но этого может не быть при приложении синтезированного таким образом управления к нелинейной системе. Таким образом, в общей постановке задачи синтеза не решена задача о глобальной асимптотической устойчивости нелинейной системы с управлением, синтезированным с применением SDRE-метода.
Следует отметить, что основные теоретические достижения в разработке SDRE-метода синтеза управляющих воздействий для нелинейных систем получены при решении задач стабилизации. Круг возможных применений этого метода не ограничивается только такими задачами.
Дата добавления: 2019-10-16; просмотров: 378;
