Свойства растворов полимеров
Рассмотрим теперь случаи, когда в полимер вводится низкомолекулярный растворитель:
а) расплав разбавляется растворителем;
б) добавляем различное количество полимера в растворитель, образуются растворы полимера с различной концентрацией.
В этом случае можно, изучая свойства раствора, определять различные характеристики клубков полимерных молекул. При увеличении концентрации полимера клубки начинают взаимодействовать друг с другом, при дальнейшем увеличении концентрации клубки начинают переплетаться.
В растворах полимеров могут реализовываться несколько областей состояния:
1. в разбавленных растворах полимеров клубки макромолекул изолированы друг от друга;
2. в полуразбавленных растворах начинается соприкосновение клубков и их проникновение друг в друга;
3. в концентрированных растворах полимеров степень проникновения клубков друг в друга довольно велика.
Для описания растворов полимеров можно использовать различные теории – теории Флори, Флори-Хаггинса, Де Жена.
В настоящее время для изучения вязкости растворов применяется нахождение степенной зависимости между вязкостью раствора и концентрацией полимера в нем (точные расчеты проводятся редко).
Согласно уравнению Эйнштейна, вязкость раствора полимера зависит от объемной доли частиц в нем следующим образом:
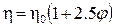 , (20.1.1)
, (20.1.1)
где 2,5 – коэффициент формы частицы (в данном случае частицы сферические).
Объемную долю частиц полимера в растворе можно выразить через концентрации этих частиц. Соответственно, с увеличением концентрации частиц и их объемная доля в растворе будет увеличиваться. Получаем, что с ростом концентрации частиц вязкость должна возрастать линейно. Это действительно наблюдается в некоторой области концентраций. Но при достижении некоторой концентрации с* происходит излом:
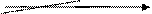 lgη
lgη
tgβ=3.5
β
tgα=1
α
lg с* lgс
Рис. 20.1.1. Зависимость вязкости от концентрации полимера в растворе
Область с tgα=1 является областью разбавленных растворов, в которых клубки макромолекул практически не сопротивляются, они как бы изолированы в пространстве и не взаимодействуют друг с другом. Эта область концентраций используется для изучения размеров и свойств клубков макромолекул. Выше концентрации с* наблюдается резкий излом, мы переходим к полуразбавленным растворам. Далее растворы становятся концентрированными (тангенс наклона кривой увеличивается). Значение критической концентрации с* связано с характеристической вязкостью:

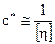 (20.1.2)
(20.1.2)
Характеристическая вязкость [η] представляет объем изолированного клубка.
Таким образом, при с=с* весь объем раствора заполнен клубками макромолекул, которые практически не проникают друг в друга.
Для изучения свойств растворов полимеров можно использовать явление осмоса. Т.к. растворы равновесны, то можно применить уравнения состояния:
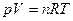 (для газов) (20.1.3)
(для газов) (20.1.3)
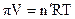 (для жидкостей) (20.1.4)
(для жидкостей) (20.1.4)
При образовании растворов химический потенциал понижается:
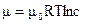 , (20.1.5)
, (20.1.5)
появляется движущая сила перехода растворителя в раствор.
Растворенное Полупроницаемая растворитель
вещество мембрана
Рис. 20.1.2. Явление осмоса
Если разделить растворитель и раствор полупроницаемой мембраной, то сначала уровни жидкости будут одинаковы, затем происходит миграция растворителя через мембрану из-за возникающей разности термодинамических потенциалов растворителя в чистом растворителе и в растворе, образуется разность уровней жидкости Δh. При этом возникшее гидростатическое давление уравновешивает разность осмотических давлений растворителя в ячейках. Измеряя Δh можно определить осмотическое давление растворителя.
Принимая раствор идеальным можно записать соотношение:
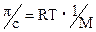 (20.1.6)
(20.1.6)
Для реальных растворов применим закон Ван-дер-ваальса:
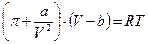 , (20.1.7)
, (20.1.7)
где а – константа сцепления, b – константа отталкивания.
Эту зависимость разлагают в ряд:
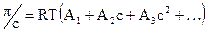 , (20.1.8)
, (20.1.8)
где 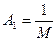 ,
, 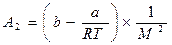 (20.1.9)
(20.1.9)
слагаемыми высших порядков пренебрегают. Второе слагаемое показывает все парные взаимодействия; третий член - тройные взаимодействия, роль которых в общей картине незначительна, ими пренебрегают; взаимодействия более трех частиц одновременно друг с другом очень маловероятно, ими также пренебрегают.
т. е. 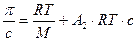 (20.1.10)
(20.1.10)
Существует некоторая температура, называемая тета-температурой (θ) при которой А2=0. В этой точке силы сцепления и отталкивания точно компенсируют друг друга, а раствор ведет себя как идеальный. Можно подобрать θ-растворитель, в котором А2=0. При Т = θ, А2 = 0, т. е.: 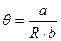 (20.1.11)
(20.1.11)
В зависимости от взятого растворителя могут наблюдаться различные случаи взаимодействия полимера с растворителем:

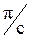
А2>0
А2=0

А2<0
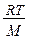
c
Рис. 20.1.3. Случаи взаимодействия полимера с растворителем
Если А2>0, то растворитель считается "хорошим" (полимер хорошо растворим в растворителе, клубки макромолекул в растворе достаточно развернутые); если А2<0, то растворитель считается "плохим" (в нем полимер либо вообще не растворим, либо растворим ограниченно в узком интервале концентраций), либо образуемые растворы неустойчивы, клубки макромолекул в таких растворах сжаты); если А2 = 0, то макромолекулы имеют невозмущенную θ-конформацию.
Таким образом, термодинамическое состояние клубков определяется растворителем.
Рассмотрим вязкость разбавленных растворов полимеров.
Выше было рассмотрено уравнение Эйнштейна:
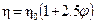 (20.1.12)
(20.1.12)
и вводилось понятие характеристической вязкости, которая представляется в виде:
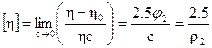 (20.1.13)
(20.1.13)
Из этого выражения следует, что величина [η] не должна зависеть от молекулярной массы полимера, а лишь от его плотности (в растворе).
Однако, реальная зависимость характеристической вязкости от молекулярной массы растворенного полимера является степенной:
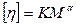 (20.1.14)
(20.1.14)
-это выражение носит название уравнение Марка-Куна-Хаувинка.
Из этого полуэмпирического уравнения следует, что характеристическая вязкость не зависит от молекулярной массы полимера только при α=0, при α≠0 зависимость от молекулярной массы существует в любом случае. Покажем, что это вытекает из рассмотрения конформации макромолекулярных клубков и занимаемого ими объема.
Принимаем, что клубки имеют сферическую форму, тогда:
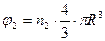 , (20.1.15)
, (20.1.15)
отсюда получим, что
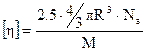 (20.1.16)
(20.1.16)
Т. к. радиус клубка
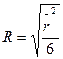 , (20.1.17)
, (20.1.17)
то 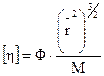 , (20.1.18)
, (20.1.18)
где Ф – комплексная константа. Полученное уравнение называется уравнением Флори-Фокса. Его можно привести к виду уравнения Марка-Куна-Хаувинка. Т. к. радиус клубка зависит от ММ макромолекулы, то справедливо соотнести оба полученных уравнения:
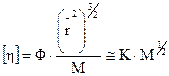 , (20.1.19)
, (20.1.19)
где К является константой для данной системы полимер-растворитель. Получаем, что по теории Флори-Фокса степенной коэффициент α должен быть равен ½.
В действительности, α=1/2 описывает растворы в θ-точке (т.е. поведение макромолекул в θ-растворителе). В "хорошем" растворителе α>0,5 (обычно находится в интервале 0,6÷0,8, хотя может достигать 1 и более – для растворов полимеров, в которых макромолекулы представляют собой "палочки" или длинные плавно изогнутые цепи). В плохом же растворителе α<0,5 (обычно находится в интервале 0,2÷0,4). Случай, в котором α=0 характерен для сильно разветвленных или глобулярных молекул, поэтому в большинстве случаев характеристическая вязкость зависит от молекулярной массы макромолекулы.
Дата добавления: 2019-07-26; просмотров: 1195;
