Монотонные последовательности, число e

Мы доказываем теорему о свойствах пределов. Пусть 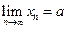, , 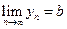тогда 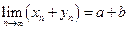, , 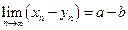, 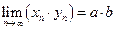а если, кроме того, 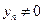, , 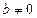то .

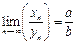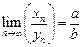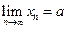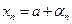Доказательство формулы . Мы докажем, что предел частного последовательностей равен частному от их пределов, если каждый из пределов существует, все числа в знаменателе не равны 0 и предел знаменателя не равен 0. Так как , то , где 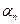- б. м. Аналогично 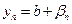, где 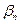- б. м. Отсюда следует, что 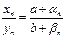. Для доказательства формулы достаточно доказать, что величина 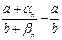является б. м. Проверим, что величина 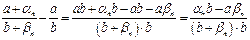является б. м. В самом деле, легко проверить, что в полученном выражении числитель стремится к 0, а знаменатель по модулю больше некоторого положительного числа. Формула доказана.

Пример 1. Найдите пределы числовых последовательностей ( ):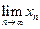

а) 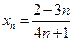, 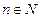; б) , ;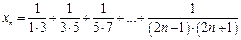

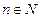Решение. а) Докажем, что 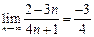. В самом деле, , т. е. 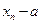является б. м. величиной. Можно доказать, что отношение многочленов равно 0, если степень числителя меньше степени знаменателя; равно бесконечности (является б. б.), если степень числителя больше степени знаменателя; равно отношению коэффициентов при старших степенях, если степень числителя равна степени знаменателя.

б) Докажем, что 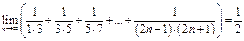. В самом деле, 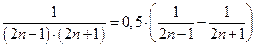, поэтому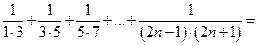 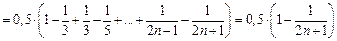. Полученная величина отличается от 0,5 на б. м. величину.