Но это только техническая сторона. Очень важна и другая — способы использования компьютеров, стиль программирования, особенности математического обеспечения.

Перфокарта
Программы для этих машин писались на языке конкретной машины. Математик, составивший программу, садился за пульт управления машины, вводил и отлаживал программы и производил по ним счет. Процесс отладки был наиболее длительным по времени.
Несмотря на ограниченность возможностей, эти машины позволили выполнить сложнейшие расчёты, необходимые для прогнозирования погоды, решения задач атомной энергетики и др.
Опыт использования машин первого поколения показал, что существует огромный разрыв между временем, затрачиваемым на разработку программ, и временем счета.

ЭВМ "Урал"
Эти проблемы начали преодолевать путем интенсивной разработки средств автоматизации программирования, создания систем обслуживающих программ, упрощающих работу на машине и увеличивающих эффективность её использования. Это, в свою очередь, потребовало значительных изменений в структуре компьютеров, направленных на то, чтобы приблизить её к требованиям, возникшим из опыта эксплуатации компьютеров.
Отечественные машины первого поколения: МЭСМ (малая электронная счётная машина), БЭСМ, Стрела, Урал, М—20.
3.5. Какие компьютеры относятся ко второму поколению?

БЭСМ—6. Второе поколение

Транзистор
Второе поколение компьютерной техники — машины, сконструированные примерно в 1955—65 гг. Характеризуются использованием в них как электронных ламп, так и дискретных транзисторных логических элементов. Их оперативная память была построена на магнитных сердечниках. В это время стал расширяться диапазон применяемого оборудования ввода-вывода, появились высокопроизводительные устройства для работы с магнитными лентами, магнитные барабаны и первые магнитные диски.

Память на магнитных
сердечниках
Быстродействие — до сотен тысяч операций в секунду, ёмкость памяти — до нескольких десятков тысяч слов.
Появились так называемые языки высокого уровня, средства которых допускают описание всей необходимой последовательности вычислительных действий в наглядном, легко воспринимаемом виде.
Программа, написанная на алгоритмическом языке, непонятна компьютеру, воспринимающему только язык своих собственных команд. Поэтому специальные программы, которые называются трансляторами, переводят программу с языка высокого уровня на машинный язык.
Появился широкий набор библиотечных программ для решения разнообразных математических задач. Появились мониторные системы, управляющие режимом трансляции и исполнения программ. Из мониторных систем в дальнейшем выросли современные операционные системы.
| Операционная система — важнейшая часть программного обеспечения компьютера, предназначенная для автоматизации планирования и организации процесса обработки программ, ввода-вывода и управления данными, распределения ресурсов, подготовки и отладки программ, других вспомогательных операций обслуживания. |
Таким образом, операционная система является программным расширением устройства управления компьютера.
Для некоторых машин второго поколения уже были созданы операционные системы с ограниченными возможностями.
Машинам второго поколения была свойственна программная несовместимость, которая затрудняла организацию крупных информационных систем. Поэтому в середине 60-х годов наметился переход к созданию компьютеров, программно совместимых и построенных на микроэлектронной технологической базе.
3.6. В чем особенности компьютеров третьего поколения?

Компьютер IBM—360.
Третье поколение
Машины третьего поколения созданы примерно после 60-x годов. Поскольку процесс создания компьютерной техники шел непрерывно, и в нём участвовало множество людей из разных стран, имеющих дело с решением различных проблем, трудно и бесполезно пытаться установить, когда "поколение" начиналось и заканчивалось. Возможно, наиболее важным критерием различия машин второго и третьего поколений является критерий, основанный на понятии архитектуры.

Интегральная схема
Машины третьего поколения — это семейства машин с единой архитектурой, т.е. программно совместимых. В качестве элементной базы в них используются интегральные схемы, которые также называются микросхемами.
Машины третьего поколения имеют развитые операционные системы. Они обладают возможностями мультипрограммирования, т.е. одновременного выполнения нескольких программ. Многие задачи управления памятью, устройствами и ресурсами стала брать на себя операционная система или же непосредственно сама машина.
Примеры машин третьего поколения — семейства IBM—360, IBM—370, ЕС ЭВМ (Единая система ЭВМ), СМ ЭВМ (Семейство малых ЭВМ) и др.
Быстродействие машин внутри семейства изменяется от нескольких десятков тысяч до миллионов операций в секунду. Ёмкость оперативной памяти достигает нескольких сотен тысяч слов.
| Краткое описание процесса изготовления микросхем |
|
3.7. Что характерно для машин четвёртого поколения?
Четвёртое поколение — это теперешнее поколение компьютерной техники, разработанное после 1970 года.
Наиболее важный в концептуальном отношении критерий, по которому эти компьютеры можно отделить от машин третьего поколения, состоит в том, что машины четвёртого поколения проектировались в расчете на эффективное использование современных высокоуровневых языков и упрощение процесса программирования для конечного пользователя.
В аппаратурном отношении для них характерно широкое использование интегральных схем в качестве элементной базы, а также наличие быстродействующих запоминающих устройств с произвольной выборкой ёмкостью в десятки мегабайт.
C точки зрения структуры машины этого поколения представляют собой многопроцессорные и многомашинные комплексы, работающие на общую память и общее поле внешних устройств. Быстродействие составляет до нескольких десятков миллионов операций в секунду, ёмкость оперативной памяти порядка 1 — 64 Мбайт.
Для них характерны:
- применение персональных компьютеров;
- телекоммуникационная обработка данных;
- компьютерные сети;
- широкое применение систем управления базами данных;
- элементы интеллектуального поведения систем обработки данных и устройств.
3.8. Какими должны быть компьютеры пятого поколения?
Разработка последующих поколений компьютеров производится на основе больших интегральных схем повышенной степени интеграции, использования оптоэлектронных принципов (лазеры,голография).
Развитие идет также по пути "интеллектуализации" компьютеров, устранения барьера между человеком и компьютером. Компьютеры будут способны воспринимать информацию с рукописного или печатного текста, с бланков, с человеческого голоса, узнавать пользователя по голосу, осуществлять перевод с одного языка на другой.
| В компьютерах пятого поколения произойдёт качественный переход от обработки данных к обработке знаний. |
Архитектура компьютеров будущего поколения будет содержать два основных блока. Один из них — это традиционный компьютер. Но теперь он лишён связи с пользователем. Эту связь осуществляет блок, называемый термином "интеллектуальный интерфейс". Его задача — понять текст, написанный на естественном языке и содержащий условие задачи, и перевести его в работающую программу для компьютера.
Будет также решаться проблема децентрализации вычислений с помощью компьютерных сетей, как больших, находящихся на значительном расстоянии друг от друга, так и миниатюрных компьютеров, размещённых на одном кристалле полупроводника.
3.10. На какие типы делятся компьютеры по производительности и характеру использования?
По производительности и характеру использования компьютеры можно условно подразделить на:
- микрокомпьютеры, в том числе — персональные компьютеры;
- миникомпьютеры;
- мэйнфреймы (универсальные компьютеры);
- суперкомпьютеры.
Микрокомпьютеры — это компьютеры, в которых центральный процессор выполнен в виде микропроцессора.
Продвинутые модели микрокомпьютеров имеют несколько микропроцессоров. Производительность компьютера определяется не только характеристиками применяемого микропроцессора, но и ёмкостью оперативной памяти, типами периферийных устройств, качеством конструктивных решений и др.
Микрокомпьютеры представляют собой инструменты для решения разнообразных сложных задач. Их микропроцессоры с каждым годом увеличивают мощность, а периферийные устройства — эффективность. Быстродействие — порядка 1 — 10 миллионов опеpаций в сек.
Разновидность микрокомпьютера — микроконтроллер. Это основанное на микропроцессоре специализированное устройство, встраиваемое в систему управления или технологическую линию.
| Персональные компьютеры (ПК) — это микрокомпьютеры универсального назначения, рассчитанные на одного пользователя и управляемые одним человеком. |
В класс персональных компьютеров входят различные машины — от дешёвых домашних и игровых с небольшой оперативной памятью, с памятью программы на кассетной ленте и обычным телевизором в качестве дисплея (80-е годы), до сверхсложных машин с мощным процессором, винчестерским накопителем ёмкостью в десятки Гигабайт, с цветными графическими устройствами высокого разрешения, средствами мультимедиа и другими дополнительными устройствами.
Пеpсональный компьютеp должен удовлетворять следующим требованиям:
- стоимост от нескольких сотен до 5 —10 тыс. долларов;
- наличие внешних ЗУ на магнитных дисках;
- объём оперативной памяти не менее 32 Мбайт;
- наличие операционной системы;
- способность работать с программами на языках высокого уровня;
- ориентация на пользователя-непрофессионала (в простых моделях).
Миникомпьютерами и суперминикомпьютерами называются машины, конструктивно выполненные в одной стойке, т.е. занимающие объём порядка половины кубометра. Сейчас компьютеры этого класса вымирают, уступая место микрокомпьютерам.
Мэйнфреймы предназначены для решения широкого класса научно-технических задач и являются сложными и дорогими машинами. Их целесообразно применять в больших системах при наличии не менее 200 — 300 рабочих мест.
Централизованная обработка данных на мэйнфрейме обходится примерно в 5 — 6 раз дешевле, чем распределённая обработка при клиент-серверном подходе.
Известный мэйнфрейм S/390 фирмы IBM обычно оснащается не менее чем тремя процессорами. Максимальный объём оперативного хранения достигает 342 Терабайт.
Производительность его процессоров, пропускная способность каналов, объём оперативного хранения позволяют наращивать число рабочих мест в диапазоне от 20 до 200000 с помощью простого добавления процессорных плат, модулей оперативной памяти и дисковых накопителей.
Десятки мэйнфреймов могут работать совместно под управлением одной операционной системы над выполнением единой задачи.

Суперкомпьютер CRAY —1
Суперкомпьютеры — это очень мощные компьютеры с производительностью свыше 100 мегафлопов (1 мегафлоп — миллион операций с плавающей точкой в секунду). Они называются сверхбыстродействующими. Эти машины представляют собой многопроцессорные и (или) многомашинные комплексы, работающие на общую память и общее поле внешних устройств. Различают суперкомпьютеры среднего класса, класса выше среднего и переднего края (high end).
Архитектура суперкомпьютеров основана на идеях параллелизма и конвейеризации вычислений.
В этих машинах параллельно, то есть одновременно, выполняется множество похожих операций (это называется мультипроцессорной обработкой). Таким образом, сверхвысокое быстродействие обеспечивается не для всех задач, а только для задач, поддающихся распараллеливанию.
Что такое конвейеpная обработка? Приведем сравнение — на каждом рабочем месте конвейера выполняется один шаг производственного процесса, а на всех рабочих местах в одно и то же время обрабатываются различные изделия на всевозможных стадиях. По такому принципу устроено арифметико-логическое устройство суперкомпьютера.
Отличительной особенностью суперкомпьютеров являются векторные процессоры, оснащенные аппаратурой для параллельного выполнения операций с многомерными цифровыми объектами — векторами и матрицами. В них встроены векторные регистры и параллельный конвейерный механизм обработки. Если на обычном процессоре программист выполняет операции над каждым компонентом вектора по очереди, то на векторном — выдаёт сразу векторые команды.
Векторная аппаратура очень дорога, в частности, потому, что требуется много сверхбыстродействующей памяти под векторные регистры.
Наиболее распространённые суперкомпьютеры — массово-параллельные компьютерные системы. Они имеют десятки тысяч процессоров, взаимодействующих через сложную, иерархически организованую систему памяти.
В качестве примера рассмотрим характеристики многоцелевого массово-параллельного суперкомпьютера среднего класса Intel Pentium Pro 200. Этот компьютер содержит 9200 процессоров Pentium Pro на 200 Мгц, в сумме (теоретически) обеспечивающих производительность 1,34 Терафлоп (1 Терафлоп равен 1012 операций с плавающей точкой в секунду), имеет 537 Гбайт памяти и диски ёмкостью 2,25 Терабайт. Система весит 44 тонны (кондиционеры для неё — целых 300 тонн) и потребляет мощность 850 кВт.
Супер-компьютеры используются для решения сложных и больших научных задач (метеорология, гидродинамика и т. п.), в управлении, разведке, в качестве централизованных хранилищ информации и т.д.
Элементная база — микросхемы сверхвысокой степени интеграции.
3.11. Какие существуют типы портативных компьютеров?
Портативные компьютеры обычно нужны руководителям предприятий, менеджерам, учёным, журналистам, которым приходится работать вне офиса — дома, на презентациях или во время командировок.
Основные разновидности портативных компьютеров:

Laptop
Laptop (наколенник, от lap> — колено и top — поверх). По размерам близок к обычному портфелю. По основным характеристикам (быстродействие, память) примерно соответствует настольным ПК. Сейчас компьютеры этого типа уступают место ещё меньшим.

Notebook
Notebook (блокнот, записная книжка). По размерам он ближе к книге крупного формата. Имеет вес около 3 кг. Помещается в портфель-дипломат. Для связи с офисом его обычно комплектуют модемом. Ноутбуки зачастую снабжают приводами CD—ROM.
Многие современные ноутбуки включают взаимозаменяемые блоки со стандартными разъёмами. Такие модули предназначены для очень разных функций. В одно и то же гнездо можно по мере надобности вставлять привод компакт-дисков, накопитель на магнитных дисках, запасную батарею или съёмный винчестер. Ноутбук устойчив к сбоям в энергопитании. Даже если он получает энергию от обычной электросети, в случае какого-либо сбоя он мгновенно переходит на питание от аккумуляторов.

Palmtop

Персональный
цифровой помощник
Palmtop (наладонник) — самые маленькие современные персональные компьютеры. Умещаются на ладони. Магнитные диски в них заменяет энергонезависимая электронная память. Нет и накопителей на дисках — обмен информацией с обычными компьютерами идет линиям связи. Если Palmtop дополнить набором деловых программ, записанных в его постоянную память, получится персональный цифровой помощник (Personal Digital Assistant).
Карманный компьютер
iPAQ 3150
Возможности портативных компьютеров постоянно расширяются. Например, современный карманный компьютер iPAQ 3150 располагает всем необходимым для: ведения списка задач, хранения записок, включая аудиофайлы, работы с календарем, чтения электронной почты, синхронизации с РС, мобильным телефоном. Помимо этого iPAQ позволяет: проигрывать видео и звуковые ролики, бродить по Интернету, просматривать и редактировать документы и электронные таблицы, хранить файлы, искать в них слова, просматривать картинки вести домашнюю бухгалтерию, играть в игры, читать электронные книги с помощью Microsoft Reader, полноценно работать с программным обеспечением.
4.1. Что такое система счисления?
| Система счисления — это совокупность приемов и правил, по которым числа записываются и читаются. |
Существуют позиционные и непозиционные системы счисления.
В непозиционных системах счисления вес цифры (т. е. тот вклад, который она вносит в значение числа) не зависит от ее позициив записи числа. Так, в римской системе счисления в числе ХХХII (тридцать два) вес цифры Х в любой позиции равен просто десяти.
В позиционных системах счисления вес каждой цифры изменяется в зависимости от ее положения (позиции) в последовательности цифр, изображающих число. Например, в числе 757,7 первая семерка означает 7 сотен, вторая — 7 единиц, а третья — 7 десятых долей единицы.
Сама же запись числа 757,7 означает сокращенную запись выражения
700 + 50 + 7 + 0,7 = 7 . 102 + 5 . 101 + 7 . 100 + 7 . 10-1 = 757,7.
Любая позиционная система счисления характеризуется своим основанием.
| Основание позиционной системы счисления — количество различных цифр, используемых для изображения чисел в данной системе счисления. |
За основание системы можно принять любое натуральное число — два, три, четыре и т.д. Следовательно, возможно бесчисленное множество позиционных систем: двоичная, троичная, четверичная и т.д. Запись чисел в каждой из систем счисления с основанием q означает сокращенную запись выражения
an-1 qn-1 + an-2 qn-2 + ... + a1 q1 + a0 q0 + a-1 q-1 + ... + a-m q-m,
где ai — цифры системы счисления; n и m — число целых и дробных разрядов, соответственно.
Например:
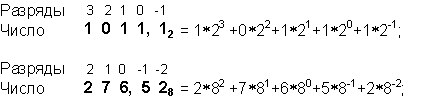
4.2. Как порождаются целые числа в позиционных системах счисления?
В каждой системе счисления цифры упорядочены в соответствии с их значениями: 1 больше 0, 2 больше 1 и т.д.
| Продвижением цифры называют замену её следующей по величине. |
Продвинуть цифру 1 значит заменить её на 2, продвинуть цифру 2 значит заменить её на 3 и т.д. Продвижение старшей цифры (например, цифры 9 в десятичной системе) означает замену её на 0. В двоичной системе, использующей только две цифры — 0 и 1, продвижение 0 означает замену его на 1, а продвижение 1 — замену её на 0.
Целые числа в любой системе счисления порождаются с помощью Правила счета:
| Для образования целого числа, следующего за любым данным целым числом, нужно продвинуть самую правую цифру числа; если какая-либо цифра после продвижения стала нулем, то нужно продвинуть цифру, стоящую слева от неё. |
Применяя это правило, запишем первые десять целых чисел
- в двоичной системе: 0, 1, 10, 11, 100, 101, 110, 111, 1000, 1001;
- в троичной системе: 0, 1, 2, 10, 11, 12, 20, 21, 22, 100;
- в пятеричной системе: 0, 1, 2, 3, 4, 10, 11, 12, 13, 14;
- в восьмеричной системе: 0, 1, 2, 3, 4, 5, 6, 7, 10, 11.
4.3. Какие системы счисления используют специалисты для общения с компьютером?
Кроме десятичной широко используются системы с основанием, являющимся целой степенью числа 2, а именно:
- двоичная (используются цифры 0, 1);
- восьмеричная (используются цифры 0, 1, ..., 7);
- шестнадцатеричная (для первых целых чисел от нуля до девяти используются цифры 0, 1, ..., 9, а для следующих чисел — от десяти до пятнадцати — в качестве цифр используются символы A, B, C, D, E, F).
Полезно запомнить запись в этих системах счисления первых двух десятков целых чисел:
|
|
Из всех систем счисления особенно проста и поэтому интересна для технической реализации в компьютерах двоичная система счисления.
4.4. Почему люди пользуются десятичной системой, а компьютеры — двоичной?
Люди предпочитают десятичную систему, вероятно, потому, что с древних времен считали по пальцам, а пальцев у людей по десять на руках и ногах. Не всегда и не везде люди пользуются десятичной системой счисления. В Китае, например, долгое время пользовались пятеричной системой счисления.
А компьютеры используют двоичную систему потому, что она имеет ряд преимуществ перед другими системами:
- для ее реализации нужны технические устройства с двумя устойчивыми состояниями (есть ток — нет тока, намагничен — не намагничен и т.п.), а не, например, с десятью, — как в десятичной;
- представление информации посредством только двух состояний надежно и помехоустойчиво;
- возможно применение аппарата булевой алгебры для выполнения логических преобразований информации;
- двоичная арифметика намного проще десятичной.
4.5. Почему в компьютерах используются также восьмеричная и шестнадцатеричная системы счисления?
Двоичная система, удобная для компьютеров, для человека неудобна из-за ее громоздкости и непривычной записи.
Перевод чисел из десятичной системы в двоичную и наоборот выполняет машина. Однако, чтобы профессионально использовать компьютер, следует научиться понимать слово машины. Для этого и разработаны восьмеричная и шестнадцатеричная системы.
Числа в этих системах читаются почти так же легко, как десятичные, требуют соответственно в три (восьмеричная) и в четыре (шестнадцатеричная) раза меньше разрядов, чем в двоичной системе (ведь числа 8 и 16 — соответственно, третья и четвертая степени числа 2).
| Перевод восьмеричных и шестнадцатеричных чисел в двоичную систему очень прост: достаточно каждую цифру заменить эквивалентной ей двоичной триадой (тройкой цифр) или тетрадой (четверкой цифр). |
Например:

| Чтобы перевести число из двоичной системы в восьмеричную или шестнадцатеричную, его нужно разбить влево и вправо от запятой на триады (для восьмеричной) или тетрады (для шестнадцатеричной) и каждую такую группу заменить соответствующей восьмеричной (шестнадцатеричной) цифрой. |
Например,
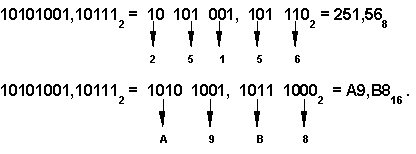
писи чисел. 4.6. Как перевести целое число из десятичной системы в любую другую позиционную систему счисления?
| Для перевода целого десятичного числа N в систему счисления с основанием q необходимо N разделить с остатком ("нацело") на q , записанное в той же десятичной системе. Затем неполное частное, полученное от такого деления, нужно снова разделить с остатком на q , и т.д., пока последнее полученное неполное частное не станет равным нулю. Представлением числа N в новой системе счисления будет последовательность остатков деления, изображенных одной q-ичной цифрой и записанных в порядке, обратном порядку их получения. |
Пример: Переведем число 75 из десятичной системы в двоичную, восьмеричную и шестнадцатеричную:
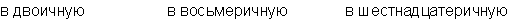
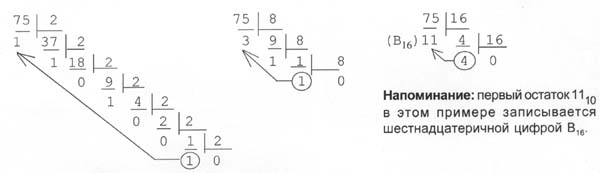
Ответ: 7510 = 1 001 0112 = 1138 = 4B16.
4.7. Как пеpевести пpавильную десятичную дpобь в любую другую позиционную систему счисления?
| Для перевода правильной десятичной дpоби F в систему счисления с основанием q необходимо F умножить на q , записанное в той же десятичной системе, затем дробную часть полученного произведения снова умножить на q, и т. д., до тех пор, пока дpобная часть очередного пpоизведения не станет pавной нулю, либо не будет достигнута требуемая точность изображения числа F в q-ичной системе. Представлением дробной части числа F в новой системе счисления будет последовательность целых частей полученных произведений, записанных в порядке их получения и изображенных одной q-ичной цифрой. Если требуемая точность перевода числа F составляет k знаков после запятой, то предельная абсолютная погрешность при этом равняется q -(k+1) / 2. |
Пример. Переведем число 0,36 из десятичной системы в двоичную, восьмеричную и шестнадцатеричную:

| Для чисел, имеющих как целую, так и дробную части, перевод из десятичной системы счисления в другую осуществляется отдельно для целой и дробной частей по правилам, указанным выше. |
4.8. Как пеpевести число из двоичной (восьмеpичной, шестнадцатеpичной) системы в десятичную?
| Перевод в десятичную систему числа x, записанного в q-ичной cистеме счисления (q = 2, 8 или 16) в виде xq = (anan-1 ... a0 , a-1 a-2 ... a-m)q сводится к вычислению значения многочлена x10 = an qn + an-1 qn-1 + ... + a0 q0 + a-1 q -1 + a-2 q-2 + ... + a-m q-m средствами десятичной арифметики. |
Примеpы:

Сводная таблица переводов целых чисел из одной системы счисления в другую
Рассмотрим только те системы счисления, которые применяются в компьютерах — десятичную, двоичную, восьмеричную и шестнадцатеричную. Для определенности возьмем произвольное десятичное число, например 46, и для него выполним все возможные последовательные переводы из одной системы счисления в другую. Порядок переводов определим в соответствии с рисунком:
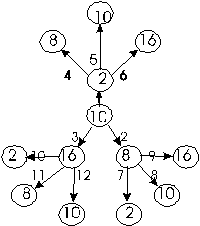
На этом рисунке использованы следующие обозначения:
- в кружках записаны основания систем счисления;
- стрелки указывают направление перевода;
- номер рядом со стрелкой означает порядковый номер соответствующего примера в сводной таблице 4.1.
Например: 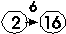 означает перевод из двоичной системы в шестнадцатеричную, имеющий в таблице порядковый номер 6.
означает перевод из двоичной системы в шестнадцатеричную, имеющий в таблице порядковый номер 6.
Сводная таблица переводов целых чисел
Таблица 4.1.


4.10. Как производятся арифметические операции в позиционных системах счисления?
Рассмотрим основные арифметические операции: сложение, вычитание, умножение и деление. Правила выполнения этих операций в десятичной системе хорошо известны — это сложение, вычитание, умножение столбиком и деление углом. Эти правила применимы и ко всем другим позиционным системам счисления. Только таблицами сложения и умножения надо пользоваться особыми для каждой системы.
С л о ж е н и е
Таблицы сложения легко составить, используя Правило Счета.
Сложение в двоичной системе

| Сложение в восьмеричной системе

|
Дата добавления: 2019-07-26; просмотров: 982;
