Изоморфизм групп. Порядок элемента в группе.
Определение 14.1. Пусть 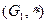 и
и 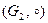 – группы. Биективное отображение
– группы. Биективное отображение 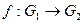 , при котором для любых
, при котором для любых 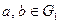 выполняется соотношение
выполняется соотношение

называется изоморфизмом групп и обозначается 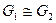 .
.
Лемма 14.1. Бинарное отношение изоморфизма групп есть отношение эквивалентности на множестве всех групп.
Доказательство. Простое упражнение.
Свойства изоморфизма групп.
Пусть группы в определении 14.1 мультипликативны и изоморфны с изоморфизмом 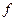 . Тогда
. Тогда
1. 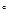
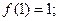
2. 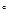
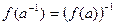 ;
;
3. 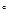
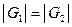 ;
;
4 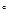 Изоморфный образ группы (подгруппы) есть группа (подгруппа).
Изоморфный образ группы (подгруппы) есть группа (подгруппа).
Докажем, например, свойство 2 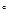 . Имеем
. Имеем
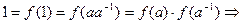
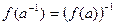 .
.
В дальнейшем будут указаны и другие свойства изоморфизма. Рассмотрим некоторые примеры.
Пример 14.1. Если в примере 1.31 с треугольником из первой главы вершины перенумеровать номерами 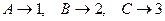 , то отображения из множества Ф
, то отображения из множества Ф  превращаются в подстановки степени три, а именно:
превращаются в подстановки степени три, а именно:
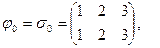
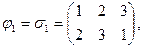
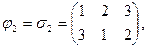
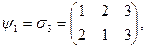
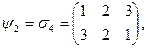
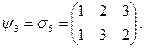
Эти подстановки составляют группу 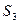 с такой же таблицей Кэли, что и для Ф
с такой же таблицей Кэли, что и для Ф 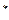 . Нетрудно понять, что здесь представлено изоморфное описание группы симметрий правильного треугольника.
. Нетрудно понять, что здесь представлено изоморфное описание группы симметрий правильного треугольника.
Пример 14.2. Группа симметрий прямоугольника изоморфна мультипликативной группе классов вычетов по 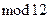 , взаимно простых с модулем, что тоже легко усмотреть из соответствующих таблиц Кэли.
, взаимно простых с модулем, что тоже легко усмотреть из соответствующих таблиц Кэли.
Пример 14.3. Легко увидеть, что 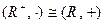 . Здесь отображение
. Здесь отображение 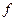 есть ни что иное, как
есть ни что иное, как 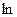 . Действительно, для любых
. Действительно, для любых 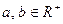
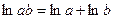 , притом, что отображение
, притом, что отображение 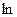 , очевидно, является биективным.
, очевидно, является биективным.
Пример 14.4. Группа вращений правильного треугольника вокруг его центра, представленная множеством Ф, изоморфна группе корней третьей степени из единицы.
Для конечных групп справедлива следующая теорема.
Теорема 14.1 (Кэли).
Каждая конечная группа порядка 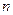 изоморфна некоторой подгруппе группы
изоморфна некоторой подгруппе группы 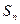 .
.
Доказательство. Пусть задана мультипликативная группа 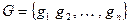 . Рассмотрим множество
. Рассмотрим множество 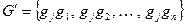 , где
, где 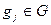 , а
, а 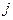 – любое фиксированное,
– любое фиксированное, 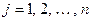 . Очевидно, что
. Очевидно, что 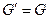 . Ибо элементы
. Ибо элементы 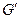 попарно различны и их ровно
попарно различны и их ровно 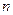 . Построим отображение
. Построим отображение 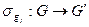 по правилу
по правилу 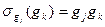 . Ясно, что такое отображение является биекцией. Рассмотрим теперь множество таких отображений
. Ясно, что такое отображение является биекцией. Рассмотрим теперь множество таких отображений 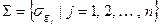 . Определим на множестве
. Определим на множестве 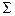 бинарную алгебраическую операцию. Именно:
бинарную алгебраическую операцию. Именно: 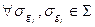
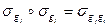 . Относительно этой операции множество
. Относительно этой операции множество 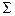 образует группу порядка
образует группу порядка 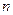 . Действительно, операция ассоциативна, ибо
. Действительно, операция ассоциативна, ибо
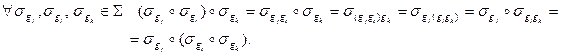
Роль единицы играет тождественное отображение  , так как
, так как 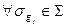 выполняется равенство
выполняется равенство 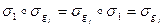 . Наконец, для каждого отображения
. Наконец, для каждого отображения 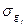 существует обратное отображение
существует обратное отображение 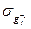 . Действительно, например,
. Действительно, например, 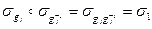 .
.
Зададим теперь отображение 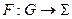 по правилу
по правилу  ,
, 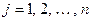 . Очевидно, что это биекция. Проверим выполнимость условия согласования операций. Имеем
. Очевидно, что это биекция. Проверим выполнимость условия согласования операций. Имеем
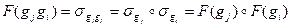 .
.
Так что отображение 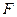 есть изоморфизм между
есть изоморфизм между  и
и 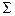 . Но
. Но 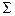 легко интерпретировать как группу
легко интерпретировать как группу 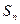 (тоже через изоморфизм):
(тоже через изоморфизм):
 ,
,
здесь 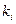 отвечает элементу
отвечает элементу 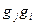 ,
, 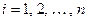 . Теорема доказана.
. Теорема доказана.
Таким образом, все конечные группы из указанных выше примеров можно отыскать в соответствующей симметрической группе. А, учитывая результат леммы 14.1, можно говорить о разбиении всех групп на попарно непересекающиеся классы изоморфных между собой, что приводит к возможности изучения групп «с точностью до изоморфизма».
Определение 14.2. Пусть  – группа и
– группа и 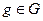 . Наименьшее натуральное число
. Наименьшее натуральное число 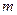 такое, что
такое, что 
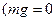 – в аддитивной записи), если оно существует, называется порядком элемента
– в аддитивной записи), если оно существует, называется порядком элемента 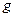 . В противном случае элемент
. В противном случае элемент 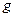 называют элементом бесконечного порядка. Обозначать будем
называют элементом бесконечного порядка. Обозначать будем 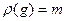 .
.
Если речь идет об элементах конечного порядка, сформулируем несколько свойств порядка элементов группы. Именно:
1. 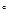
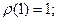
2. 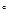
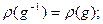
3. 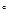
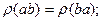
4. 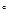 если
если 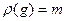 , то элементы
, то элементы 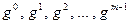 попарно различны;
попарно различны;
5. 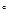 если
если 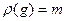 , то
, то 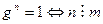 ;
;
6. 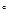 если
если  ,
, 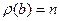 ,
, 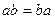 ,
,  , то
, то 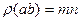 ;
;
7. 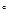 если
если  ,
, 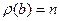 ,
, 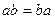 и
и  , то
, то 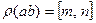 ;
;
8. 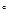 если
если 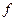 – изоморфизм, то
– изоморфизм, то 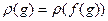 ;
;
9. 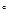 если
если 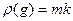 , то
, то 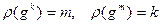 .
.
Легко видеть, что понятие показателя по заданному модулю в группе 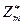 есть частный случай порядка элемента этой группы. Поэтому доказательства части свойств показателя можно перенести на общий случай, правда, учитывая возможную некоммутативность групповой операции.
есть частный случай порядка элемента этой группы. Поэтому доказательства части свойств показателя можно перенести на общий случай, правда, учитывая возможную некоммутативность групповой операции.
Докажем, например, свойство 7 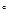 . Пусть
. Пусть 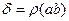 . Во-первых, легко устанавливаем, что число
. Во-первых, легко устанавливаем, что число 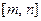 может служить порядком элемента
может служить порядком элемента 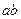 , ибо
, ибо
 .
.
Во-вторых, имеем
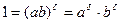 .
.
Здесь воспользовались перестановочностью элементов 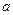 и
и 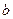 . Условие
. Условие  означает, множества, порождаемые степенями элементов
означает, множества, порождаемые степенями элементов 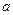 и
и 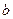 пересекаются лишь по единичному элементу, т.е.,
пересекаются лишь по единичному элементу, т.е., 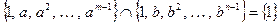 . Тогда получим, что
. Тогда получим, что 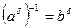 , откуда находим, что
, откуда находим, что  , т.е.,
, т.е., 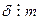 и
и 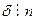 , а значит,
, а значит,  . А тогда
. А тогда  . Учитывая определение порядка, получаем, что
. Учитывая определение порядка, получаем, что 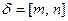 .
.
Доказательство остальных свойств оставим студентам.
Рассмотрим несколько примеров вычисления порядков элементов.
Пример 14.5. Для группы 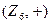 получаем:
получаем:
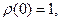
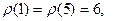
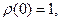
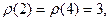
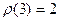 .
.
Пример 14.6. Для группы 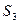 имеем:
имеем:

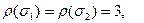
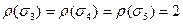 .
.
Ясно, что в конечных группах все элементы имеют конечный порядок, и эти порядки могут быть велики. Остановимся специально на случае группы 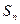 . но сначала несколько определений.
. но сначала несколько определений.
Определение 14.3. Подстановку  называют циклической или циклом, если множество реально перемещаемых символов в ней можно расположить один за другим так, что каждый из них переходит в следующий за ним, а последний переходит в первый.
называют циклической или циклом, если множество реально перемещаемых символов в ней можно расположить один за другим так, что каждый из них переходит в следующий за ним, а последний переходит в первый.
Пример 14.7. 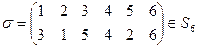 . Возможна запись
. Возможна запись 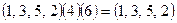 .
.
Определение 14.4. Количество реально перемещаемых символов в цикле называется его длиной.
В последнем примере длина цикла равна четырем, если отбросить циклы единичной длины. Нетрудно заметить, что справедлива следующая
Лемма 14.2. Порядок циклической подстановки равен ее длине.
Доказательство тривиальное.
А также справедлива
Лемма 14.3. Каждую подстановку можно разложить в произведение независимых циклов (т.е. множества реально перемещаемых символов которых попарно не пересекаются).
Доказательство тривиальное.
Учитывая последний результат, можно сформулировать теорему:
Теорема 14.2 (о порядке подстановки) .
Порядок подстановки равен наименьшему общему кратному длин независимых циклов, на которые она разлагается.
Доказательство. Если подстановку разложить в произведение независимых циклов, то, учитывая лемму 14.2 и свойство порядка 7 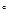 , сразу получаем результат теоремы.
, сразу получаем результат теоремы.
Пример 14.8. Пусть задана подстановка
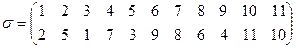
Найдем ее порядок, разложив на независимые циклы.
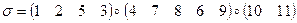 .
.
Тогда  .
.
Задача. 14.1. Построить подстановку наибольшего порядка степени 16.
Циклические группы.
Понятие циклической группы появилось в первой главе (см. опр. 1.24). Его появление было обусловлено необходимостью описания группы корней 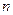 -й степени из единицы. Здесь будут даны некоторые дополнительные сведения. Тем не менее, повторим определение.
-й степени из единицы. Здесь будут даны некоторые дополнительные сведения. Тем не менее, повторим определение.
Определение 14.5. Группа  , в которой существует элемент
, в которой существует элемент 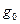 такой, что для любого
такой, что для любого 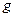
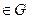 существует целое
существует целое 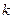 , что
, что 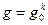 , называется циклической. При этом элемент
, называется циклической. При этом элемент 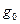 называется образующим элементом группы
называется образующим элементом группы  (в аддитивной записи
(в аддитивной записи 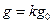 ).
).
Введем обозначение: через 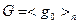 обозначаем циклические группы порядка
обозначаем циклические группы порядка 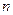 .
.
Пример 14.9 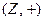 . Это бесконечная группа, где образующими элементами служат числа 1 и -1.
. Это бесконечная группа, где образующими элементами служат числа 1 и -1.
Пример 14.10. 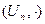 . Конечная группа порядка
. Конечная группа порядка 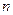 корней
корней 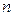 -ой степени из единицы. Образующими элементами в ней служат первообразные корни
-ой степени из единицы. Образующими элементами в ней служат первообразные корни 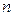 -ой степени.
-ой степени.
Пример 14.11.  . Циклическая группа третьего порядка, которую можно изоморфно представить в виде
. Циклическая группа третьего порядка, которую можно изоморфно представить в виде
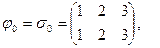
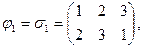
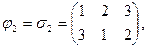
Циклические группы достаточно просто устроены, поэтому их описание несложно получить. Рассмотрим некоторые свойства циклических групп.
Теорема 14.3.
Конечные циклические группы одного порядка изоморфны между собой. Все бесконечные циклические группы изоморфны между собой.
Доказательство. Для доказательства конечного случая воспользуемся примером 14.10. Пусть 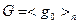 . Построим отображение
. Построим отображение 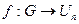 по правилу
по правилу 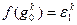 . Такое отображение, очевидно, является биекцией. Но при этом операции в группах согласованы. Именно:
. Такое отображение, очевидно, является биекцией. Но при этом операции в группах согласованы. Именно:
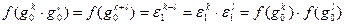 .
.
Для доказательства в бесконечном случае возьмем группу 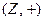 . Пусть
. Пусть  – бесконечная циклическая группа с порождающим элементом
– бесконечная циклическая группа с порождающим элементом 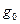 , т.е.,
, т.е., 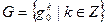 . Построим отображение
. Построим отображение 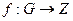 по правилу
по правилу 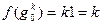 . Вновь видим, что отображение является биекцией. И
. Вновь видим, что отображение является биекцией. И
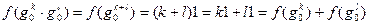 .
.
Так что в обоих случаях существует изоморфизм. Теорема доказана.
Эта теорема, в частности, говорит о том, что в качестве образца бесконечной циклической группы всегда можно взять группу 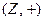 , а качестве представителя циклической группы порядка
, а качестве представителя циклической группы порядка 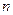 –
– 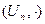 .
.
Рассмотрим свойства конечных циклических групп.
Лемма 14.4. Пусть 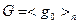 . Тогда
. Тогда 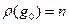 . Обратно, элемент порядка
. Обратно, элемент порядка 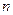 порождает циклическую группу порядка
порождает циклическую группу порядка 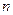 .
.
Доказательство. Действительно, в соответствии с теоремой 1.6 из первой главы 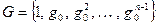 . Тогда
. Тогда 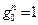 , ибо если
, ибо если 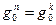 , где
, где 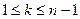 , то
, то 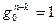 и, следовательно,
и, следовательно, 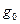 не порождает всю группу из
не порождает всю группу из 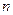 элементов, так как
элементов, так как 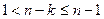 . Вторая часть леммы тривиальна.
. Вторая часть леммы тривиальна.
Лемма 14.5. Пусть 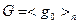 . Тогда
. Тогда 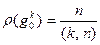 .
.
Доказательство. Во-первых, число 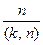 может быть порядком элемента
может быть порядком элемента 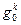 . Ибо если
. Ибо если 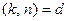 , то
, то  и
и 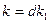 , при этом
, при этом 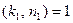 Тогда
Тогда 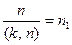 . Поэтому
. Поэтому
 .
.
Во-вторых, если 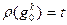 , то
, то 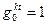 , откуда в силу свойства 5
, откуда в силу свойства 5 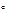 порядка элемента
порядка элемента 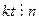 ,
,
значит, 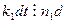 . И тогда
. И тогда 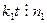 , но
, но 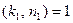 . Поэтому
. Поэтому 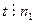 , т.е.,
, т.е., 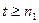 , а значит
, а значит 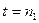 . Лемма доказана.
. Лемма доказана.
Лемма 14.6. Пусть 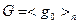 . Тогда для любого
. Тогда для любого  существует единственная подгруппа
существует единственная подгруппа  в
в  , порядок которой равен
, порядок которой равен 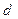 .
.
Доказательство. Пусть  , откуда
, откуда  . Тогда группу
. Тогда группу  можно представить как порожденную элементом
можно представить как порожденную элементом  , т.е.,
, т.е., 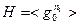 , так как
, так как 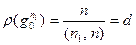 . Пусть теперь
. Пусть теперь 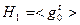 , где
, где  . Отсюда находим, что
. Отсюда находим, что  , а тогда по свойству 5
, а тогда по свойству 5 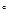 порядка
порядка 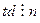 , т.е.,
, т.е., 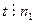 , например,
, например,  . Тогда для произвольного элемента
. Тогда для произвольного элемента  имеем
имеем
 ,
,
значит,  и тогда
и тогда 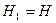 . Лемма доказана.
. Лемма доказана.
Лемма 14.7. Пусть 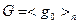 и
и  . Тогда в
. Тогда в  существует ровно
существует ровно 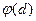 элементов порядка
элементов порядка 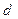 . Значит, в группе
. Значит, в группе  имеется
имеется  образующих элементов.
образующих элементов.
Доказательство. Пусть  . Элемент группы
. Элемент группы 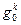 должен иметь порядок
должен иметь порядок 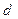 при
при 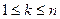 . Таким образом, должно быть
. Таким образом, должно быть 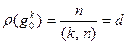 . Итак,
. Итак,
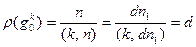 .
.
Значит, 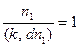 , т.е.,
, т.е., 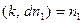 , откуда
, откуда 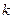 должно делиться на
должно делиться на 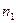 . Следовательно,
. Следовательно, 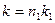 , где
, где 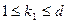 . И, наконец, сокращая на
. И, наконец, сокращая на 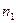 , получаем, что
, получаем, что 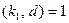 . Это означает, что подходят только те показатели
. Это означает, что подходят только те показатели 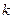 , для которых
, для которых 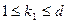 и
и 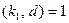 . Но таких, по определению функции Эйлера, как раз
. Но таких, по определению функции Эйлера, как раз 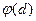 . Вторая часть леммы есть следствие первой.
. Вторая часть леммы есть следствие первой.
Полученные несложные результаты говорят о тесной связи понятий порядка элемента и циклической группы. В любой группе элемент конечного или бесконечного порядка порождает соответственно конечную циклическую группу заданного порядка или бесконечную циклическую группу.
Смежные классы. Теорема Лагранжа. Нормальные подгруппы. Факторгруппа.
Определение 14.6.Пусть  – группа,
– группа,  – подгруппа в
– подгруппа в  и
и 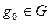 – произвольный элемент. Тогда левым смежным классом группы
– произвольный элемент. Тогда левым смежным классом группы  по подгруппе
по подгруппе  , порожденным элементом
, порожденным элементом 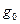 , называется множество
, называется множество  . Аналогично определяется соответствующий правый смежный класс
. Аналогично определяется соответствующий правый смежный класс 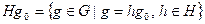 .
.
Лемма 14.8. Элемент 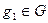 принадлежит классу
принадлежит классу 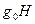 тогда и только тогда, когда
тогда и только тогда, когда 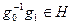 .
.
Доказательство. Тривиальное.
Лемма 14.9. Бинарное отношение  на множестве
на множестве  , определяемое соотношением
, определяемое соотношением 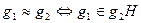 есть отношение эквивалентности.
есть отношение эквивалентности.
Доказательство. Рефлексивность и симметричность практически очевидны. Докажем транзитивность отношения. Пусть 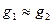 и
и 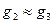 , тогда
, тогда 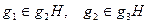 . Таким образом,
. Таким образом, 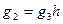 для некоторого
для некоторого 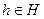 , а
, а 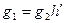 для некоторого
для некоторого 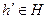 . Делая подстановку, получаем
. Делая подстановку, получаем
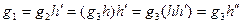 для
для 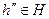 .
.
Но это и означает, что 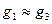 .
.
Легко видеть, что левые смежные классы  по
по  есть те попарно непересекающиеся классы, на которые разбивается множество
есть те попарно непересекающиеся классы, на которые разбивается множество  данным отношением эквивалентности.
данным отношением эквивалентности.
Лемма 14.10. Смежные классы группы  по подгруппе
по подгруппе  равномощны.
равномощны.
Доказательство. Это легко усматривается из естественной биекции 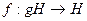 , где
, где 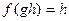 . Здесь
. Здесь  – тоже смежный класс, порождаемый единицей группы.
– тоже смежный класс, порождаемый единицей группы.
Теорема 14.4.
Множества левых и правых смежных классов по данной подгруппе равномощны.
Доказательство. Следует из того, что 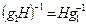 и
и 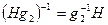 . Здесь
. Здесь 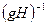 – совокупность элементов группы, обратных элементам данного класса. Таким образом, имеется взаимно однозначное соответствие между множествами левых и правых смежных классов группы
– совокупность элементов группы, обратных элементам данного класса. Таким образом, имеется взаимно однозначное соответствие между множествами левых и правых смежных классов группы  по подгруппе
по подгруппе  .
.
Определение 14.7. Кардинальное число левых (правых) смежных классов группы  по подгруппе
по подгруппе  называется индексом группы
называется индексом группы  по подгруппе
по подгруппе  и обозначается
и обозначается 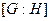 .
.
Таким образом, фактормножество 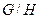 имеет мощность
имеет мощность 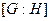 . В случае, когда группа
. В случае, когда группа  конечна, индекс любой ее подгруппы конечен, и имеет место следующая
конечна, индекс любой ее подгруппы конечен, и имеет место следующая
Теорема 14.5 (Лагранжа).
Если  – конечная группа, то для любой ее подгруппы
– конечная группа, то для любой ее подгруппы  справедливо соотношение
справедливо соотношение 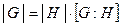 .
.
Доказательство. Так как классы равномощны и попарно не пересекаются, то число элементов группы равно числу элементов одного класса 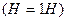 , умноженное на количество классов.
, умноженное на количество классов.
Следствие 1. Порядок любого элемента конечной группы является делителем порядка группы.
Доказательство. Элементы конечного порядка порождают конечные циклические подгруппы.
Следствие 2. Конечная группа простого порядка – циклична.
Доказательство. Любой неединичный элемент такой группы порождает циклическую подгруппу, порядок которой должен делить порядок группы. А последний есть простое число. Следовательно, порядок подгруппы совпадает с порядком группы.
Следствие 3. В конечной группе простого порядка все неединичные элементы являются образующими.
Доказательство. Тривиально.
Пример 14.12. 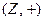 ,
, 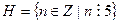 . Очевидно, что классами смежности здесь служат классы вычетов по модулю 5. Именно:
. Очевидно, что классами смежности здесь служат классы вычетов по модулю 5. Именно: 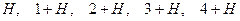 . Значит,
. Значит, 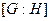 = 5.
= 5.
Пример 14.13. 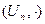 ,
,  для
для 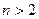 . Ясно, что число
. Ясно, что число 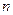 должно быть четным, например,
должно быть четным, например, 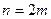 . Тогда получим в соответствии с теоремой Лагранжа
. Тогда получим в соответствии с теоремой Лагранжа 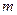 классов вида
классов вида 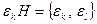 , где
, где  .
.
Пример 14.14. 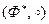 ,
, 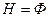 . Здесь, как легко видеть, будет всего два класса, причем класс, отличный от подгруппы
. Здесь, как легко видеть, будет всего два класса, причем класс, отличный от подгруппы  , составляют отображения, описывающие осевые симметрии
, составляют отображения, описывающие осевые симметрии 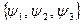 . Например,
. Например,
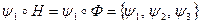 .
.
Пример 14.15. 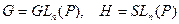 . Учитывая лемму 14.8, легко находим, что классы смежности образуют матрицы из
. Учитывая лемму 14.8, легко находим, что классы смежности образуют матрицы из 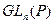 , имеющие одинаковые определители.
, имеющие одинаковые определители.
Пример 14.16.  . В этом случае класс составляют многочлены с одинаковыми свободными членами.
. В этом случае класс составляют многочлены с одинаковыми свободными членами.
Определение 14.8. Подгруппа  группы
группы  называется нормальной, или инвариантной, или нормальным делителем, если для любого элемента
называется нормальной, или инвариантной, или нормальным делителем, если для любого элемента 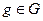 выполнено
выполнено 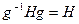 . Обозначение:
. Обозначение: 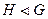 .
.
Ясно, что это понятие приобретает смысл для неабелевых групп. Отметим два критерия нормальности.
Теорема 14.6.
Подгруппа  группы
группы  является нормальной тогда и только тогда, когда
является нормальной тогда и только тогда, когда 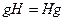 для любого
для любого 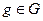 .
.
Доказательство. Тривиально.
Следствие. Любая подгруппа индекса 2 нормальна.
Теорема 14.7.
Подгруппа  группы
группы  является нормальной тогда и только тогда, когда
является нормальной тогда и только тогда, когда 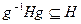 для любого
для любого 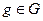 .
.
Доказательство. Необходимость очевидна.
Достаточность. Если 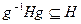 и
и 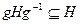 , то
, то
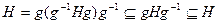 ,
,
откуда 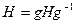 и, аналогично,
и, аналогично, 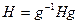 .
.
Пример 14.17. Подгруппа 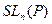 нормальна в
нормальна в 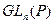 , что легко проверяется при помощи второго критерия, учитывая теорему об умножении определителей.
, что легко проверяется при помощи второго критерия, учитывая теорему об умножении определителей.
Пример 14.18. Знакопеременная группа 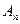 четных подстановок степени
четных подстановок степени 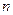 нормальна в симметрической группе
нормальна в симметрической группе 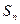 как подгруппа индекса 2.
как подгруппа индекса 2.
Пример 14.19. Аналогично можно утверждать, что Ф нормальна в 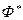 .
.
Определение 14.9. Пусть  – нормальная подгруппа в
– нормальная подгруппа в  . На фактормножестве
. На фактормножестве 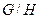 определим операцию умножения (сложения в аддитивном случае) классов соотношением:
определим операцию умножения (сложения в аддитивном случае) классов соотношением:
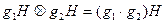 (
( 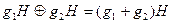 ).
).
Это определение задает на 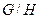 бинарную алгебраическую операцию. Нормальность
бинарную алгебраическую операцию. Нормальность  определяет корректность операции, т.е., независимость результата от выбора представителя класса. Действительно, пусть
определяет корректность операции, т.е., независимость результата от выбора представителя класса. Действительно, пусть 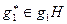 и
и 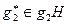 . Тогда
. Тогда 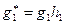 , а
, а  для некоторых
для некоторых  . Имеем
. Имеем
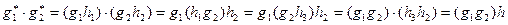 .
.
Таким образом, 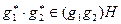 . Значит,
. Значит,
 .
.
Лемма 14.11. Фактормножество 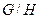 относительно операции умножения (сложения) классов образует группу, называемую факторгруппой группы
относительно операции умножения (сложения) классов образует группу, называемую факторгруппой группы  по подгруппе
по подгруппе  .
.
Доказательство. Следует проверить выполнимость аксиом. Во-первых, операция ассоциативна. Действительно, для любых 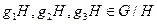 имеем
имеем
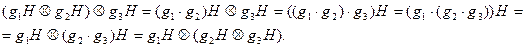
Нейтральным элементом является класс 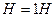 , что моментально проверяется. А для каждого
, что моментально проверяется. А для каждого 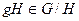 обратным будет класс
обратным будет класс 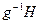 , ибо
, ибо
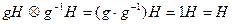 ,
,
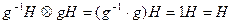 .
.
Лемма доказана.
Пример 14.20. Пусть задана группа 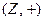 ,
, 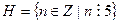 . В этом примере множество
. В этом примере множество 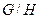 есть группа классов вычетов по модулю 5 относительно операции сложения по
есть группа классов вычетов по модулю 5 относительно операции сложения по
модулю 5, т.е. 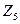 .
.
Пример 14.21. Пусть задана группа 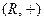 и подгруппа в ней
и подгруппа в ней 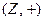 . Два вещественных числа попадают в один класс тогда и только тогда, когда имеют одинаковую дробную часть. Таким образом, сложение классов происходит по правилу:
. Два вещественных числа попадают в один класс тогда и только тогда, когда имеют одинаковую дробную часть. Таким образом, сложение классов происходит по правилу:
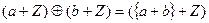 , где
, где 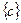 означает дробную часть с.
означает дробную часть с.
Пример 14.22. Пусть 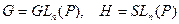 . Классы обсуждались в примере 14.15, а нормальность подгруппы
. Классы обсуждались в примере 14.15, а нормальность подгруппы  в примере 14.17. Результат умножения классов есть класс, содержащий матрицы, определитель которых равен произведению определителей матриц, входящих в классы-сомножители.
в примере 14.17. Результат умножения классов есть класс, содержащий матрицы, определитель которых равен произведению определителей матриц, входящих в классы-сомножители.
В примере 14.20 порядок факторгруппы равен 5, а в следующих примерах имеем факторгруппы бесконечного порядка.
Лемма 14.12. Факторгруппа циклической группы по любой ее подгруппе сама циклична.
Доказательство. Самостоятельно.
Гомоморфизм групп
Определение 14.10. Пусть 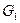 и
и 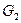 – группы (используем мультипликативную запись). Тогда отображение
– группы (используем мультипликативную запись). Тогда отображение 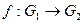 называется гомоморфизмом групп, если для любых
называется гомоморфизмом групп, если для любых 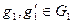
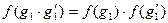 .
.
Легко видеть, что взаимно однозначный гомоморфизм есть изоморфизм групп. Отметим некоторые свойства гомоморфизма.
1. 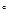
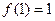 ;
;
2. 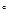
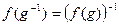 ;
;
3. 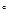 Гомоморфный образ группы есть группа.
Гомоморфный образ группы есть группа.
Докажем последнее утверждение. Воспользуемся критерием подгруппы (см. т. 1.5). Пусть 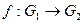 – гомоморфизм и
– гомоморфизм и 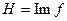 . Тогда для любых
. Тогда для любых 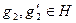 имеем для некоторых
имеем для некоторых 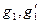 таких, что
таких, что  и
и 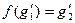 , что
, что
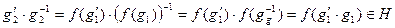 .
.
Как следует из первого свойства, гомоморфный образ единицы есть единица. Но возможно существуют и другие элементы, отображающиеся в единицу. Отсюда
Определение 14.11. .Гомоморфный образ единицы группы при гомоморфизме 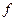 называется ядром гомоморфизма и обозначается
называется ядром гомоморфизма и обозначается 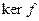 .
.
Лемма 14.13. Пусть 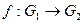 – гомоморфизм. Тогда
– гомоморфизм. Тогда 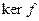 подгруппа в
подгруппа в 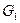 .
.
Доказательство. По критерию подгруппы (т. 1.5) для любых 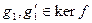 должно выполняться включение
должно выполняться включение 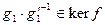 . Действительно,
. Действительно,
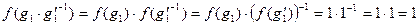 .
.
Следовательно, 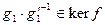 и
и 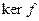 подгруппа в
подгруппа в 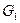 . Лемма доказана.
. Лемма доказана.
Теорема 14.8 (первая теорема о гомоморфизмах групп).
Пусть 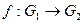 – гомоморфизм групп и
– гомоморфизм групп и  . Тогда
. Тогда 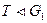 и два элемента из
и два элемента из 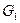 имеют один и тот же образ в
имеют один и тот же образ в 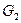 тогда и только тогда, когда лежат в одном классе смежности по подгруппе
тогда и только тогда, когда лежат в одном классе смежности по подгруппе 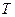 .
.
Доказательство. По лемме 14.13 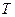 – подгруппа в
– подгруппа в 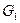 . Для доказательства нормальности воспользуемся теоремой 14.7. Имеем для произвольных
. Для доказательства нормальности воспользуемся теоремой 14.7. Имеем для произвольных 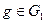 и
и 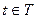 :
:
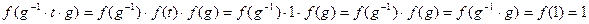 .
.
Значит, 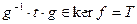 . И тогда
. И тогда  , т.е.,
, т.е., 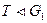 .
.
Вторая часть теоремы. Достаточность. Пусть 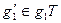 , тогда
, тогда 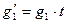 для некоторого
для некоторого 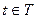 . Отсюда находим, что
. Отсюда находим, что
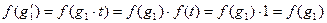 .
.
Необходимость. Если  , то
, то 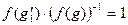 . Тогда отсюда получим, что
. Тогда отсюда получим, что 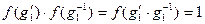 , а значит,
, а значит, 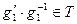 . А тогда указанные элементы лежат в одном классе по подгруппе
. А тогда указанные элементы лежат в одном классе по подгруппе 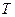 по лемме 14.8. Теорема доказана.
по лемме 14.8. Теорема доказана.
Теорема 14.9 (вторая теорема о гомоморфизмах групп).
Пусть  – группа,
– группа,  ,
, 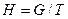 . Тогда существует гомоморфизм
. Тогда существует гомоморфизм  на
на  с ядром
с ядром 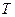 . Его называют естественным.
. Его называют естественным.
Доказательство. Построим отображение 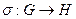 по правилу: для любого
по правилу: для любого 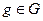
 . Проверим условие согласования операций. Для любых
. Проверим условие согласования операций. Для любых 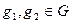
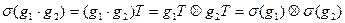 .
.
Значит,  – гомоморфизм. Так как
– гомоморфизм. Так как 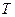 есть единица в
есть единица в  , то совокупность элементов
, то совокупность элементов 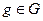 , отображаемых в
, отображаемых в 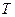 должна совпадать с классом
должна совпадать с классом 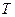 , ибо
, ибо 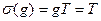 , т.е.,
, т.е.,  . Откуда ясно, что
. Откуда ясно, что 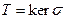 . Теорема доказана.
. Теорема доказана.
Теорема 14.10 (третья теорема о гомоморфизмах групп).
Если 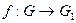 – гомоморфизм и
– гомоморфизм и  , то группы
, то группы 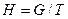 и
и 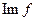 – изоморфны.
– изоморфны.
Доказательство. Построим отображение 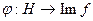 по следующему правилу: для любого класса
по следующему правилу: для любого класса 
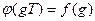 . Так как элементы группы
. Так как элементы группы  , имеющие общий образ в
, имеющие общий образ в 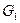 , лежат в одном классе смежности по ядру
, лежат в одном классе смежности по ядру 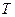 , то отображение
, то отображение 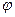 инъективно. Оно же очевидно и сюръективно. Остается проверить условие согласования операций. Именно: для любых
инъективно. Оно же очевидно и сюръективно. Остается проверить условие согласования операций. Именно: для любых 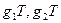 имеем
имеем
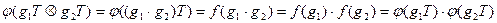 .
.
Теорема доказана. Теоремы 14.9 и 14.10 можно проиллюстрировать такой диаграммой:
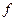



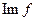


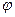

Итак, подытоживая, можно сказать, что ядро любого гомоморфизма есть нормальная подгруппа, а любая нормальная подгруппа является ядром некоторого гомоморфизма, образ которого изоморфен факторгруппе данной группы по нормальному делителю.
| <== предыдущая лекция | | | следующая лекция ==> |
| | | Этнокультурное образование: сущность, функции, понятия и социальный аспект |
Дата добавления: 2019-07-26; просмотров: 3083;
