АРИФМЕТИКА. Теория делимости 6 страница
Лемма 13.31. Если число 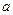 принадлежит показателю
принадлежит показателю 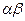 по модулю
по модулю  , то число
, то число 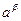 принадлежит показателю
принадлежит показателю 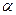 по модулю
по модулю  .
.
Доказательство. Во-первых, 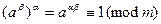 . С другой стороны, если бы для некоторого
. С другой стороны, если бы для некоторого 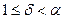
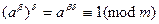 , то, так как
, то, так как 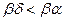 , то противоречило бы понятию показателя
, то противоречило бы понятию показателя 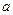 по модулю
по модулю  .
.
Лемма 13.32. Если 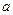 принадлежит показателю
принадлежит показателю 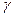 , а
, а 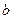 принадлежит показателю
принадлежит показателю 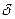 по модулю
по модулю  и
и 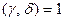 , то число
, то число 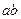 принадлежит показателю
принадлежит показателю 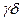 .
.
Доказательство. С одной стороны,
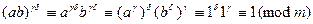 .
.
Это говорит о том, что число 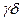 может служить показателем данного произведения. С другой стороны, если
может служить показателем данного произведения. С другой стороны, если 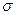 является показателем указанного произведения модулю
является показателем указанного произведения модулю  , то
, то 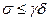 . Кроме того, имеем
. Кроме того, имеем
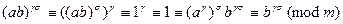 .
.
Тогда по следствию из леммы 13.30 получим, что  , но
, но 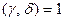 . Поэтому
. Поэтому  .
.
Аналогично,
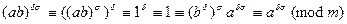 .
.
Значит, 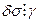 , но
, но 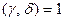 , поэтому
, поэтому 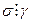 . И вновь в силу взаимной простоты
. И вновь в силу взаимной простоты 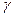 и
и 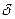 находим, что
находим, что 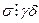 , т.е.,
, т.е., 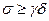 . А тогда
. А тогда 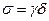 .
.
Теорема 13. 18. Существуют первообразные корни по простому модулю  .
.
Доказательство. Пусть 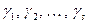 будут все различные показатели, которым принадлежат числа
будут все различные показатели, которым принадлежат числа 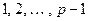 по модулю
по модулю  . Обозначим через
. Обозначим через  – НОК указанных чисел. Пусть
– НОК указанных чисел. Пусть 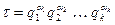 . Каждый множитель последнего разложения
. Каждый множитель последнего разложения 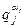 ,
, 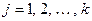 , делит по крайней мере одно число
, делит по крайней мере одно число 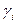 ,
, 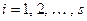 , которое, следовательно, можно представить в виде
, которое, следовательно, можно представить в виде 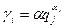 . Пусть
. Пусть 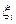 будет одним из чисел ряда
будет одним из чисел ряда 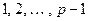 , принадлежащих показателю
, принадлежащих показателю 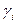 . Тогда число
. Тогда число 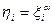 принадлежит показателю
принадлежит показателю 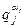 по лемме 13.31. А в соответствии с леммой 13.32 произведение
по лемме 13.31. А в соответствии с леммой 13.32 произведение 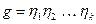 принадлежит показателю
принадлежит показателю 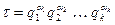 . Отсюда заключаем, что число
. Отсюда заключаем, что число 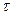 является делителем
является делителем 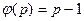 . Но поскольку все числа
. Но поскольку все числа 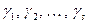 делят
делят 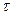 , то все числа ряда
, то все числа ряда 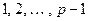 являются решениями сравнения
являются решениями сравнения 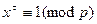 . Поэтому по лемме 13.13 количество таких решений
. Поэтому по лемме 13.13 количество таких решений  . Следовательно,
. Следовательно, 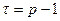 и тогда
и тогда 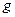 – первообразный корень по модулю
– первообразный корень по модулю  . Теорема доказана.
. Теорема доказана.
Теорема 13.19. Пусть 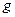 – первообразный корень по модулю
– первообразный корень по модулю  . Существует такое
. Существует такое 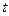 , что число
, что число 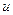 , определяемое равенством
, определяемое равенством 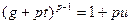 , не делится на
, не делится на  . Тогда
. Тогда 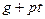 будет первообразным корнем по модулю
будет первообразным корнем по модулю 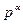 при любом
при любом 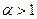 .
.
Доказательство. Действительно, имеем
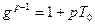 ,
,
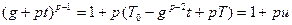 ,
,
где, одновременно с 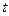 ,
, 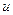 пробегает ПСВ по модулю
пробегает ПСВ по модулю  . Поэтому можно указать
. Поэтому можно указать 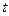 с условием, что
с условием, что 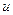 не делится на
не делится на  . При таком
. При таком 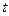 из последнего равенства выводим
из последнего равенства выводим
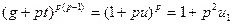 ,
,
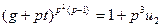 ,
,
. . . . . . . . . . . . . . .
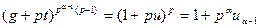 ,
,
где все 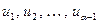 не делятся на
не делятся на  . Пусть
. Пусть 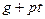 принадлежит показателю
принадлежит показателю 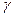 по модулю
по модулю 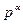 . Тогда имеем
. Тогда имеем
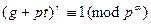 ,
,
Откуда, в частности, находим
 .
.
Поэтому по следствию 1 из леммы 13.30 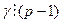 и по следствию 2 из той же леммы
и по следствию 2 из той же леммы 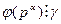 , т.е.,
, т.е., 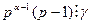 , поэтому
, поэтому 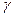 должно иметь вид
должно иметь вид 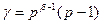 , где
, где 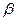 есть одно из чисел
есть одно из чисел 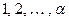 . А так как выше указанные равенства показывают, что
. А так как выше указанные равенства показывают, что
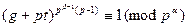
Верно при 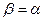 и неверно при
и неверно при 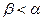 , то
, то 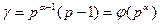 . Значит,
. Значит, 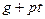 –
–
первообразный корень по модулю 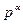 . Теорема доказана.
. Теорема доказана.
Теорема 13.20. Пусть 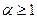 и
и 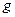 – первообразный корень по модулю
– первообразный корень по модулю 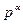 . Нечетное
. Нечетное 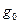 из чисел
из чисел 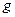 и
и 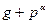 будет первообразным корнем по модулю
будет первообразным корнем по модулю 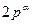 .
.
Доказательство. Действительно, 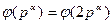 . Далее, сравнения
. Далее, сравнения
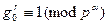 и
и 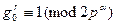
Могут выполняться лишь одновременно, так как 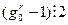 . А так как
. А так как 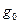 – первообразный корень по модулю
– первообразный корень по модулю 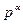 и первое сравнение верно при
и первое сравнение верно при 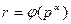 и неверно при
и неверно при 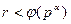 , то тем самым и второе сравнение верно при
, то тем самым и второе сравнение верно при 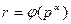 и неверно при
и неверно при 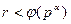 . Тогда
. Тогда 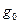 – первообразный корень по модулю
– первообразный корень по модулю 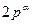 . Теорема доказана.
. Теорема доказана.
Для разыскания первообразных корней по модулям 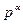 и
и 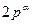 , где
, где  – простое нечетное и
– простое нечетное и 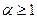 , можно воспользоваться следующим результатом.
, можно воспользоваться следующим результатом.
Теорема 13.21. Пусть 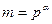 или
или  и
и 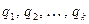 – все различные простые делители числа
– все различные простые делители числа 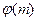 . Для того, чтобы число
. Для того, чтобы число 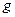 , взаимно простое с
, взаимно простое с  , было первообразным корнем по модулю
, было первообразным корнем по модулю  , необходимо и достаточно, чтобы это
, необходимо и достаточно, чтобы это 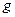 не удовлетворяло ни одному из сравнений
не удовлетворяло ни одному из сравнений
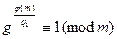 ,
, 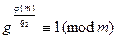 , . . . ,
, . . . ,  .
.
Доказательство. Необходимость. Если 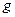 – первообразный корень по модулю
– первообразный корень по модулю  , то тем самым оно принадлежит показателю
, то тем самым оно принадлежит показателю 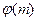 , и поэтому не может удовлетворять указанным выше сравнениям.
, и поэтому не может удовлетворять указанным выше сравнениям.
Достаточность. Пусть теперь 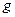 не удовлетворяет ни одному указанному сравнению. Если показатель
не удовлетворяет ни одному указанному сравнению. Если показатель 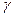 , которому принадлежит
, которому принадлежит 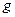 , меньше
, меньше 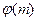 , то, обозначая один из простых делителей
, то, обозначая один из простых делителей 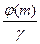 через
через 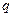 , имели бы
, имели бы 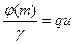 . Тогда
. Тогда 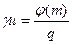 и
и 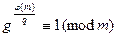 , что противоречит условию. Следовательно,
, что противоречит условию. Следовательно, 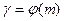 и
и 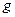 – первообразный корень по модулю
– первообразный корень по модулю  . Теорема доказана.
. Теорема доказана.
В следующей главе, исходя из общих теоретико-групповых соображений, будет указано количество первообразных корней по модулю  . Опуская результаты по модулю
. Опуская результаты по модулю 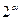 , заметим, что по всем прочим модулям первообразные корни не существуют.
, заметим, что по всем прочим модулям первообразные корни не существуют.
Пример 13. 27. Пусть требуется найти первообразный корень по модулю 43. Вычисляем 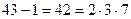 . Выберем в качестве предполагаемого первообразного корня число
. Выберем в качестве предполагаемого первообразного корня число 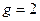 . Далее, проверяем выполнимость сравнений
. Далее, проверяем выполнимость сравнений
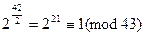 ,
, 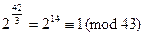 ,
, 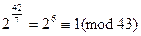 .
.
Первое и третье сравнения дают соответственно  и
и 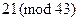 , а вот второе оказывается справедливым. Поэтому 2 не является первообразным корнем по модулю 43. Возьмем теперь число
, а вот второе оказывается справедливым. Поэтому 2 не является первообразным корнем по модулю 43. Возьмем теперь число 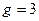 . Имеем
. Имеем
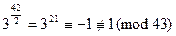 ,
, 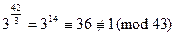 ,
, 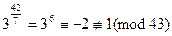 .
.
Ни одно из сравнений не выполняется, поэтому 3 – первообразный корень по модулю 43.
Вычислим теперь первообразный корень по модулю 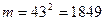 . Применим теорему 13.19. Имеем
. Применим теорему 13.19. Имеем
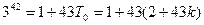 ,
,
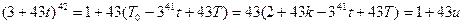 .
.
Теперь при  число
число 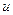 не делится на 43. Поэтому
не делится на 43. Поэтому 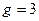 будет первообразным корнем по модулю 43.
будет первообразным корнем по модулю 43.
По модулю  тогда по теореме 13.20
тогда по теореме 13.20 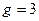 будет первообразным и по этому модулю.
будет первообразным и по этому модулю.
Вновь считаем, что 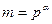 или
или  и
и 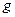 – первообразный корень по модулю
– первообразный корень по модулю  .
.
Лемма 13.33. Если 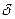 пробегает наименьшие неотрицательные вычеты по модулю
пробегает наименьшие неотрицательные вычеты по модулю 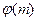 , то
, то  пробегает приведенную систему вычетов по модулю
пробегает приведенную систему вычетов по модулю  .
.
Доказательство. Простое следствие леммы 13.29.
Определение 13.23. Пусть число 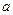 взаимно просто с
взаимно просто с  и
и 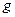 – первообразный корень по модулю
– первообразный корень по модулю  . Тогда, если
. Тогда, если
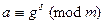 ,
,
где 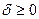 , число
, число 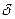 называется дискретным логарифмом числа
называется дискретным логарифмом числа 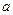 по основанию
по основанию 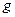 по модулю
по модулю  , или индексом и обозначается
, или индексом и обозначается 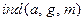 .
.
Ввиду леммы 13.33 каждое число 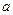 взаимно простое с
взаимно простое с  имеет единственный индекс среди чисел
имеет единственный индекс среди чисел 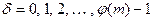 . Зная какой-либо индекс из указанного набора можно представить все дискретные логарифмы числа
. Зная какой-либо индекс из указанного набора можно представить все дискретные логарифмы числа 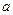 . Это будут все неотрицательные числа класса
. Это будут все неотрицательные числа класса  . А числа с данным индексом
. А числа с данным индексом 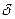 образуют класс чисел по модулю
образуют класс чисел по модулю  .
.
Лемма 13.34. Для 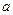 и
и 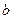 взаимно простых с
взаимно простых с 
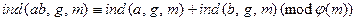 .
.
Доказательство. Имеем
 ,
, 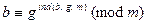 .
.
Перемножив почленно эти сравнения, получим
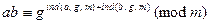 .
.
Значит, сумма в показателе последнего сравнения есть один из дискретных логарифмов произведения 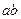 .
.
Следствие. 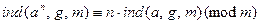 .
.
Ввиду практической пользы дискретных логарифмов имеются таблицы индексов для всех не очень больших  . Нахождение дискретных логарифмов для больших значений
. Нахождение дискретных логарифмов для больших значений  представляет собой сложную вычислительную задачу.
представляет собой сложную вычислительную задачу.
Дата добавления: 2019-07-26; просмотров: 303;
