ЛИНЕЙНЫЕ ОПЕРАТОРЫ В КОНЕЧНОМЕРНЫХ ПРОСТРАНСТВАХ 5 страница

Высота корневого вектора и кратность собственного значения естественно связаны неравенством 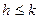. Введем еще понятие максимальной высоты корневых векторов.

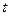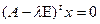Определение 9.24. Наименьшее натуральное такое, что для любого корневого вектора выполняется равенство , называется максимальной высотой корневых векторов.

Максимальная высота, очевидно, удовлетворяет неравенству 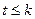, но не более того, ибо, например, для оператора простой структуры независимо от кратности собственного значения максимальная высота равна 1. Но .

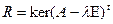Введем в обращение специальные подпространства: 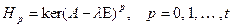. Эти множества будут подпространствами потому, что это ядра операторов. Тогда получим следующую цепочку включений в соответствии с леммой 9.18:

.

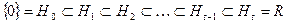Обозначим и будем теперь строить специальный базис в 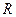. Пусть система векторов из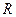 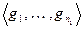является линейно независимой и ее линейная оболочка в прямой сумме с 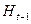задает , т.е.,

.

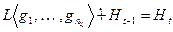Такая система заведомо существует, ибо 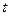– максимальная высота корневых векторов. Это значит, что никакая ненулевая линейная комбинация векторов 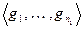не принадлежит 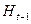. При этом 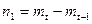. Построим следующую башню векторов:

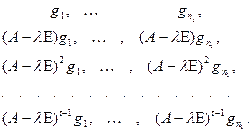
Ее верхний этаж образуют векторы высоты 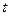, следующий – высоты 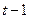и т.д. Самый нижний, первый, этаж занимают векторы высоты 1, т.е., собственные векторы. Легко можно доказать, что башня векторов линейно независима. Действительно, если записать линейную комбинацию векторов с неопределенными коэффициентами и приравнять ее нулю, то окажется, что это возможно лишь при нулевом наборе коэффициентов. Чтобы это увидеть, достаточно подействовать на обе части равенства оператором 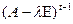. Тогда все слагаемые с первого по предпоследний этаж будут обнулены, а в последнем этаже получим

.

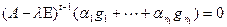Отсюда получаем, что

,

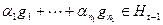что возможно лишь тогда, когда

,

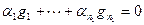и в силу линейной независимости системы 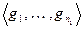получаем, что .

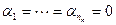Таким образом, в исходной линейной комбинации остаются векторы с первого по предпоследний этажи. Тогда на обе части ее подействуем оператором 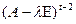и проведем похожее на предыдущее рассуждение, что влечет равенство нулю коэффициентов предпоследнего этажа. И т.д. Итак, считаем, что линейная независимость башни векторов обоснована.

Теперь припишем к векторам предпоследнего этажа систему 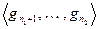, если она существует, такую, что линейная оболочка векторов предпоследнего этажа в прямой сумме с 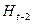задавала бы 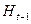, т.е., никакая ненулевая линейная комбинация векторов предпоследнего этажа не принадлежит 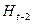. Далее, достроим новую башню, используя прежний принцип. Получим

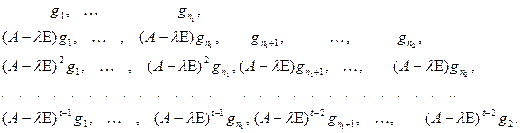
Здесь 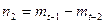. Полученное здание векторов тоже образует линейно независимую систему. Доказательство этого факта проводится так же, как описано выше. Если предпоследний этаж дополнить невозможно, то переходим на следующий под ним этаж. Продолжая этот процесс, наконец, подойдем к первому этажу. Возможно дополнение векторов нижнего этажа какой-то системой собственных векторов так, что линейная оболочка всего нижнего этажа равна , т.е., собственному подпространству, отвечающему собственному значению 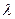. И 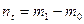. Вновь можно показать, что все здание векторов есть линейно независимая система.

Имеем равенства

,

.

. . . . . . .

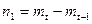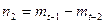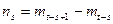(9.12)

. . . . . . . .

.

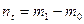Отсюда видно, что общая сумма векторов равна 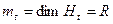. Таким образом, полученное здание векторов есть базис 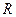. Упростим обозначения в этой системе.

Здесь в скобках над вектором указана его высота. Разобьем этот базис на части, которые являются столбцами в данном здании. Построим на таких столбцах линейные оболочки. Получим 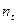подпространств, каждое из которых будет инвариантным относительно оператора 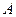. Действительно, если подействовать на векторы порождающей системы оператором 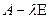, то будем получать либо вектор высоты на единицу меньшей, чем у исходного, либо нулевой вектор:

.

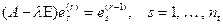Такие пространства назовем циклическими. Таким образом, доказана лемма

Лемма 9.22. Корневое подпространство разлагается в прямую сумму циклических подпространств:

.

Доказательство следует из теоремы 5.7.

В силу инвариантности циклических подпространств матрица оператора, индуцированного на 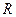оператором А в свою очередь может быть представлена в клеточно-диагональной форме. Рассмотрим вид соответствующих клеток на примере 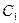, т.е., рассмотрим матрицу оператора, индуцированного на 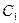. Имеем (при нумерации векторов, начиная снизу):

,

,

. . . . . . . . . . . . . . . . .

,

.

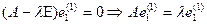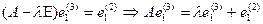
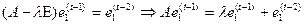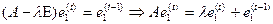Эти равенства дают следующую матрицу.

.

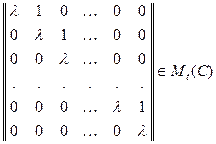Такая матрица-клетка называется клеткой, или ящиком, Жордана. Таким образом, матрицы индуцированных операторов на циклических подпространствах имеют вид клеток Жордана. Значит, всю матрицу оператора А можно собрать из клеток Жордана, если объединить корневые базисы указанного вида в один канонический корневой базис. При этом обычно придерживаются следующих правил. Во-первых, сначала выписываются клетки для одного собственного значения, затем все клетки для другого и т.д. Во-вторых, сначала выписываются клетки больших размеров, а за ними по убыванию – меньших для данного собственного значения. Возникающая матрица называется жордановой нормальной формой матрицы (оператора). В случае оператора простой структуры его жорданова матрица оказывается диагональной, ибо для каждого собственного значения существуют векторы с высотой не более 1. Итак, жорданова матрица (ЖНФ) имеет вид:

.

Итогом предыдущих рассуждений является теорема:

Теорема 9.18.

Для оператора действующего в комплексном пространстве существует канонический корневой базис, в котором его матрица имеет жорданову нормальную форму.

И, наконец,

Теорема 9.19 (второй критерий подобия матриц).

Две квадратные комплексные матрицы подобны тогда и только тогда, когда имеют одинаковые жордановы нормальные формы.

Доказательство. Несмотря на то, что матрицы существуют независимо от операторов, удобно привлекать операторные рассуждения к матричным проблемам. Поэтому следует рассматривать упомянутые матрицы как матрицы операторов.

Практическое построение жордановой нормальной формы матрицы

При получении такой задачи сразу становится ясным то, что требуется найти собственные значения матрицы (оператора). Кстати, саму матрицу можно рассматривать как оператор в пространстве столбцов. Таким образом, нужно построить характеристический многочлен и постараться найти его корни. Считая формально, что работаем в комплексном пространстве, утверждаем, что все корни суть собственные значения оператора. Далее, возникает вопрос определения размеров и количества жордановых клеток для данного собственного значения. Для этого введет величину 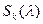означающую число жордановых клеток размерности 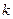для собственного значения 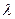. Легко видеть (глядя на схему корневого базиса), что размер клетки – это высота соответствующего столбца в базисе, т.е., размерность порождаемого им циклического подпространства. Тогда

,

,

,

. . . . . . . .

,

. . . . . . . . .

,

.

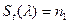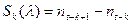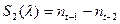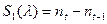Заменяя значения 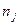, , 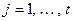на выражения (9.12), получим

,

,

,

. . . . . . . .

,

. . . . . . . . .

,

.

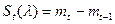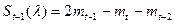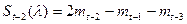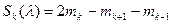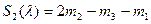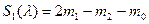Ясно, что общей формулой является следующая:

.

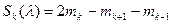где 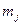– дефекты соответствующих операторов (матриц). Учитывая соотношение между рангом и дефектом 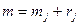, , 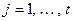и тот факт, что ранги считать проще, получаем формулу для 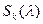, описывающую то же число посредством вычисленных рангов матриц (операторов). Именно:

.

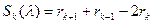Пример 9.25. Построить ЖНФ матрицы А, а также ее собственные и корневые подпространства,

.

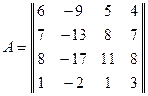Построим характеристический многочлен этой матрицы:

.

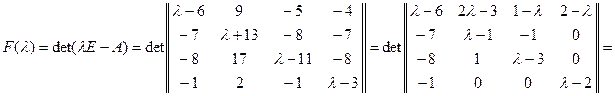
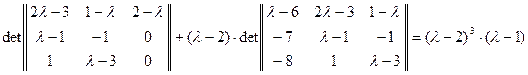Отсюда видно, что собственными значениями будут 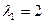и 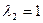, причем первое трехкратное а второе однократное. Это значит, что корневое подпространство имеет размерность 3, а имеет размерность 1 и заведомо совпадает с собственным подпространством. Найдем сначала собственные подпространства. Для этого решаем уравнение 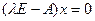. Задавая вектор х матричным образом в виде 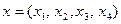и используя матрицу с 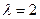, а затем с получаем две однородные системы линейных алгебраических уравнений, общее решение которых и дает представление о соответствующих собственных подпространствах. Строя фундаментальные системы решений, выписываем подпространства в виде линейных оболочек ФСР. Итак, для :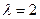

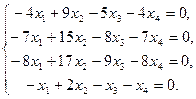
Решая систему методом Гаусса в итоге получим общее решение:

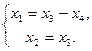
Тогда ФСР, например, такая: 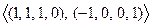. И собственное подпространство для 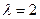получается таким: . При этом .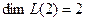

Интересно то, что уже сейчас можно представить ЖНФ матрицы А. Действительно, в силу малой размерности можно представить конфигурацию его корневого базиса, а именно:

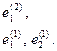
Первый этаж составляют базисные векторы собственного подпространства. Их всего два, поэтому должны существовать векторы высоты 2. Поэтому нарисуем ЖНФ.

.

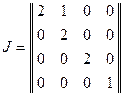В ней присутствует одна клетка Жордана второго порядка и одна первого порядка для 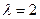, а для лишь одна клетка первого порядка.

Получим собственное подпространство для . Имеем:

Решая систему, находим:

Откуда ФСР есть 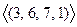и собственное подпространство для таково:

.

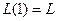
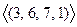С ним же совпадает, как было сказано, и соответствующее корневое подпространство.

Для того, что найти корневое подпространство для 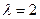требуется решить уравнение

.

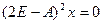Возведем во вторую степень матрицу 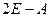и запишем соответствующую однородную систему уравнений:

.

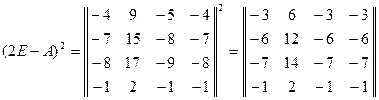Тогда, очевидно, получим систему вида:

.

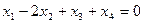Это система ранга 1, поэтому общее решение должно иметь размерность 3, что вполне согласуется с теорией.

ФСР: . .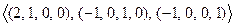

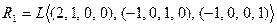Если бы пришлось пользоваться формулой для подсчета количества клеток, то это уместно делать только для 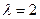. Тогда вычислим . Но 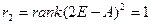, , 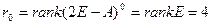. В итоге получаем, что 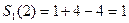. Значит, будет лишь одна клетка первого порядка для 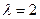, и тогда остается лишь одна клетка второго порядка. Хотя можно подсчитать и 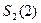. Для этого потребуется знать 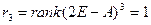, поэтому .