ЛИНЕЙНЫЕ ОПЕРАТОРЫ В КОНЕЧНОМЕРНЫХ ПРОСТРАНСТВАХ 3 страница
Пример 9.13. Если 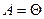 , то любой ненулевой вектор пространства является собственным, отвечающим собственному значению
, то любой ненулевой вектор пространства является собственным, отвечающим собственному значению 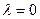 . Действительно,
. Действительно,
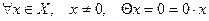 .
.
Пример 9.14. Если  , то тоже любой ненулевой вектор пространства является собственным, отвечающим собственному значению
, то тоже любой ненулевой вектор пространства является собственным, отвечающим собственному значению 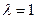 . Именно
. Именно
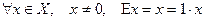 .
.
Пример 9.15. Пусть оператор 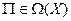 есть оператор прямого проектирования на подпространство
есть оператор прямого проектирования на подпространство 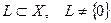 . Тогда
. Тогда  , где
, где 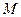 – прямое дополнение к
– прямое дополнение к 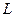 в Х.
в Х.
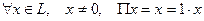 ,
,
 .
.
Пример 9.16. Пусть 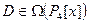 – оператор дифференцирования в пространстве многочленов. Если
– оператор дифференцирования в пространстве многочленов. Если  ,
,  , является собственным вектором, то должно выполняться условие
, является собственным вектором, то должно выполняться условие
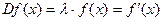 .
.
Но тогда понятно, что собственными векторами такого оператора служат многочлены нулевой степени и только они. Собственное значение при этом равно нулю.
Можно подумать, что каждый оператор 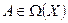 обладает собственными векторами. Однако это не так. В этом можно легко убедиться на следующем геометрическом примере.
обладает собственными векторами. Однако это не так. В этом можно легко убедиться на следующем геометрическом примере.
Пример 9.17. Пусть в пространстве 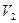 задан оператор поворота векторов положительном направлении на угол
задан оператор поворота векторов положительном направлении на угол 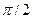 . Это линейный оператор в вещественном пространстве. Образ любого ненулевого вектора при этом будет ортогонален прообразу, т.е., собственных векторов такой оператор иметь не может.
. Это линейный оператор в вещественном пространстве. Образ любого ненулевого вектора при этом будет ортогонален прообразу, т.е., собственных векторов такой оператор иметь не может.
Лемма 9.12. Совокупность собственных векторов линейного оператора 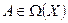 , отвечающих одному собственному значению
, отвечающих одному собственному значению 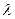 , пополненная нулевым вектором, является подпространством в Х и называется собственным подпространством оператора, соответствующим собственному значению
, пополненная нулевым вектором, является подпространством в Х и называется собственным подпространством оператора, соответствующим собственному значению 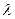 .
.
Доказательство тривиально.
Пример 9.18. У оператора 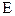 собственным будет все пространство Х.
собственным будет все пространство Х.
Пример 9.19. У оператора прямого проектирования из примера 9.15 два собственных подпространства 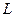 и
и 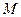 , отвечающих собственным значениям соответственно
, отвечающих собственным значениям соответственно 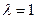 и
и 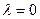 .
.
Определение 9.17. Множество собственных значений линейного оператора называется его спектром.
Пример 9.20. Спектр оператора из примера 9.15 есть  .
.
С понятием собственного вектора можно связать понятие линейной независимости системы, что ввиду важности последнего может быть использовано в дальнейшем. Такую связь задает
Теорема 9.10. Пусть 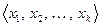 будет системой собственных векторов оператора
будет системой собственных векторов оператора 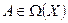 , отвечающих попарно различным собственным значениям, т.е.,
, отвечающих попарно различным собственным значениям, т.е., 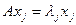 , где
, где 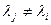 для
для 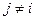 ,
, 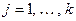 . Тогда система
. Тогда система 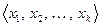 линейно независима.
линейно независима.
Доказательство. Докажем индукцией по 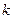 . Если
. Если 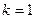 , то линейная независимость системы
, то линейная независимость системы  следует из соответствующих определений. Пусть теорема справедлива для всех
следует из соответствующих определений. Пусть теорема справедлива для всех 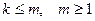 . Докажем теорему для случая
. Докажем теорему для случая 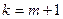 . Не ограничивая общности рассуждений будем считать, что
. Не ограничивая общности рассуждений будем считать, что 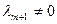 . Составим линейную комбинацию векторов системы
. Составим линейную комбинацию векторов системы 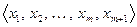 и приравняем ее нулю. Имеем
и приравняем ее нулю. Имеем
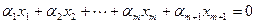 . (9.5)
. (9.5)
Применим к обеим частям равенства оператор  и воспользуемся его линейностью. Получим
и воспользуемся его линейностью. Получим
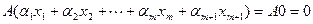 ,
,
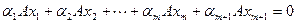 ,
,
и наконец,
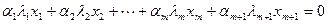 .
.
Умножим обе части равенства (9.5) на 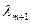 и вычтем из последнего. Это дает
и вычтем из последнего. Это дает
 .
.
Система 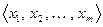 по предположению индукции ЛНЗ, поэтому в последней линейной комбинации все коэффициенты равны нулю. Но так как
по предположению индукции ЛНЗ, поэтому в последней линейной комбинации все коэффициенты равны нулю. Но так как 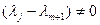 , для
, для  , то
, то 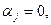
 . Таким образом, от исходной линейной комбинации остается одно слагаемое:
. Таким образом, от исходной линейной комбинации остается одно слагаемое: 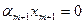 . Откуда
. Откуда 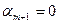 ввиду того, что
ввиду того, что  , как собственный вектор. Теперь по критерию ЛНЗ получаем требуемое, а по принципу индукции доказываем теорему для любого натурального
, как собственный вектор. Теперь по критерию ЛНЗ получаем требуемое, а по принципу индукции доказываем теорему для любого натурального 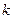 .
.
Особенно интересен случай, когда 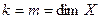 . Тогда получаем базис, целиком состоящий из собственных векторов. Но такой базис может получиться и для одного собственного значения, примером чего является оператор
. Тогда получаем базис, целиком состоящий из собственных векторов. Но такой базис может получиться и для одного собственного значения, примером чего является оператор 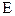 .
.
Определение 9.18. Базис линейного пространства, целиком состоящий из собственных векторов линейного оператора, действующего в этом пространстве, называется собственным базисом этого оператора.
Определение 9.19. Оператор, обладающий собственным базисом, называется диагонализируемым, или оператором простой структуры.
Теорема 9.11 (критерий диагонализируемости линейного оператора).
Линейный оператор диагонализируем тогда и только тогда, когда существует базис, в котором его матрица диагональная.
Доказательство. Необходимость. Пусть оператор А диагонализируем. Тогда у него есть собственный базис: 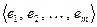 . Запишем соотношения (9.2) для этого базиса.
. Запишем соотношения (9.2) для этого базиса.
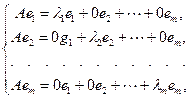 (9.6)
(9.6)
где 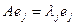 ,
,  . Отсюда матрица
. Отсюда матрица 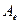 имеет вид:
имеет вид:
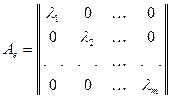 . (9.7)
. (9.7)
Достаточность. Если матрица оператора диагональна, то она имеет вид (9.7). Тогда восстанавливая по ней соотношения типа (9.2), т.е., (9.6) видим, что базис 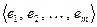 оказывается собственным для данного оператора. Что завершает доказательство теоремы.
оказывается собственным для данного оператора. Что завершает доказательство теоремы.
Характеристический многочлен линейного оператора
Нахождение собственных векторов удобно начинать с вычисления соответствующих собственных значений. Пусть 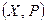 – линейное пространство и оператор
– линейное пространство и оператор 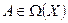 имеет собственный вектор х, отвечающий собственному значению
имеет собственный вектор х, отвечающий собственному значению 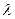 . Таким образом,
. Таким образом, 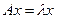 . Это равенство можно переписать иначе:
. Это равенство можно переписать иначе:
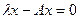 ,
,
или
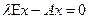 ,
,
что означает по правилу суммы операторов
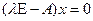 .
.
Отсюда получаем (ввиду неравенства нулю вектора х), что оператор 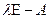 – вырожденный, т.е.,
– вырожденный, т.е., 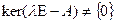 . Зафиксируем какой-либо базис в пространстве Х. Скажем –
. Зафиксируем какой-либо базис в пространстве Х. Скажем – 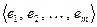 . Тогда в этом базисе у оператора появляется матрица
. Тогда в этом базисе у оператора появляется матрица 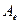 . И по соответствию между действиями над операторами и соответствующими им матрицами находим, что матрица
. И по соответствию между действиями над операторами и соответствующими им матрицами находим, что матрица 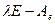 в свою очередь вырожденная, т.е.,
в свою очередь вырожденная, т.е., 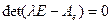 . Покажем, что левая часть последнего равенства не зависит от выбора базиса. Действительно, если выбрать другой базис, например,
. Покажем, что левая часть последнего равенства не зависит от выбора базиса. Действительно, если выбрать другой базис, например, 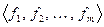 и определить
и определить 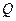 как матрицу перехода от
как матрицу перехода от 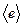 к
к 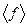 , то для новой матрицы
, то для новой матрицы 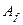 будем иметь соотношение
будем иметь соотношение  . Построим аналогичный определитель с матрицей
. Построим аналогичный определитель с матрицей 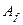 . Тогда находим, что
. Тогда находим, что
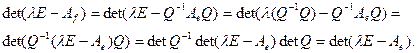
Таким образом, выражение 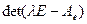 лишь формально зависит от выбора базиса. Вычисляя это определитель, получим
лишь формально зависит от выбора базиса. Вычисляя это определитель, получим
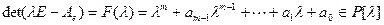 . (9.8)
. (9.8)
Учитывая тот факт, что коэффициенты полученного многочлена не зависят от выбора базиса и способа вычисления определителя, они являются характеристиками оператора, а сам многочлен называется характеристическим многочленом данного оператора. Эти коэффициенты можно явно представить, Например, 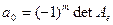 .
.
Итак, каждое собственное значение линейного оператора А обязано быть корнем его характеристического многочлена. С другой стороны, если выбрать некоторый корень этого многочлена 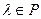 , то понятно, что
, то понятно, что
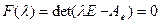 .
.
Значит, матрица 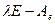 – вырожденная, а с ней и оператор
– вырожденная, а с ней и оператор 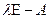 вырожден, т.е., существует вектор
вырожден, т.е., существует вектор  такой, что
такой, что
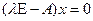 ,
,
откуда сразу получаем, что 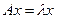 , а это говорит о том, что вектор х – собственный, отвечающий собственному значению
, а это говорит о том, что вектор х – собственный, отвечающий собственному значению 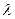 . Следовательно, получена
. Следовательно, получена
Теорема 9.12.
Корни характеристического многочлена линейного оператора, действующего в пространстве над полем Р, лежащие в поле Р, и только они являются собственными значениями этого оператора.
Возникает естественный вопрос: если каждый линейный оператор обладает характеристическим многочленом, то всякий ли многочлен 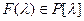 степени
степени 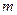 является характеристическим для некоторого оператора в
является характеристическим для некоторого оператора в 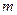 - мерном пространстве над полем Р? Ответ оказывается положительным. Такой многочлен (если пользоваться выражением (9.8)) доставляет матрица
- мерном пространстве над полем Р? Ответ оказывается положительным. Такой многочлен (если пользоваться выражением (9.8)) доставляет матрица
 .
.
Непосредственное вычисление 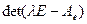 дает выражение (9.8). Эта матрица называется матрицей Фробениуса.
дает выражение (9.8). Эта матрица называется матрицей Фробениуса.
Как известно, не в каждом поле заданный многочлен может иметь корень. И, следовательно, соответствующий оператор иметь собственный вектор. Посмотрим на пример оператора поворота с такой вот алгебраической точки зрения.
Пример 9.21. Выберем в пространстве 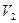 ортогональный базис
ортогональный базис 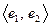 ,
, 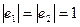 , и построим соотношения (9.2):
, и построим соотношения (9.2):
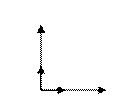
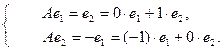
Отсюда получаем матрицу 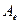 :
:
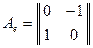 .
.
Тогда
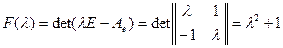 .
.
Так как пространство 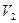 вещественное, а многочлен
вещественное, а многочлен 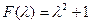 не имеет вещественных корней, то оператор А не имеет собственных значений, а значит и собственных векторов.
не имеет вещественных корней, то оператор А не имеет собственных значений, а значит и собственных векторов.
Совсем другое дело, если рассматривать операторы, действующие в комплексном пространстве. В это случае основное поле – поле С – алгебраически замкнуто. Каждый многочлен положительной степени имеет в нем корень. Тогда и соответствующие операторы обладают собственными значениями, и, значит, собственными векторами. Более того, если многочлен имеет 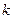 попарно различных корней, то соответствующий оператор имеет ровно
попарно различных корней, то соответствующий оператор имеет ровно 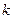 собственных подпространств. Все это приводит к тому, что естественно заниматься операторами в комплексных пространствах.
собственных подпространств. Все это приводит к тому, что естественно заниматься операторами в комплексных пространствах.
Инвариантные подпространства
Получив в свое распоряжение понятие собственного подпространства, сделаем попытку некоторого обобщения его.
Определение 9.20. Пусть 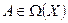 и
и 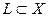 – подпространство в Х. Тогда
– подпространство в Х. Тогда 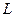 называется инвариантным подпространством относительно оператора А, если для любого
называется инвариантным подпространством относительно оператора А, если для любого  .
.
Пример 9.22. В качестве тривиальных инвариантных подпространств выступают Х и 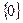 .
.
Пример 9.23. Ядро и образ каждого линейного оператора являются инвариантными подпространствами.
Пример 9.24. Собственные подпространства являются инвариантными для соответствующего оператора.
В дальнейшем появятся другие примеры инвариантных подпространств, а пока покажем, что можно получить уже из самого определения. Пусть 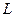 есть нетривиальное инвариантное подпространство в Х. Разложим Х в прямую сумму:
есть нетривиальное инвариантное подпространство в Х. Разложим Х в прямую сумму:
 , (9.9)
, (9.9)
где М – некоторое прямое дополнение к 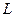 в Х. Зададим базисы в
в Х. Зададим базисы в 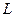 и М:
и М:
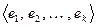 и
и 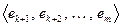 .
.
Построим соотношения типа (9.2). Имеем

В объединенном базисе матрица оператора будет иметь вид:
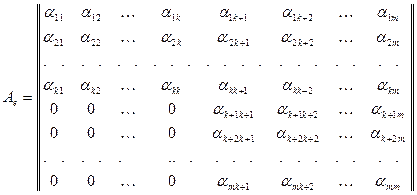 .
.
Легко видеть, что матрица имеет блочный вид, именно:
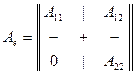 , (9.10)
, (9.10)
 ,
, 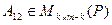 ,
, 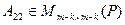 ,
, 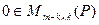 .
.
Таким образом, наличие инвариантного подпространства дает при соответствующем выборе базиса блок нулей в матрице оператора. А если и подпространство М является инвариантным, то матрица приобретает клеточно-диагональный вид:
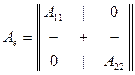 .
.
Естественно, что здесь можно говорить о существенном упрощении матрицы оператора. В дальнейшем нашей задачей станет достижение результата о гарантированном разложении пространства в прямую сумму инвариантных подпространств. Правда, это можно будет доказать для любого оператора, действующего в комплексном пространстве. Поэтому дальнейшие усилия в этом направлении и будут касаться именно таких операторов. Хотя и в общем случае такое возможно, что легко видно для диагонализируемых операторов.
Определение 9.21. Пусть 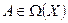 и
и 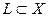 – инвариантное подпространство в Х. Тогда оператор
– инвариантное подпространство в Х. Тогда оператор 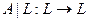 такой, что для любого
такой, что для любого 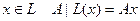 называется оператором, индуцированным, или порожденным, оператором
называется оператором, индуцированным, или порожденным, оператором  . Оператор
. Оператор  при этом называется порождающим.
при этом называется порождающим.
Индуцированный оператор отличается от порождающего в основном пространством, в котором действует, и, несмотря на некоторую искусственность, является удобным инструментом исследования. В частности, если исходный оператор действует в комплексном пространстве и имеет несколько инвариантных подпространств, то на них можно определить индуцированные операторы, которые в свою очередь рассматриваются как операторы в комплексных пространствах, поэтому имеют в них собственные векторы и, значит, порождающий оператор в каждом нетривиальном инвариантном подпространстве имеет по собственному вектору. Индуцированные операторы обладают и характеристическими многочленами, связь которых с характеристическим многочленом порождающего оператора задает следующая
Теорема 9.13.
Пусть 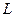 – нетривиальное инвариантное подпространство линейного оператора
– нетривиальное инвариантное подпространство линейного оператора  . Тогда характеристический многочлен оператора, индуцированного на
. Тогда характеристический многочлен оператора, индуцированного на 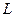 , является делителем характеристического многочлена порождающего оператора.
, является делителем характеристического многочлена порождающего оператора.
Доказательство. Пусть в пространстве задано разложение (9.9), базис 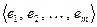 как объединение базисов
как объединение базисов 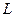 и М. Тогда матрица оператора
и М. Тогда матрица оператора 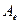 будет иметь в этом базисе вид (9.10). Характеристический многочлен оператора можно представить в следующей форме:
будет иметь в этом базисе вид (9.10). Характеристический многочлен оператора можно представить в следующей форме:
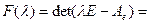
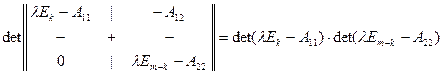 .
.
Вычисление получено по теореме Лапласа разложением по первым 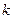 столбцам. Легко представить, что характеристическим многочленом индуцированного оператора является множитель (он же делитель
столбцам. Легко представить, что характеристическим многочленом индуцированного оператора является множитель (он же делитель 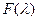 )
) 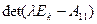 , ибо матрицей этого оператора в базисе
, ибо матрицей этого оператора в базисе 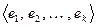 как раз и является матрица-блок
как раз и является матрица-блок 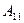 . Таким образом, теорема доказана.
. Таким образом, теорема доказана.
Польза от этой теоремы может быть следующая. Располагая инвариантными подпространствами, можно строить индуцированные операторы и их характеристические многочлены. Деля характеристический многочлен исходного оператора на характеристический индуцированного, понижаем степень вычисления корней многочлена, т.е., собственных значений оператора (например, в комплексном случае).
Треугольная форма матрицы оператора в комплексном пространстве.
Начнем с некоторых полезных лемм. Итогом параграфа будет результат о возможности представления матрицы оператора в комплексном пространстве в треугольном виде.
Лемма 9.13. Ядро и образ операторного многочлена являются инвариантными подпространствами порождающего оператора.
Доказательство. Пусть  будет операторным многочленом оператора
будет операторным многочленом оператора  и
и  – его ядро. Тогда для любого вектора
– его ядро. Тогда для любого вектора 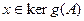 имеем:
имеем:
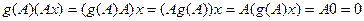 ,
,
т.е., 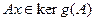 . Это возможно ввиду коммутативности кольца операторных многочленов, порожденных оператором
. Это возможно ввиду коммутативности кольца операторных многочленов, порожденных оператором  (см. т. 9.4) .
(см. т. 9.4) .
Теперь пусть 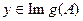 , т.е., существует
, т.е., существует 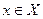 такой, что
такой, что 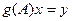 . Тогда
. Тогда
 .
.
Здесь тоже отработала теорема 9.4. Лемма доказана.
Лемма 9.14. Каждое инвариантное подпространство относительно оператора  является таковым и для любого его операторного многочлена, а для оператора
является таковым и для любого его операторного многочлена, а для оператора  справедливо и обратное утверждение.
справедливо и обратное утверждение.
Доказательство. Практически тривиальное.
Лемма 9.15. Если вектор  является собственным вектором оператора
является собственным вектором оператора  , то для любого операторного многочлена
, то для любого операторного многочлена  х также будет собственным, отвечающим собственному значению
х также будет собственным, отвечающим собственному значению 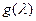 .
.
Доказательство. Пусть 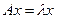 и
и 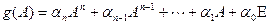 . Тогда
. Тогда
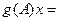
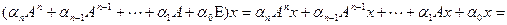
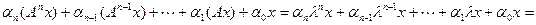
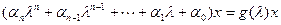 ,
,
Что и требовалось доказать. Здесь воспользовались тривиальным равенством  .
.
Лемма 9.16. Все собственные векторы оператора  , отвечающие собственным значениям, которые являются (не являются) корнями многочлена
, отвечающие собственным значениям, которые являются (не являются) корнями многочлена 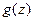 , принадлежат ядру (образу)
, принадлежат ядру (образу)  .
.
Доказательство. Пусть 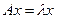 , тогда по лемме 9.15
, тогда по лемме 9.15  . Поэтому, если
. Поэтому, если 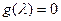 , то
, то  , и
, и 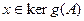 . Иначе, если
. Иначе, если 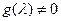 , то
, то  , и
, и 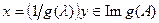 .
.
Дата добавления: 2019-07-26; просмотров: 1246;
