ЛИНЕЙНЫЕ ОПЕРАТОРЫ В КОНЕЧНОМЕРНЫХ ПРОСТРАНСТВАХ 2 страница
Пусть дополнительно задан и базис пространства 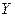 –
– 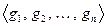 . Разложим образы базисных векторов пространства Х по базису пространства
. Разложим образы базисных векторов пространства Х по базису пространства 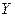 . Получим
. Получим
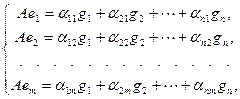 (9.2)
(9.2)
или сокращенно
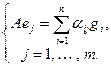
Матрица 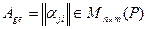 , составленная из коэффициентов разложения образов базисных векторов пространства
, составленная из коэффициентов разложения образов базисных векторов пространства  по базису пространства
по базису пространства 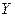 называется матрицей линейного оператора
называется матрицей линейного оператора  в базисах
в базисах  и
и 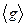 .
.
Очевидно, что матрица 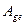 однозначно определяется базисами
однозначно определяется базисами 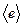 и
и 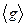 . В другой паре базисов она, вообще говоря, должна быть другой. Этот вопрос детально рассмотрим позже. А пока вернемся к вектору
. В другой паре базисов она, вообще говоря, должна быть другой. Этот вопрос детально рассмотрим позже. А пока вернемся к вектору  . Его образом был некоторый вектор
. Его образом был некоторый вектор 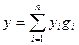 . Снова вернемся к равенству
. Снова вернемся к равенству 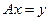 . Это так называемое операторное равенство. Вновь учтем, что
. Это так называемое операторное равенство. Вновь учтем, что 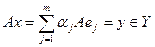 и воспользуемся равенствами (9.2). Получим
и воспользуемся равенствами (9.2). Получим
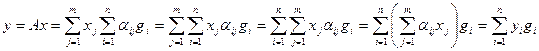 .
.
Откуда в силу основного свойства базиса имеем:
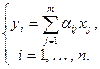 (9.3)
(9.3)
С матричной точки зрения получили соотношение 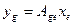 . Это так называемое координатное равенство, очень похожее на операторное. Такое равенство, записанное на языке матричного умножения, позволяет представить действие любого линейного оператора в конечномерных пространствах. Именно это равенство и делает возможным исследование строения линейного оператора через строение его матрицы в подходящей паре базисов.
. Это так называемое координатное равенство, очень похожее на операторное. Такое равенство, записанное на языке матричного умножения, позволяет представить действие любого линейного оператора в конечномерных пространствах. Именно это равенство и делает возможным исследование строения линейного оператора через строение его матрицы в подходящей паре базисов.
Распишем соотношения (9.3) подробно:
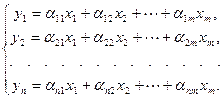
Из этих соотношений легко видно, что так как координатные столбцы векторов-образов линейно выражаются через столбцы матрицы оператора 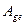 , то ранг оператора совпадает с рангом его матрицы. Если заменить левые части соотношений (9.3) нулями, то решая соответствующую однородную систему линейных алгебраических уравнений получим координатное представление ядра оператора. Как известно, размерность общего решения такой системы есть
, то ранг оператора совпадает с рангом его матрицы. Если заменить левые части соотношений (9.3) нулями, то решая соответствующую однородную систему линейных алгебраических уравнений получим координатное представление ядра оператора. Как известно, размерность общего решения такой системы есть 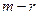 , где
, где 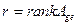 (см. гл.VI,т.6.9 ). Таким образом, дефект оператора есть
(см. гл.VI,т.6.9 ). Таким образом, дефект оператора есть 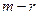 , что подтверждает теорему 9.5.
, что подтверждает теорему 9.5.
Возникает вопрос: всякая ли матрица 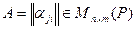 может служить матрицей некоторого линейного оператора, действующего из
может служить матрицей некоторого линейного оператора, действующего из 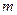 -мерного пространства в
-мерного пространства в  -мерное над полем Р? Ответ положительный. Пусть матрица
-мерное над полем Р? Ответ положительный. Пусть матрица 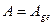 , для которой записаны равенства (9.3). Эти соотношения задают некоторый линейный оператор
, для которой записаны равенства (9.3). Эти соотношения задают некоторый линейный оператор  . Если строить матрицу этого оператора в базисах
. Если строить матрицу этого оператора в базисах 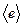 и
и 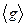 (точнее в их координатных представлениях), то получим как раз матрицу
(точнее в их координатных представлениях), то получим как раз матрицу 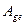 , ибо векторы
, ибо векторы 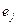 ,
,  имеют в своем базисе вид единичных строк.
имеют в своем базисе вид единичных строк.
Отметим отдельно важный случай операторов из 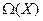 . Здесь, как правило, нет нужды задавать два базиса. Поэтому и матрица строится в одном базисе, когда образы базисных векторов разлагаются по тому же базису. В итоге получаем, например, матрицу в базисе
. Здесь, как правило, нет нужды задавать два базиса. Поэтому и матрица строится в одном базисе, когда образы базисных векторов разлагаются по тому же базису. В итоге получаем, например, матрицу в базисе 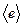 –
– 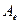 . Координатное равенство имеет при этом вид:
. Координатное равенство имеет при этом вид: 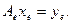
Пример 9.9. Очевидно, что матрицей нулевого оператора  в любой паре базисов будет нулевая матрица соответствующих размеров.
в любой паре базисов будет нулевая матрица соответствующих размеров.
Пример 9.10. Единичный оператор 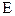 в любом базисе имеет единичную матрицу
в любом базисе имеет единичную матрицу 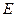 .
.
Пример 9.11. Построим матрицу оператора дифференцирования 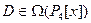 в базисе
в базисе 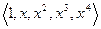 . Вычислим соотношения (9.2).
. Вычислим соотношения (9.2).
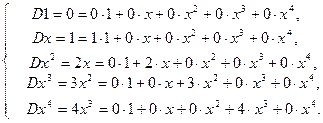
Теперь составим матрицу из коэффициентов разложений:
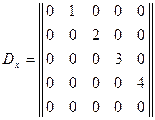 .
.
Продемонстрируем на этом примере применение координатного равенства. Пусть задан многочлен 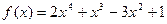 . В выбранном базисе ему отвечает столбец координат
. В выбранном базисе ему отвечает столбец координат
 .
.
Вычислим координатный столбец образа:
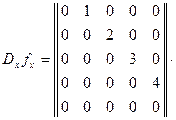
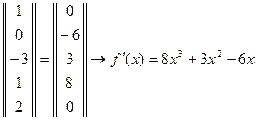 .
.
Пример 9.12. Пусть 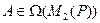 – оператор транспонирования. Зададим единичный базис в
– оператор транспонирования. Зададим единичный базис в 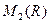 :
: 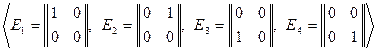 . Выпишем соотношения (9.2):
. Выпишем соотношения (9.2):
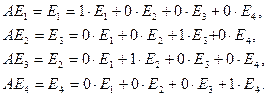
Это дает возможность записать матрицу 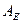 :
:
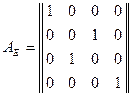 .
.
Если теперь взять произвольную матрицу второго порядка 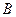 :
:
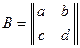 , то
, то 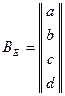 .
.
Тогда 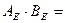
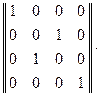
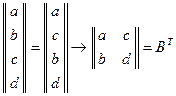 .
.
Соответствие между действиями над операторами и соответствующими матрицами
Для описания указанного выше соответствия введем специальное обозначение. Пусть вектор х в базисе  имеет представление
имеет представление 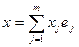 . Тогда обозначим через
. Тогда обозначим через 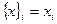 ,
, 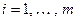 .
.
Пусть теперь заданы два оператора 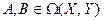 , где
, где 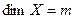 ,
, 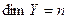 . В пространствах Х и
. В пространствах Х и 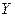 зафиксируем соответствующие базисы
зафиксируем соответствующие базисы 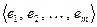 и
и 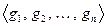 . В этих базисах опишем матрицы операторов:
. В этих базисах опишем матрицы операторов: 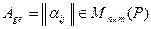 и
и 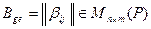 . Пусть
. Пусть 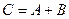 и
и  . Рассмотрим элемент
. Рассмотрим элемент  .
.
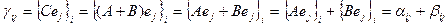 ,
,
т.е., 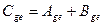 .
.
Лемма 9.6. Сумме операторов отвечает сумма их матриц в заданной паре базисов.
Если рассмотреть оператор 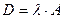 и его матрицу
и его матрицу 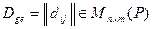 , легко находим, что
, легко находим, что
 .
.
Отсюда
Лемма 9.7. Матрица произведения оператора на число равна матрице этого оператора, умноженной на это же число для заданной пары базисов.
Наконец, рассмотрим произведение операторов. Пусть 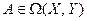 ,
, 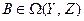 и
и  , где
, где  . Зададим базисы в пространствах
. Зададим базисы в пространствах 
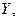
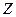 соответственно:
соответственно: 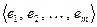 ,
, 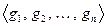 и
и 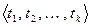 . В этих базисах зафиксируем матрицы операторов
. В этих базисах зафиксируем матрицы операторов 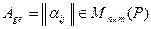 ,
,  и
и  . Запишем для удобства рассуждений соотношения типа (9.2). Именно:
. Запишем для удобства рассуждений соотношения типа (9.2). Именно: 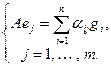
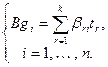
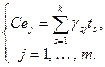 .
.
Тогда
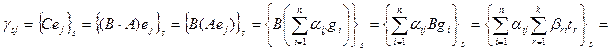
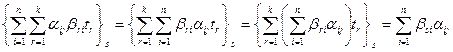 .
.
Здесь видно, что произвольный элемент матрицы  выступает как элемент произведения матриц
выступает как элемент произведения матриц 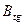 и
и 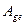 . Таким образом, матрица
. Таким образом, матрица 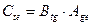 . Отсюда лемма:
. Отсюда лемма:
Лемма 9.8. Матрица произведения операторов равна произведению матриц сомножителей в соответствующим образом подобранных базисах.
Замечание. Становится теперь ясным, отчего сравнительно сложно определялось произведение матриц. Оказалось, что это произведение отражает операцию произведения линейных операторов.
Теорема 9.8.
Пусть 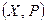 и
и 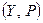 – два линейных пространства,
– два линейных пространства, 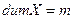 ,
, 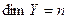 . Тогда
. Тогда 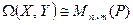 , т.е., пространство операторов изоморфно пространству матриц.
, т.е., пространство операторов изоморфно пространству матриц.
Доказательство. Зафиксируем базисы в указанных пространствах: 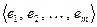 и
и 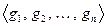 . Для данного оператора А запишем матрицу в данных базисах –
. Для данного оператора А запишем матрицу в данных базисах – 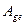 . И учредим соответствие
. И учредим соответствие 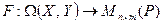 по правилу
по правилу 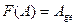 . Очевидно, что это соответствие является отображением. Отображение
. Очевидно, что это соответствие является отображением. Отображение  сюръективно, ибо, как было указано, каждая матрица из
сюръективно, ибо, как было указано, каждая матрица из 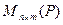 является матрицей какого-либо линейного оператора из
является матрицей какого-либо линейного оператора из  в данной паре базисов. Отображение
в данной паре базисов. Отображение  – инъективно, так как из координатного равенства следует, что если равны матрицы двух операторов в одной паре базисов, то равны и операторы. Таким образом, получается, что
– инъективно, так как из координатного равенства следует, что если равны матрицы двух операторов в одной паре базисов, то равны и операторы. Таким образом, получается, что  – биекция. Ее линейность следует из лемм 9.6 и 9.7. Тем самым теорема доказана.
– биекция. Ее линейность следует из лемм 9.6 и 9.7. Тем самым теорема доказана.
Следствие. 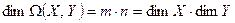 .
.
Переход к новым базисам
Завершая предварительное описания понятия матрицы оператора остановимся на вопросе б изменении матрицы при переходе к новой паре базисов. Пусть задан оператор 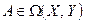 и его матрица
и его матрица 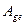 в базисах
в базисах 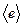 и
и 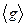 . Введем новую пару базисов –
. Введем новую пару базисов – 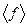 и
и 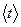 . Пусть матрицей перехода от базиса
. Пусть матрицей перехода от базиса 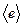 к базису
к базису 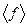 будет
будет 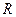 , а от
, а от 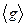 к
к 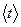 –
– 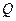 . Тогда для произвольного
. Тогда для произвольного 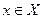 пусть
пусть 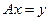 и
и 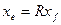 , а
, а 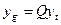 . Для обеих пар базисов имеем два координатных равенства:
. Для обеих пар базисов имеем два координатных равенства:
 и
и 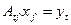 .
.
Подставим в первое равенство выражения для  и
и 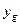 . Получим
. Получим
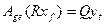 ,
,
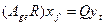 .
.
Умножая обе части последнего равенства на  слева и сравнивая со вторым координатным равенством, получим
слева и сравнивая со вторым координатным равенством, получим
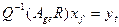 ,
,
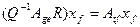 .
.
Теперь, если для произвольного столбца 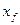 имеем такое равенство, то
имеем такое равенство, то
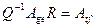 . (9.4)
. (9.4)
Это и есть та формула, которая связывается матрицы одного и тог же оператора для разных пар базисов. В случае, если 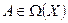 , то нет нужды, как уже говорилось, в двух базисах. Поэтому соответствующая формула упрощается, а именно:
, то нет нужды, как уже говорилось, в двух базисах. Поэтому соответствующая формула упрощается, а именно:
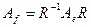 .
.
Эквивалентность и подобие матриц
Основной задачей этого параграфа является выяснение вопроса о простейшем виде матрицы оператора 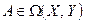 .
.
Определение 9.14. Пусть заданы две матрицы 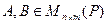 .Матрица В называется эквивалентной матрице А, если существуют такие матрицы
.Матрица В называется эквивалентной матрице А, если существуют такие матрицы 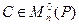 и
и 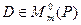 такие, что
такие, что 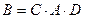 .
.
Лемма 9.9. Бинарное отношение эквивалентности матриц на множестве матриц данного размера над полем Р есть отношение эквивалентности.
Доказательство. Рефлексивность проверяется равенством 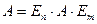 . Симметричность следует из равенства
. Симметричность следует из равенства 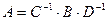 , ибо С и
, ибо С и 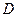 – невырожденные. Пусть теперь
– невырожденные. Пусть теперь 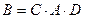 и
и  . Тогда
. Тогда 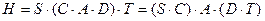 , что означает эквивалентность матрицы
, что означает эквивалентность матрицы 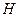 матрице А. Таким образом, транзитивность тоже выполняется, ибо
матрице А. Таким образом, транзитивность тоже выполняется, ибо 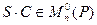 и
и 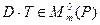 как произведения невырожденных матриц одного порядка.
как произведения невырожденных матриц одного порядка.
Лемма 9.10 (первый критерий эквивалентности матриц).
Две матрицы одного размера над полем Р эквивалентны тогда и только тогда, когда являются матрицами одного линейного оператора в подходящим образом выбранных базисах.
Доказательство. Необходимость. Если матрица 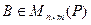 эквивалентна матрице
эквивалентна матрице 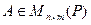 , то выполняется равенство
, то выполняется равенство 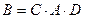 с
с  и
и 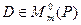 . Если рассматривать матрицу А как матрицу
. Если рассматривать матрицу А как матрицу 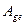 линейного оператора из
линейного оператора из 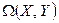 в некоторых базисах
в некоторых базисах 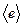 и
и 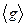 , то интерпретируя матрицы
, то интерпретируя матрицы 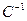 и
и 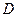 как матрицы перехода к новой паре базисов, получаем требуемое.
как матрицы перехода к новой паре базисов, получаем требуемое.
Достаточность. Если матрицы А и В – это матрицы одного оператора для разных пар базисов, то равенство (9.4) доставляет требуемое.
Теорема 9.9 (второй критерий эквивалентности матриц).
Две матрицы одного размера над полем Р эквивалентны тогда и только тогда, когда имеют одинаковые ранги.
Доказательство. Необходимость. Пусть матрица 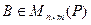 эквивалентна матрице
эквивалентна матрице 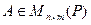 , то для некоторых
, то для некоторых  и
и 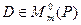
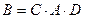 .
.
Вычислим ранг В.
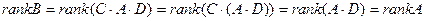 .
.
Здесь воспользовались следствием из теоремы 6.2 об умножении на невырожденную матрицу.
Достаточность. Пусть теперь 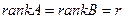 для матриц из предыдущей части доказательства. Покажем большее. Покажем, матрицы В и А эквивалентны каждая матрице
для матриц из предыдущей части доказательства. Покажем большее. Покажем, матрицы В и А эквивалентны каждая матрице 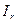 , где
, где
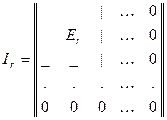 .
.
Здесь в левом верхнем углу расположена единичная матрица порядка 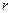 , а остальные элементы равны нулю.
, а остальные элементы равны нулю.
Действительно, пусть 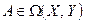 линейный оператор, действующий из
линейный оператор, действующий из 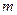 - мерного пространства Х в
- мерного пространства Х в  - мерное пространство
- мерное пространство 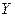 . И пусть матрица А будет матрицей этого оператора в базисах
. И пусть матрица А будет матрицей этого оператора в базисах 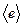 и
и 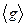 . Таким образом,
. Таким образом, 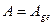 . Тогда ранг этого оператора равен числу
. Тогда ранг этого оператора равен числу 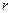 . Следовательно, при известной перенумерации базисных векторов можно считать, что
. Следовательно, при известной перенумерации базисных векторов можно считать, что 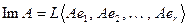 . При этом
. При этом
 .
.
Построим новую пару базисов для записи матрицы оператора А : 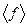 и
и 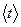 . Положим в Х
. Положим в Х
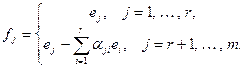
А в пространстве 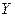
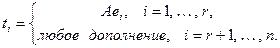
В этой паре базисов матрица оператора А приобретает вид 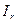 .Формально, надо бы доказать, что система
.Формально, надо бы доказать, что система 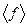 – базисная, но оставим это студентам. Теорема доказана.
– базисная, но оставим это студентам. Теорема доказана.
Теорема 9.9 говорит о том, какова простейшая форма записи матрицы оператора из 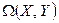 . Это как раз матрица
. Это как раз матрица 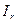 с точностью до перестановки векторов в базисе. В силу свойства транзитивности отношения эквивалентности матриц эта матрица подобна любой матрице ранга
с точностью до перестановки векторов в базисе. В силу свойства транзитивности отношения эквивалентности матриц эта матрица подобна любой матрице ранга 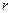 над полем Р. Такой простой вид возможен от того, что базисы в Х и
над полем Р. Такой простой вид возможен от того, что базисы в Х и 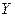 выбираются независимо. Случай операторов из
выбираются независимо. Случай операторов из 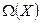 гораздо более сложен. Ему будет посвящено все остальное исследование этой главы.
гораздо более сложен. Ему будет посвящено все остальное исследование этой главы.
Определение 9.15. Матрица  называется подобной матрице
называется подобной матрице 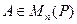 , если существует такая матрица
, если существует такая матрица 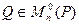 такая, что
такая, что 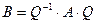 . Матрица
. Матрица 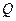 называется матрицей подобного преобразования.
называется матрицей подобного преобразования.
Лемма 9.10. Бинарное отношение подобия матриц на множестве всех квадратных матриц данного порядка над полем Р есть отношение эквивалентности.
Доказательство очень похоже на доказательство леммы 9.9.
Лемма 9.11 (первый критерий подобия матриц).
Две квадратные матрицы одного порядка над полем Р подобны тогда и только тогда, когда являются матрицами одного линейного оператора в подходящих базисах.
Доказательство и этой леммы во многом повторяет доказательство леммы 9.10.
Вопрос о подобии матриц достаточно сложен и будет в дальнейшем увязан с теорией операторов из 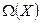 . Здесь же будет решаться и вопрос о наиболее простом виде матрицы таких операторов.
. Здесь же будет решаться и вопрос о наиболее простом виде матрицы таких операторов.
Собственные подпространства
Начнем изучать операторы из 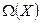 . Рассмотрим один специальный случай, когда образ вектора коллинеарен прообразу. Оказывается, что такая возможность имеет важные последствия.
. Рассмотрим один специальный случай, когда образ вектора коллинеарен прообразу. Оказывается, что такая возможность имеет важные последствия.
Определение 9.16. Пусть 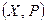 – линейное пространство и
– линейное пространство и 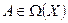 . Тогда вектор
. Тогда вектор 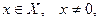 называется собственным вектором оператора
называется собственным вектором оператора  , отвечающим собственному значению
, отвечающим собственному значению 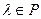 , если выполнено условие
, если выполнено условие 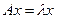 .
.
Дата добавления: 2019-07-26; просмотров: 818;
