ЛИНЕЙНЫЕ ОПЕРАТОРЫ В КОНЕЧНОМЕРНЫХ ПРОСТРАНСТВАХ 1 страница

Введение

Идея линейности пронизывает всю математику. В данном случае эта идея формально выступает в виде специальных отображений в линейных пространствах, которые назовем в свою очередь линейными. Построенная теория имеет много точек соприкосновения с другими математическими теориями, а в данном курсе существенно использует материал предыдущих глав. Если не оговорено противное, везде используется числовое поле Р.

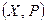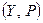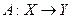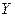Определение 9.1. Пусть заданы два линейных пространства над одним и тем же полем и . Отображение пространства в пространство называется линейным, или линейным оператором, если для любых 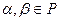и любых 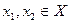выполнено

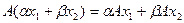. (9.1)

Как правило, в дальнейшем будет использоваться термин «линейный оператор» или просто «оператор», подразумевая линейность последнего. Обозначать операторы будем большими латинскими буквами: А, В, С, … Кроме того, в простейших случаях будем экономить скобки, например, вместо будем писать .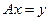

Равенство (9.1) иногда выгодно расписать в два:

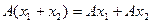, аддитивное свойство А;

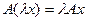, свойство однородности А;

, .

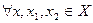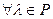Определение 9.2. Оператор 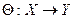, определяемый соотношением 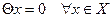называется нулевым оператором.

Такой оператор, очевидно, линеен.

Определение 9.3 Оператор 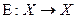, определяемый соотношением 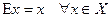называется единичным.

Такой оператор тоже линеен.

Определение 9.4. Оператор , определяемы соотношением 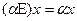, 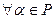называется скалярным.

Скалярный оператор тоже линеен и при 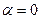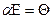, а при .

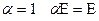Приведенные определения стандартных операторов являются простейшими примерами линейных отображений. Рассмотрим более сложные примеры.

Пример 9.1. Изоморфизм линейных пространств (см. гл.V).

Пример 9.2. Пусть 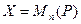, 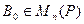. Зададим отображение 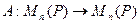соотношением: 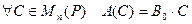. Получим линейный оператор.

Пример 9.3. Оператор транспонирования квадратных матриц из 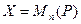является линейным, если вспомнить свойства транспонирования.

Пример 9.4. Пусть 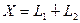– прямая сумма подпространств. Определим оператор 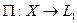прямого проектирования соотношением: 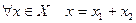, где 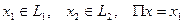. Это, очевидно, линейный оператор.

Пример 9.5. Пусть 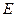евклидово пространство и 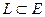подпространство в 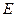, тогда оператор 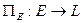определим равенством: 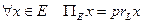. Оператор назовем оператором ортогонального проектирования. В силу свойства проекции он является линейным.

Пример 9.6. Пусть 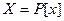, оператор 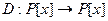определим равенством: 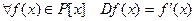. В силу свойств производной оператор является 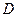линейным.

Пример 9.7. Пусть 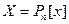, , 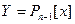. Оператор 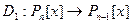вновь определим равенством 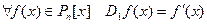. Этот оператор в отличие от предыдущего «работает» в конечномерных пространствах.

Пример 9.8. Пусть 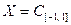, . Оператор 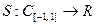определим соотношением: 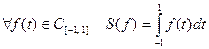. В силу свойств определенного интеграла это линейный оператор. Этот пример приводит к следующему определению.

Определение 9.5. Линейный оператор, действующий из любого пространства в поле, над которым оно задано, называется линейным функционалом.

Пример. 9.8. Пусть 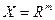, тогда линейным функционалом будет оператор 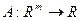, задаваемый условием: .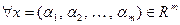

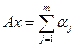Действия над линейными операторами

Равенство линейных операторов есть обычное равенство отображений. На этой основе определим основные операции над линейными операторами. Предварительно договоримся об одном обозначении. Множество всех линейных операторов, действующих из линейного пространства в линейное пространство 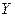обозначим через .Если 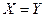, то будем писать .

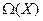Определение 9.6. Пусть 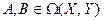. Тогда суммой операторов и 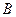называется отображение 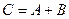такое, что .

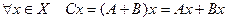Лемма 9.1. Для любых .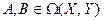

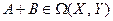Теорема 9.1. 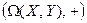– абелева группа.

Это простое упражнение на проверку аксиом группы. Алгебраичность операции следует из леммы 9.1. Нейтральным элементом будет оператор – нулевой.

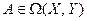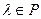Определение 9.7. Пусть и . Тогда произведением числа 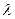на оператор называется отображение такое, что .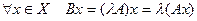

Лемма 9.2. Для любых 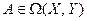и .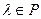

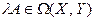Теорема 9.2. Пусть 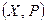и 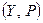– два линейных пространства. Тогда множество относительно сложения линейных операторов и умножения их на числа из поля Р образует линейное пространство над полем Р.

Это тоже простое упражнение на проверку аксиом линейного пространства. Здесь первую группу аксиом обеспечивает теорема 9.1.

Определение 9.8. Пусть 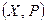, , 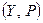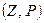– линейные пространства, 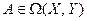и 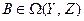. Тогда произведением операторов 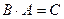называется композиция отображений В и А. Таким образом, .

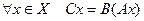Лемма 9.3. Для любых 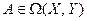и .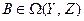

Теорема 9.3. Тройка 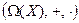образует ассоциативное кольцо с единицей.

Здесь теорема 9.1 задает аддитивную группу кольца. Алгебраичность умножения обеспечивается леммой 9.3. Ассоциативность композиции известна из главы I (см. л. 1.5). Единицей кольца будет оператор 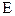. Дистрибутивные законы проверяются тривиально.

Дополнительным свойством, связывающим оба произведения для операторов, служит следующее:

.

Это свойство выполняется, очевидно, и для случая, когда операторы действуют из одного пространства в другое при условии существования композиции .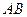

Определение 9.9. Пусть задан многочлен ,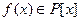

,

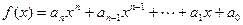и линейный оператор , где Х – пространство над полем 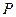. Тогда линейный оператор называется операторным многочленом, порожденным многочленом 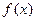и оператором А. Множество таких многочленов обозначим .

Теорема 9.4. Тройка 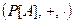образует коммутативное кольцо с единицей.

Проверка аксиом кольца здесь тривиальная. Коммутативность же следует из того, что все операторные многочлены из порождены одним линейным оператором.

Образ и ядро линейного оператора

Образ линейного оператора – это образ отображения. Поэтому нового здесь ничего нет. Таким образом, для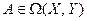

.

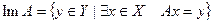Но, тем не менее, справедлива следующая лемма.

Лемма 9.4. Для 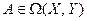– подпространство в .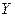

Применение критерия подпространства доказывает эту лемму (см. гл.V, т.5.1). Но так как речь идет о подпространстве конечномерного пространства, то оно должно обладать некоторой размерностью.

Определение 9.10. Размерность образа линейного оператора называется его рангом.

Легко заметить, что для 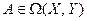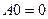, ибо 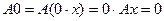. Но могут быть и другие векторы, отображаемые в нулевой вектор. Отсюда

Определение 9.11. Для линейного оператора 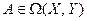совокупность векторов пространства Х, отображаемых в нуль пространства 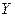, называется ядром оператора А и обозначается . Т.е.,

.

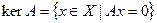Лемма 9.5. Ядро линейного оператора 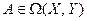есть подпространство в Х.

Здесь также следует применить критерий подпространства. И так же, как в случае с образом, получаем, что ядро должно обладать размерностью. Отсюда новое определение.

Определение 9.12. Размерность ядра линейного оператора называется его дефектом.

Оказывается, что вновь определенные два числа, ранг и дефект, связаны между собой жесткой связью. Именно, имеет место следующая теорема.

Теорема 9.5. Для линейного оператора 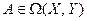справедливо равенство:

.

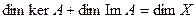Доказательство. Разложим пространство Х в прямую сумму:

,

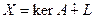где 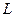– любое прямое дополнение к . Если доказать изоморфизм 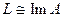, то теорема будет доказана, ибо размерности изоморфных пространств совпадают (см. т.5.9). Действительно, определим отображение 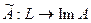правилом: .

Докажем, что 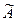– изоморфизм. Линейность этого отображения обеспечивается

линейностью оператора А. Поэтому достаточно доказать его биективность. Из прямой суммы имеем, что любой вектор 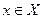можно однозначно представить в виде ,

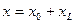где 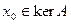, а 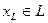. Так как , , 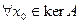то образы векторов из Х поставляются исключительно векторами из 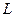. Поэтому отображение 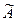сюръективно. С другой стороны, если 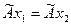для какой-то пары векторов из 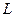, то это значит, что 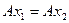, т.е., , а значит, 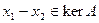, но вектор 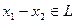. Откуда, в силу прямоты суммы, , т.е., 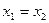, что доказывает инъективность отображения 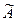. Значит, оно биективно, и теорема доказана.

Мультипликативная группа операторов

В теореме 9.1 была построена аддитивная группа операторов из . Интересно сделать попытку построения мультипликативной группы, но в данном случае придется ограничиться множеством 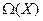. Но оказывается, что этого ограничения недостаточно. Требуется существенно более узкое множество. Причина будет выяснена ниже.

Определение 9.13. Линейный оператор называется невырожденным, если его ядро равно 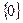, т.е., 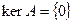. В противном случае он называется вырожденным.

Нам потребуется теорема, позволяющая посмотреть на феномен невырожденности с разных сторон.

Теорема 9 6 (условия невырожденности линейного оператора).

Следующие высказывания для оператора эквивалентны:

1. 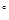Оператор А невырожденный;

2. ;

3. ;

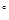
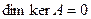4. ;

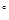
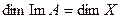5. 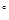А – сюръекция;

6. 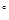А – инъекция;

7. 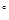А – биекция;

8. 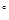А – автоморфизм ( изоморфизм на себя).

Доказательство. Вначале запишем очевидную цепочку заключений, опирающуюся на определение и теорему 9.5:

Невырожденность 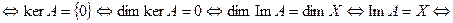А –сюръекция. Докажем теперь инъективность А, исходя из его невырожденности. Рассуждаем от противного. Пусть А не является инъекцией. Тогда найдутся два вектора 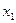и 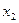такие, чт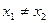о , но 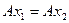, что влечет , т.е. 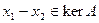, но так как 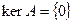, то 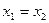. Противоречие доказывает инъективность А. Обратно, пусть теперь А инъективно, но 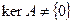. Значит, найдется вектор такой, что 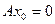. Выберем два различных вектора 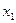и . Очевид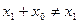но, , но 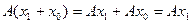. Таким образом получаем противоречие с инъективностью А. Ну а тогда имеем: 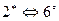. Остальные эквивалентности очевидны. Теорема доказана.

Обозначим множество линейных невырожденных операторов и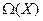з через .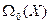

Теперь можно приступать к построению группы.

Теорема 9.7. Пара 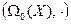группа.

Доказательство. Здесь придется проверить выполнимость аксиом группы. Начнем с алгебраичности операции. Разумеется, любые два оператора из 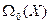можно перемножить. Пусть 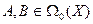. Тогда, если бы существовал вектор такой, ч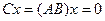то , то 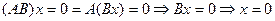, что невозможно. Таким образом, операция умножения алгебраична. Ассоциативность по понятным причинам доказывать не нужно. А нейтральным элементом, очевидно, будет 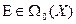. Остается аксиома симметричных элементов. Необходимо, чтобы

.

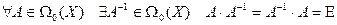Но так как по теореме 9.6 операторы из 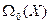представляют собой биекции, то обратимость отображений обеспечена (см. гл. I, т.1.2) . Остается показать, что обратные отображения являются линейными и невырожденными. Сначала выявим свойство линейности. Требуется, чтобы для любых 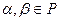и любых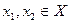

.

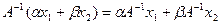Вычислим образы правой и левой части под действием А и пользуясь биективностью А сделаем соответствующее заключение. Имеем

и

.

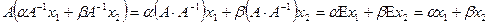В последнем случае воспользовались линейностью . Итак, видим, что образы обеих частей гипотетического равенства равны. Тогда в силу биективности получаем, что прообразы равны, что завершает доказательство линейности.

Невырожденность 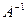следует из того, что если для 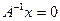, то тогда

.

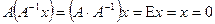Получаем противоречие. Таким образом, теорема полностью доказана.

Замечание. Используя невырожденные операторы можно строить циклические мультипликативные группы. Выбираем порождающий элемент и рассматриваем всевозможные степени этого оператора: .

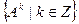Матрица линейного оператора

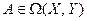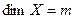Пусть заданы линейный оператор , где , а 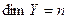и базис пространства Х 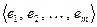. Пусть 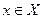любой вектор, и 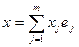. Подействуем оператором на вектор х. Тогда получим . Легко видеть, что произвольный вектор-образ выражается через систему образов базисных векторов, т.е. через систему . Таким образом, описание действия оператора возможно через линейную комбинацию системы . Разовьем эту идею.