На рисунке эту пару не изображаем, а показываем ее момент, полностью определяющий действие самой пары.
Линейная величина 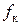 , измеряемая обычно в сантиметрах, называется коэффициентом трения качения.
, измеряемая обычно в сантиметрах, называется коэффициентом трения качения.
Найдём предельное значение тяги Sпр. В предельном положении момент пары трения качения равен моменту вращающей пары:
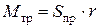 ,
,
где r - радиус катка.
Или
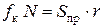 .
.
Откуда находим
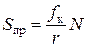 .
.
Качение начнется, если

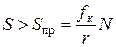 . (29)
. (29)
Качение будет происходить без скольжения, как было отмечено выше, если
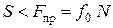 . (30)
. (30)
Итак, при качении без скольжения должны выполняться одновременно условия(29) и (30).
Для большинства материалов 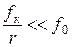 , что хорошо видно из таблицы
, что хорошо видно из таблицы
Поэтому  и, следовательно, условия (29) и (30) не противоречат друг другу.
и, следовательно, условия (29) и (30) не противоречат друг другу.
Таблица Коэффициенты трения скольжения и качения
| № п/п | Материалы тела | Коэффициент трения скольжения | Материалы тела | Коэффициент трения качения |
| 1. | Сталь по стали | 0,015 | Сталь закаленная по стали (шариковый подшипник) | 0,001 |
| 2. | Сталь по чугуну | 0,30 | Мягкая сталь по стали (колесо по рельсу) | 0,005 |
| 3. | Мягкая сталь по чугуну | 0,20 | ||
| 4. | Сталь по бронзе | 0,15 | ||
| 5. | Мягкая сталь по бронзе | 0,80 | ||
| 6. | Дерево по дереву | 0,40- 0,60 | Дерево по дереву | 0,05- 0,08 |
Окончательно получаем, что при качении без скольжения тяга S должна удовлетворять условиям
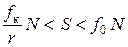 .
.
Откуда видно, что привести каток в качение значительно легче, чем привести его в скольжение. Этим объясняется то, что в технике, когда это возможно, стремятся заменить скольжение качением (колеса, катка, шариковые подшипники и т.п.).
Итак, реакция опорной поверхности при качении тела без скольжения состоит из:
1) нормальной реакции 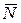 ;
;
2) силы трения 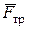 , препятствующей скольжению;
, препятствующей скольжению;
3) пары трения качения с моментом 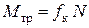 , препятствующей вращению тела.
, препятствующей вращению тела.
Найдем работу названных сил и пары.
Так как при качении без скольжения скорость точки касания тела с опорой равна нулю ( 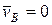 ), то
), то
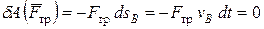 ,
, 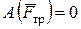 .
.
Очевидно, что
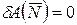 ,
, 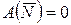
Далее, элементарная работа пары трения качения определяется формулой
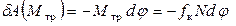 .
.
Или
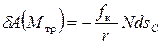 ,
,
где 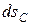 - элементарное перемещение центра С катка.
- элементарное перемещение центра С катка.
Полная работа пары трения качения определяется интегралом
 .
.
В случае 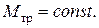 полная работа будет равна
полная работа будет равна
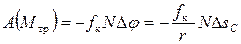 ,
,
где 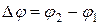 ,
, 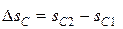 .
.
Задачи
Теорему об изменении кинетической энергии механической системы целесообразно применять к решению задач, в которых рассматривается движение механической системы с одной степенью свободы, а реакции наложенных на нее связей не совершают работу.
С помощью теоремы об изменении кинетической энергии в интегральной форме легко решаются задачи на определение скоростей (линейных и угловых), когда известны перемещения и действующие силы (они должны быть постоянными или зависящими только от перемещений).
Дифференциальная форма теоремы об изменении кинетической энергии применяется для определения ускорений (линейных или угловых),а также для составления дифференциального уравнения движения механической системы.
Если механическая система состоит из абсолютно твёрдых тел, соединенных нерастяжимыми нитями и шарнирами, причем трение сочлененных тел не учитывается, то для такой системы достаточно изобразить только внешние силы, так как работа внутренних сил в этом случае будет равна нулю
Дата добавления: 2019-04-03; просмотров: 444;
