Таким образом, вес арифметической средины в n раз больше веса отдельного измерения.

Так как вес отдельного измеренияр = 1, то вес арифметической средины Р = n. Следовательно, вес арифметической средины равен числу измерений, из которых она составлена.

Б) Оценка точности отдельного измерения и среднего

Арифметического

Оценка точности результатов неравноточных измерений заключается в определении вероятнейшего значения весового арифметического среднего L_о ,средней квадратической ошибки отдельного результата измерения 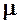, вес которого равен1,исредней квадратической ошибки М _оарифметической средины.

При этом значение арифметической средины рассчитывается из соотношения

L_o = 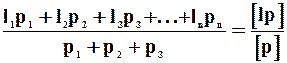.( 41 )

Среднюю квадратическую ошибку отдельного результата измерения, вес которого равен единице, называют ср.кв.ош. единицы веса.

Если известны истинные случайные ошибки измерений 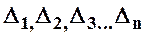, то ср.кв.ош. единицы веса определяют по формуле

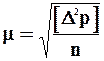. ( 42 )

Если истинные ошибки неизвестны, то оценку точности выполняют по вероятнейшим уклонениям из выражения

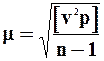.( 43 )

Среднюю квадратическую ошибку арифметической средины М_о вычисляют по формуле

М ₀ = 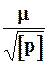.( 44 )

Вопросы для контроля

1 Классификация измерений и ошибок измерений

2 Свойства случайных ошибок

3 Понятие равноточных измерений. Оценка точности по формуле Гаусса

4 Оценка точности измерений по формуле Бесселя

5 Оценка точности измерений по разностям двойных измерений

6 Понятие относительной ошибки

7 Понятие неравноточных измерений, арифметической средины

8 Оценка точности отдельного результата неравноточного измерения

9 Оценка точности арифметической средины по результатам неравноточных измерений

10 Последовательность оценки точности равноточных измерений