Схема выбора с возвращением
Если при выборке r элементов из n элементы возвращаются обратно и упорядочиваются, то говорят, что это размещения с повторениями.
Размещения с повторениями могут отличаться друг от друга элементами, их порядком и количеством повторений элементов. Число всех размещений из n элементов по r с повторениями обозначается символом 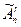 и вычисляется по формуле:
и вычисляется по формуле:
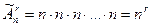 . .
| (2.10) |
Пример 2.6. Из множества 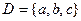 составить все размещения по 2 элемента с повторениями.
составить все размещения по 2 элемента с повторениями.
Решение:
По формуле (2.10) число размещений по два с повторениями равно
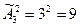 .
.
Это: (a, a), (a, b), (a, c), (b, a), (b, b), (b, c), (c, a), (c, b), (c, c).
Если при выборке r элементов из n элементы возвращаются обратно без последующего упорядочивания, то говорят, что это сочетания с повторениями.
Число всех сочетаний из n элементов по m с повторениями обозначается символом 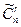 и вычисляется по формуле:
и вычисляется по формуле:
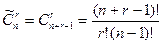 . .
| (2.11) |
Пример 2.7. Сколькими способами можно составить букет из 5 цветов, если в наличии есть цветы трех сортов?
Решение:
Рассматриваемое множество состоит из трех различных элементов, а выборки имеют объем равный 5. Поскольку порядок расположения цветов в букете не играет роли, то искомое число букетов равно числу сочетаний с повторениями из трех элементов по 5 в каждом. По формуле (2.11) имеем
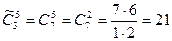 .
.
Перестановки из n элементов данного множества называются перестановками с повторениями из n элементов обозначается символом 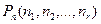 и вычисляются по формуле:
и вычисляются по формуле:
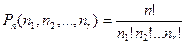 . .
| (2.12) |
Пример 2.8. Найти число различных слов, которое можно получить, переставляя буквы слова «математика».
Решение:
Разные буквы слова «математика» представляют собой множества Al, A2, ..., Ak, на которые можно разбить исходное слово и различные объединения которых будут давать новые бессмысленные слова. Здесь 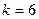 ,
, 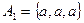 ,
, 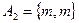 ,
, 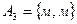 ,
, 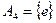 ,
, 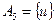 ,
, 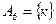 . Отсюда
. Отсюда 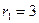 ,
, 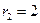 ,
, 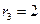 ,
, 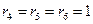 . Исходное множество
. Исходное множество 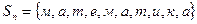 ,
, 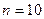 . Тогда по формуле (2.12)
. Тогда по формуле (2.12)
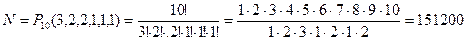 .
.
Дата добавления: 2017-03-29; просмотров: 281;
