Схема выбора без возвращений

Пусть дано множество, состоящее из n различных элементов.

Размещением из n элементов по r элементов (0< r ≤ n) называется любое упорядоченное подмножество данного множества, содержащее r элементов.

Из определения вытекает, что размещения – это выборки, состоящие из r элементов, которые отличаются друг от друга либо составом элементов, либо порядком их расположения. Число размещений из n элементов по r элементов обозначается символом 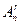и вычисляется по формуле:

,

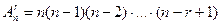(2.1)

или

,

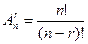(2.2)

где , ,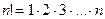

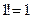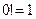
Для составления размещения 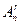надо выбрать r элементов из множества с n элементами и упорядочить их, т.е. заполнить r мест элементами множества. Первый элемент можно выбрать n способами, т.е. на первое место можно поместить любой из n элементов. После этого второй элемент можно выбрать из оставшихся n-1 элементов n-1 способами. Для выбора третьего элемента имеется n-2 способа, четвертого - n-3 способа, и наконец, для последнего r-го элемента - (n-(r-1)) способов. Таким образом, по правилу умножения, существует n(n-1)( n-2) ... (n-(r-1)) способов выбора r элементов из данных n элементов, т.е. .

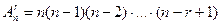Пример 2.3. Составить различные размещения по 2 элемента из множества 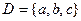и подсчитать их число.

Решение:

Из трех элементов можно образовать следующие размещения по два элемента:

(a, b), (a, c), (b, a), (c, a), (b, c), (c, b).

Согласно формуле (2.2) их число

.

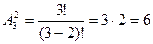Перестановкой из n элементов называется размещение из n элементов по n элементов.

Из определения вытекает, что перестановки – это выборки, состоящие из n элементов и отличающиеся друг от друга только порядком следования элементов. Число перестановок из n элементов обозначается символом Р_n и вычисляется по формуле:

Формула следует из определения перестановки:

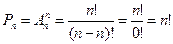
(2.4)

Пример 2.4. Сколько различных перестановок можно составить из элементов множества ?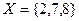

Решение:

Из элементов данного множества можно составить следующие перестановки:

(2, 7, 8), (2, 8, 7), (7, 2, 8), (7, 8, 2), (8, 2, 7), (8, 7, 2).

По формуле (2.3) имеем

.

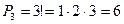Сочетанием из n элементов по r (0 ≤ r ≤ n) элементов называется любое подмножество, которое содержит r элементов данного множества.

Из определения вытекает, что сочетания – это выборки, каждая из которых состоит из r элементов, взятых из данных n элементов, которые отличаются друг от друга хотя бы одним элементом.

Число сочетаний из n элементов по r элементов обозначается символом и вычисляется по формуле:

.

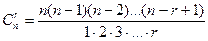(2.5)

или

.

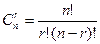(2.6)

Число 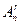размещений из n элементов по r элементов можно найти следующим образом: выбрать r элементов из множества, содержащего n элементов, затем в каждом из полученных сочетаний сделать все перестановки для упорядочивания подмножеств. Следовательно, согласно правилу умножения можно записать: 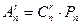, Отсюда 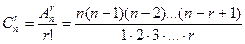или .

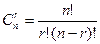Можно показать, что имеют место формулы:

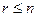, ( ),	(2.7)
,	(2.8)
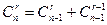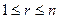( ).	(2.9)

Пример 2.5.Сколькими способами можно выбрать 3 цветка из вазы, в которой стоят 10 красных и 4 розовых гвоздики? Если выбрать 1 красную и 2 розовых гвоздики?

Решение:

Так как порядок выбора цветов не имеет значения, то выбрать 3 цветка из вазы, в которой стоят 14 гвоздик, можно 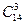способами. По формуле (2.6) находим, что

.

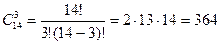Красную гвоздику можно выбрать 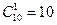способами. Выбрать две розовые из четырех имеющихся можно 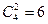способами. По правилу произведения букет из одной красной и двух розовых гвоздик можно составить 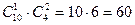способами.