Долгота - угол между плоскостью экватора и отвесной линией в данной точке (п. 1.3.4).

2. Широта - угол между плоскостью экватора и отвесной линией данной точки.

Долгота - угол между плоскостями начального меридиана и астрономического меридиана в данной точке (п. 1.3.5).

Ответ 1.3.4. Вы невнимательно читали п.1.3.1.

Вернитесь к нему и затем ­выберите правильный ответ.

Ответ 1.2.5. Правильно.

Переходите к следующему вопросы.

ВОПРОС. Как изменяется широта и долгота точки, если точка перемещается по поверхности Земли по меридиану от полюса к экватору?

1. Широта и долгота растут (п. 1.3.6)

2. Широта и долгота убывают (п. 1.3.7)

3. Широта убывает, долгота остается неизменной (п. 1.3.8).

Ответ 1.3.9. Неправильно. Прочитайте еще раз п.1.3.1. и выберите правиль­ный ответ.

Ответ 1.3.7. Так же неправильно. Вернитесь к п.1.3.1 и затем выберите правильный ответ.

Ответ 1.3.8. Верно.

Переходите к изучению п.1.3.9.

1.3.9. Геодезическая система координат.

Положение точки на земной поверхности так же определяется широ­той и долготой. Эти координаты получают вычислением на эллипсоиде по результатам геодезических измерений. Геодезической широтой «В» будет угол, образованный нормалью в точке к поверхности эллипсоида с плос­костью экватора; геодезической долготой «L» будет двугранный угол между плоскостями начального меридиана и плоскостью геодезического меридиана данной точки, проходящей через нормаль и полюсы эллипсоида.

Геодезические координаты не равны астрономическим, так как первые связаны с нормалями поверхности эллипсоида, а вторые с отвесными линими, то есть с нормалями к поверхности геоида.

ВОПРОС. Чем отличается геодезические координаты точки от астрономи­ческих?

1. Геодезические координаты получают вычислением, а астрономичес­кие из наблюдений (п. 1.3.10).

2. Геодезические и астрономические координаты считают между раз­личными направлениями и плоскостями (п. 1.3.11).

Ответ 1.3.10. Это так, но существенное отличие не в этом, прочтите еще раз п.п. 1.3.1 и 1.3.9 и выберите правильный ответ.

Ответ 1.3.11. Совершенно верно. При отсчитывании астрономических координат j и l фигурируют отвесная линия и плоскость астрономического ме­ридиана, а при от считывании геодезических координат «В» и «L» - нормаль к поверхности эллипсоида и плоскость геодезического меридиана.

Пере­ходите к изучению п.1.3.12.

1.3.12. Зональные плоские прямоугольные координаты Гаусса - Крюгера.

Для получения системы плоских прямоугольных координат Гаусса-Крюгера земной эллипсоид меридианами разбивают на шести- или трехградусные зоны по долготе. Нумерация зон проводится с запада на восток от Гринвичского меридиана. 1. Центральный меридиан зоны изображается на плоскости пряной, без искажения длины, т.е. масштаб на этой прямой равен единице. Эта прямая называется осевым меридианом зоны.

2. Экватор изображается также прямой, перпендикулярной осевому меридиану

3. Прочие меридианы и параллели изображаются кривыми взаимно пер­пендикулярными, т.е. нa проекции сохраняются углы, имеющиеся между мери­дианами и параллелями на поверхности эллипсоида,

4. Осевой меридиан плоской зоны принимают за ось X, изображение экватора за ось У (рис.1.3).

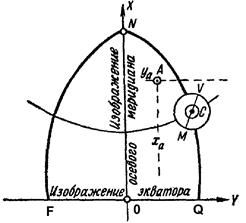
Рис.1.3. Зональные прямоугольные координаты Гаусса-Крюгера

Началом координат будет точка пересечения осевого меридиана с изображением экватора. На север от зкватора направление оси X положительно, на юг - отрицательное. На восток от оси X значения У считают положительными, на запад - отрицательными. Чтобы не иметь дела с отрицательными ординатами, ординату среднего меридиана считают за + 500 км, т.е. начало координат перенесено на запад на 500 км. Указанная система прямоугольных координат распространяется на площадь шести- или трехградусной зоны.

ВОПРОС. Какие линии зоны приняты за оси зональной прямоугольной системы коор­динат?

1. Линии меридиана и параллели (п. 1.3.13).

2. Линии меридиана и экватора (п. 1.3.14).

3. Линии среднего (осевого) меридиана и экватора (п. 1.8.15).

Ответ 1.3.13. Вы поспешили с выборок ответа. Вернитесь к п.1.3.12 и выберите правильный ответ.

Ответ 1.3.14. Неправильно. Прочтите еще раз внимательно п.1.3.12 и выбери­те правильный ответ.

Ответ 1.3.15. Вы правы.