Математические модели поверхности Земли, применяемые в геодезии

1. Если бы Земля была бы однородной, неподвижной и подвержена только действию внутренних сил тяготения, она имела бы форму шара(рис.1.2).

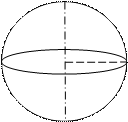Рис. 1.2. Шар

2. Под действием центробежной силы, вызванной вращением вокруг оси с постоянной скоростью, Земля приобрела форму сфероида или эллипсоида вращения(рис.1.3).

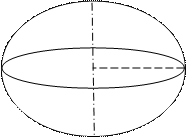Рис. 1.3. Эллипсоид вращения

3. На самом деле, из-за неравномерного распределения масс внутри Земли, эллипсоидальная фигура Земли сдеформирована и имеет форму геоида (рис.1.4). Наибольшие отступления геоида от эллипсоида не превышают 100 – 150 м.

Т.о. специальными инструментами с физической поверхности Земли геодезические измерения проектируют на геоид, фигура которого не изучена. Фигуру геоида заменяют правильной математической фигурой, к которой можно применять математические законы. Размеры земного эллипсоида составляют:

большая полуось а = 6378245 м,

малая полуось b = 6356863 м,

полярное сжатие a = 1: 298,3.

Рис. 1.4. Геоид

4. Для того, чтобы земной эллипсоид ближе подходил к геоиду, его располагают в теле Земли, ориентируя определенным образом. Такой эллипсоид с определенными параметрами и определенным образом ориентированный в теле Земли, называется референц-эллипсоидом (рис.1.5).

Рис. 1.5. Референц-эллипсоид

5. Геоид не может быть строго изучен из-за незнания распределения плотности масс внутри Земли. Было предложено вместо геоида принять фигуру квазигеоида (рис.1.6), которая может быть определена точно на основании астрономо-геодезических и гравиметрических измерений на поверхности Земли без учета внутреннего строения и плотности масс внутри Земли. Поверхность квазигеоидаотклоняется от поверхности геоида максимально 2 м в горных районах, на океанах и морях их поверхности совпадают.

Рис. 1.6. Квазигеоид