Построение математической модели задачи.

Модель должна объединить необходимое и достаточное количество формально описанных характеристик и условий, чтобы адекватно отражать физическую и экономическую сущность явлений.

Однако учет всех факторов в реальных задачах может включать громоздкие и сложные модели, решение которых существующими методами невозможно.

При составлении математической модели необходимо стремиться к ее упрощению, следует выделять главные решающие факторы.

В соответствии с постановкой задачи записывают ее целевую функцию и условия оптимизации плана распределения парка машин.

Если в качестве критерия оптимальности принят суммарный размер себестоимости или трудоемкости работ, то целевая функция имеет вид суммы соответствующих затрат на производство работ всеми машинами на всех участках или объектах

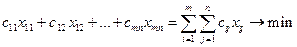
где с_ij – себестоимость работ за 1 маш.-ч. работы комплекта машин i – го типа на j – м участке, руб.;

x_ij – число затраченных машино-часов.

Решение задачи сводится к определению величин x_ij , при которых достигается минимум суммарной себестоимости работ.

Условия выполнения полного объема работ V_i на каждом производственном участке записывают в виде уравнения

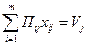; j = 1,2,…n

где П_ij – производительность комплекта машин i – го типа на j – м участке;

V_j – объем работ на j – м участке.

В левой части равенства – суммарная выработка машин на j – м участке, в правой части – объем работ на j – м участке. Суммарная выработка машин должна обеспечивать выполнение объема работ на этом участке.

Условия своевременного выполнения механизированных работ ресурсами данного парка машин записывают в виде ограничений на затраты времени каждой машины в планируемом периоде. Ограничения имеют вид неравенства

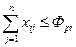; i = 1,2,…,m

В левой части неравенства записана сумма машино-часов работы машин i – го типа на производственных участках. В правой части, Ф_pi – фонд рабочего времени машин i – го типа.

Следовательно, на каких бы производственных участках ни планировалась работа машин i – го типа, суммарные затраты машино-часов не должны превышать фонд рабочего времени, которым располагают эти машины в течение планируемого периода.

Затраты машино-часов не могут быть отрицательными. Поэтому можно записать неравенство

x_ij ≥ 0 ; i = 1,2,…,m ; j = 1,2,…,n.

Целевая функция

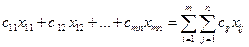
и условия

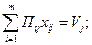j = 1,2,…,n

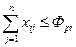; i = 1,2,…,m

x_ij ≥ 0 ; i = 1,2,…,m ; j = 1,2,…,n.

составляют математическую модель распределительной задачи линейного программирования. Для ее решения вначале находят допустимый (исходный) рациональный вариант расстановки машин, который затем последовательно улучшают до оптимума.

Разработка исходного варианта распределения парка машин.

Исходные данные для решения задачи записывают в виде расчетной таблицы 1. В верхней части таблицы указывают номера объектов или производственных участков (j = 1,…,n) и объем работ на каждом объекте V_n.

Слева записывают типоразмеры и число машин; каждая строка соответствует машинам i – го типоразмера и нумеруется ( i = 1,…,n).

Справа помещается графа “Фонд рабочего времени” ведущих машин Ф_i и графа “Резерв”.

В каждой ij – й клетке таблицы записывают:

Справа вверху – плановую себестоимость С_ij механизированных работ на j – м участке, отнесенные к единице машиноресурсов i – го типоразмера;

Справа внизу – плановую эксплуатационную производительность П_ij ведущей машины i – го типа в единицах конечной продукции на j – м участке;

Таблица 1 – Матрица исходных данных

Типорамер машин	Порядковый номер	Участок	Фонд Ф, маш.-ч	Резерв, маш.-ч
		…	n
Объем работы, тыс.м³
V₁	V₂	…	V_n
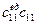		х₁₁П₁₁	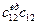х₁₂П₁₂	…	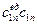х_1nП_1n	Ф₁
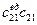		х₂₁П₂₁	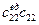х₂₂П₂₂	…	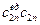х_2nП_2n	Ф₂
…	…	…	…	…	…	…
	m	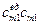х_m₁П_m₁	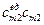х_m₂П_m₂		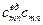х_mnП_mn	Ф_m

Ф_i – фонд рабочего времени ведущих машин, маш.-ч;

C_ij – плановая себестоимость механизированных работ за 1 маш.-ч на j – м участке комплекта машин i – го типа, руб.;

П_ij – производительность машины i – го типа на j – м участке в натуральных измерениях;

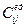– удельная себестоимость единицы продукции машины i – го типоразмера на j – м участке;

x_ij – затраты машиноресурсов, маш.-ч.

Слева вверху – удельную себестоимость 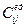в руб. на единицу продукции машины i – го типоразмера на j – м участке;

Слева внизу – оставляют место для затрат машиноресурсов x_ij , которые определяют в результате решения задач.

Среди всех величин себестоимости 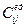находят наименьшую.

В соответствующую ij – ю клетку таблицы записывают количество машиноресурсов машин i – го типа, не превышающее фондов Ф_i и их потребности для выполнения объема работ на j – м участке.

Искомое количество машиноресурсов

x_ij = min (Ф_i; V_j / П_ij)

Если для выполнения работ на j – м участке требуется затратить количество машиноресурсов i – го типа машин, превышающее фонд Ф_i , то x_ij принимают равным Ф_i и в дальнейших расчетах по составлению приближенного плана машины i – го типа не рассматривают.

Объем работ на j – м участке принимают равным V_i – П_ij x_ij .

Если же для выполнения работ на j – м участке требуются затраты машино-часов x_ij < Ф_i , то в дальнейших расчетах j – й участок не рассматривают, а фонд рабочего времени машин i – го типа принимают равным Ф_i – x_ij .

Для заполнения следующей позиции табл. 1 вновь находят наименьшую величину 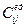, исключая уже рассмотренную. Расчеты проводят до тех пор, пока не будет обеспечено выполнение объемов работ на всех участках.

Заполненная таблица представляет собой рациональный план распределения фондов рабочего времени машин.

По этому плану возможны остатки рабочего времени (машиноресурсов), которые записывают в графе “резерв”.

Если с помощью описанного вычислительного процесса не удается составить допустимый план, обеспечивающий выполнение работ на всех участках, то машины следует расставить по тем участкам, где они дают наибольшую выработку.

Если и в этом случае план не является допустимым, то следовательно, ресурсами парка машин нельзя своевременно выполнить заданный объем работ.

Если на отдельных участках или объемах срок производства работ ограничен, то в дополнение к записанной ранее модели записывают неравенство

x_ij ≤ d_ij,

где d_ij – ограничение, определяемое выражением

d_ij = T_j t_i R_i ,

где T_j – заданный срок производства работ на j – м участке, дн.;

t_i – число часов работы ведущей машины в день;

R_i – число ведущих машин в комплекте.

Расчет машиноресурсов выполняют по формуле

x_ij = min (Ф_i, d_ij, V_i / П_ij)

Позиции таблицы заполняют до тех пор, пока не будет обеспечено выполнение всех объемов работ.

Если окажется, что фондов рабочего времени машин недостаточно, то задачу решают по критерию наибольшей выработки машин. При этом в таблице находят позицию с наибольшей выработкой П_ij и в нее записывают x_ij , определяемый по формуле

x_ij = V_i / П_ij

Дата добавления: 2017-03-29; просмотров: 114;