Количественные характеристики систем массового обслуживания.
Количественные характеристики систем массового обслуживанияявляются:
– число требований (объектов обслуживания), находящихся в очереди Y;
– время ожидания в очереди до начала обслуживания tf ;
– математическое ожидание числа требований в системе m, т. е. в очереди и обслуживании.
При решении многих практических задач достаточно знать средние значения этих величин Ỹ и ŧf .
Характеристики Ỹ и ŧf зависят от коэффициента использования системы (т.е. показателя интенсивности обслуживания)
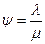 ,
,
где λ – средняя интенсивность потока требований на обслуживание;
μ – возможная интенсивность обслуживания, определяемая пропускной способностью прибора обслуживания.
В теории массового обслуживания рассматриваются задачи, когда ψ < 1,0 , т.е. пропускная способность канала обслуживания больше, чем средняя интенсивность потока требований на обслуживание.
При ψ > 1,0 становится очевидным, что в единицу времени к которой относятся показатели λ и μ , останутся не обслуженными λ – μ требований и очередь будет расти пропорционально времени.
Математическое ожидание m’ находится из соотношения
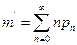
где pn – вероятность того, что в системе находится n требований.
Средняя длительность обслуживания определяется по формуле
ŧ0 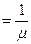
Среднее время пребывания требования в системе ŧs определяется из соотношения
ŧs = ŧf + ŧ0
где ŧf – время ожидания в очереди
ŧ0 – время обслуживания
Среднее количество требований , находящихся в очереди, равно математическому ожиданию числа требований в системе минус математическое ожидание количества требований, находящихся в обслуживании:
Ỹ = m’ – ψ
Время ожидания в очереди
ŧf 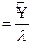
Основной задачей является получение формулы для установления величины pn . Вероятности того, что в системе находится n требований.
Тогда последовательно могут быть вычислены количественные характеристики полностью определяющие работу системы массового обслуживания: m’ – математическое ожидание; Ỹ – среднее число требований, находящееся в очереди; ŧf – время ожидания в очереди; ŧs – время пребывания требований в системе.
Определение вероятности pn является сложной задачей.
Наиболее просто pn находится в тех случаях, когда поток заявок на обслуживание удовлетворяет условиям стационарности, отсутствия последействия и ординарности.
Свойство стационарности заключается в том, что вероятность поступления определенного числа требований в течение заданного промежутка времени не зависит от начала отсчета времени, а зависит лишь от длинны этого промежутка.
Отсутствие последствия характеризуется тем, что число требований, поступивших в систему после какого-либо момента времени, не зависит от числа требований, поступивших до этого времени.
Ординарными являются потоки, для которых вероятность появления более одного требования за малый промежуток времени бесконечно мала по сравнению с длиной этого промежутка.
Поток заявок на обслуживание, удовлетворяющий 3 – м названным условиям называется пуассоновским и выражается распределением вероятностей
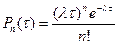
где Pn (τ) – вероятность поступления за время τ заявок на обслуживание;
е – основание натуральных логарифмов (е = 2,7183)
n – число требований находящихся в системе.
Такие системы описываются с помощью системы обыкновенных дифференциальных уравнений.
При решении конкретных задач методом ТМО необходима проверка гипотезы о том, что поток заявок на обслуживание является пуассоновским.
Решение технико-экономических задач с использованием теории массового обслуживания включает следующие этапы:
а) статистическое изучение требований , поступающих в систему; определение интенсивности и закона распределения входящего потока;
б) изучение структуры реальной системы, порядка и времени обслуживания поступающих в нее требований, определение на этой основе типа системы массового обслуживания и установление критериев для оценки качества ее функционирования;
в) выбор метода решения задачи и определение вероятностных характеристик и критериев эффективности функционирования системы;
г) технико-экономическая оценка результатов решений и выбор оптимального варианта функционирования системы.
При статистическом изучении потока требований выделяются простейшие потоки, имеющие пуассоновское распределение, а для времени обслуживания – показательный закон распределения, имеющий вид
F(τ) = 1 – e–μτ
где μ – параметр показательного закона, характеризующий пропускную способность или среднюю производительность системы обслуживания.
Величина (1/μ) – среднее время обслуживания 1 – го требования.
Соответствие статистических данных о потоке требований и времени обслуживания указанным законам распределения устанавливается следующим образом:
– вычисляются среднее значение числа требований, поступающих в систему за принятую единицу времени (λ) , и средняя продолжительность их обслуживания (1/μ);
– найденные значения λ и μ подставляются соответственно в уравнения
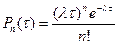
и
F(τ) = 1 – e–μτ
по которым определяются теоретические распределения потока требований и времени обслуживания;
На основании статистического и теоретического распределений определяется степень согласованности их между собой используя критерий Х2
Х2 = 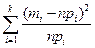
где mi – число значений (требований) в i – м разряде;
k – число разрядов;
n – общее число наблюдений;
pi – теоретическая вероятность i – го разряда.
Если статистическое распределение потока требований и времени обслуживания согласуются с указанными теоретическими, то расчет критериев эффективности функционирования системы может осуществляться с помощью аналитических методов.
Формирование комплекта машин для земляных работ с использованием теории массового обслуживания.
Расчетные характеристики разомкнутой системы массового обслуживания Завадскас Э.К. Выбор рациональных вариантов комплексной механизации.
Производство земляных работ является одним из наиболее механизированных участков строительного производства. При выполнении земляных работ используются различные строительные машины и транспортные средства, отличающиеся с одной стороны, высокой производительностью, с другой стороны – относительно большой стоимостью, потреблением большого количества ГСМ. Этим обуславливается необходимость изыскания рациональной технологии и организации выполнения земляных работ в целях обеспечения экономичного использования технических средств.
Решение задачи оптимизации технологии производства земляных работ включает определение оптимального числа транспортных средств, перевозящих выкопанный грунт и прикрепленных к соответствующим погрузочным средствам.
Суть методики определения оптимального количества транспортных средств, обеспечивающих минимальные потери от простоя транспортных средств и средств погрузки.
Суммарные потери S от простоя транспортных Sт и погрузочных средств Sп в целом за смену
S = Sп + Sт ;
Sп = Pоп Sоп ;
Sт = 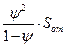
где S – суммарные потери от простоя транспортных и погрузочных средств в целом за смену;
Sп, Sт – соответственно, потери от простоя погрузочных средств (экскаватора) и транспортных средств (автомобилей – самосвалов);
Sоп, Sот – соответственно, стоимость работы погрузочных и транспортных средств за одну смену;
Pоп – вероятность простоя экскаватора;
ψ – коэффициент использования системы массового обслуживания, в которой транспортные средства предъявляют заявки (требования) экскаватору на соответствующее обслуживание.
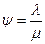
где λ – средняя интенсивность потока требований на обслуживание (потоки поступающих к экскаватору автомобилей – самосвалов);
μ – интенсивность обслуживания автомобилей – самосвалов экскаватором.
Суммарные потери от простоя транспортных и погрузочных средств определяются уравнением
S = 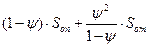 (1)
(1)
С помощью уравнения (1) находится оптимальное значение коэффициента (показателя интенсивности обслуживаний)
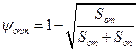
Оптимальное количество транспортных средств, прикрепленных к экскаватору
nопт = tp μ ψопт (2)
где tp – продолжительность одно рейса автомобиля – самосвала;
μ – интенсивность обслуживания самосвалов экскаватором.
Формула (2) определения количества транспортных средств используется тогда, когда при производстве земляных работ ощущается нехватка самосвалов и достаточное количество погрузочных средств.
Если лимитирующим фактором является наличие погрузочных средств при ненапряженной работе транспорта, можно исходить из предположения полной загрузки самосвалов и игнорировать соотношение между стоимостью одной смены. Это не обеспечивает получения строго оптимального решения, однако позволяет пользоваться упрощенной формулой расчета количества транспортных средств
n = tp μ при ψ = 1
n = tp μ kэ при ψ < 1
где kэ – коэффициент использования времени экскаватора;
tp – продолжительность одного рейса, ч.
Продолжительность одного рейса самосвала определяется по формуле
tp = t1 + t2 + t3 + t4
при этом
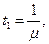
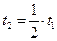
где t1, t2, t3 – соответственно, продолжительность погрузки, выгрузки, движения;
t4 – среднее время ожидания в очереди;
при этом t4 = 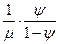
Дата добавления: 2017-03-29; просмотров: 571;
