Теория дискретных систем автоматики и телемеханики 1 страница
Теория дискретных систем (ТДУ) является сравнительно молодым, но активно развивающимся разделом науки. Ее появление относится к 30-м годам прошлого века и было продиктовано усложнением и совершенствованием релейных систем управления и возникновением острой необходимости в их строгом математическом описании. Новым толчком в развитии ТДУ в 50-х годах прошлого века послужило активное внедрение в различных устройствах управления полупроводниковой техники и в качестве компонентов систем управления всевозможными технологическими процессами – цифровых вычислительных машин. В конце прошлого и с начала 21-го века чрезвычайно актуальными стали проблемы разработки ТДУ, обусловленные активным применением в системах управления микросхем большой степени интеграции, программируемых логических матриц (ПЛМ), микропроцессоров и т.п.
Основы ТДУ начали закладываться в конце 30-х – начале 40-х годов прошлого века в работах ряда ученых, обнаруживших и доказавших возможность применения чисто математической дисциплины, булевой алгебры, при анализе и синтезе так называемых контактных схем. К числу этих ученых принадлежали сотрудник МГУ В.И. Шестаков, американец К. Шеннон и японец Накашима. Применение аппарата математической логики для решения задач, возникающих при синтезе дискретной техники, активно развивалось в трудах советских ученых В.М. Глушкова, М.А. Гаврилова, Д.А. Поспелова, В.Г. Лазарева, А.Д. Закревского и ряда других.
Устройства железнодорожной автоматики, телемеханики и связи (ЖАТС) в основном относятся к классу дискретных устройств (ДУ). Так, на железных дорогах работает большое число дискретных систем электрической централизации, автоматической блокировки, диспетчерской централизации, систем горочной автоматики и т.п. Большинство таких систем выполняет ответственные функции и эксплуатируется в очень тяжелых режимах. Вследствие этого к таким системам предъявляют жесткие требования по надежности, безопасности и устойчивости работы.
Все системы ЖАТС по существу выполняют переработку, передачу, воспроизведение, хранение и доставку информации, используемой для управления разного рода технологическими процессами. Вся информация, циркулирующая в системах ЖАТС, отображается в виде сигналов. В современных устройствах ЖАТС обычно используются электрические сигналы. Физически величины, представляющие собой такой сигнал, обычно реализуются в виде тока или напряжения. Любой сигнал представляет собой средство для перенесения информации в пространстве и во времени. Если сигнал может принимать только определенные дискретные значения (в системах ЖАТС это обычно 0 или 1), то его называют дискретным.
2.Дискретные элементы
Для физического представления информации в ДУ используются дискретные элементы, которые могут находиться в двух состояниях, обычно ассоциируемых с 0 и 1. Информация, циркулирующая в системах автоматики и телемеханики, представляется в виде кодовых слов произвольной длины, состоящих из символов 0 и 1. Упомянутые символы могут также интерпретироваться как цифры двоичной системы счисления.
Любое ДУ – это некоторый функциональный блок, представляющий собой совокупность дискретных элементов, соединенных надлежащим образом. Под дискретным элементом (ДЭ) понимают минимальную совокупность деталей, объединенных в общую схему для выполнения заданной функции, имеющей так называемую релейную характеристику. Последнее означает, что изменение входных сигналов ДЭ вызывает скачкообразное изменение его выходных сигналов. Заметим, что параметрами упомянутых сигналов могут быть амплитуда тока, напряжение, значение сопротивления, частота импульсов и т.п.
В общем случае любой ДЭ может быть представлен в виде ( 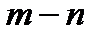 )-полюсника, где
)-полюсника, где 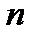 - число входов ДЭ, а
- число входов ДЭ, а 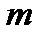 - число его выходов.
- число его выходов.
Все дискретные элементы делятся на комбинационные ДЭ и ДЭ с памятью. Комбинационные ДЭ характеризуются тем, что значения его выходов зависят только от значений его входов. В отличие от них значения выходов ДЭ с памятью зависят не только от значений входов, но и от состояний ДЭ, множество которых всегда конечно.
С точки зрения физического исполнения ДЭ делятся на контактные и бесконтактные.
Наиболее распространенными контактными ДЭ являются электромагнитные реле, подразделяющиеся на реле постоянного и переменного тока.
На представленном ниже рис. 1 представлен упрощенный вид конструкции реле постоянного тока. Оно состоит из сердечника с намотанной на него катушкой, при протекании по которой постоянного тока создается магнитный поток, который замыкается через якорь. При подаче напряжения на выводы катушки, она втягивает в себя сердечник по принципу электромагнита, при этом толкатель двигает (толкает) подвижную систему контактов, часть из которых при этом замыкается, а часть размыкается. Катушка воспринимает входной сигнал в виде тока или напряжения. Якорь является промежуточным звеном, который передает воздействие от воспринимающего органа к исполнительному. Последний представляет собой контактную систему, состоящую из группы контактов, одни из которых размыкают электрическую цепь (аналог сигнала 0), а другая замыкает (аналог сигнала 1).
На схемах ДУ для реле приняты обозначения, которые представлены на приведенном ниже рис. 2. На этом рисунке цифрами обозначены: 1- обмотка реле, 2- контакт замыкающий, 3- контакт размыкающий, 4- контакт замыкающий с замедлителем при срабатывании, 5- контакт замыкающий с замедлителем при возврате, 6 – контакт импульсный замыкающий, 7- контакт замыкающий без самовозврата, 8- контакт размыкающий без самовозврата, 9- контакт размыкающий с замедлением при срабатывании, 10 - контакт размыкающий с замедлением при возврате.
Несколько слов о бесконтактных ДЭ. Их действие основано на нелинейном изменении проводимости под влиянием напряжения тока или магнитного поля, воздействующих на элемент. Примерами таких ДЭ являются диоды и транзисторы. Современные бесконтактные ДЭ реализуются в виде интегральных схем (ИС) различной степени интеграции, в том числе больших ИС (БИС), сверхбольших (СБИС) и т.д., по технологии ТТЛ (транзисторно-транзисторной логики) или МОП (металл – окисел – проводник).
В заключение этого раздела приведем историческую справку.
Некоторые историки науки утверждают, что реле впервые было разработано и построено русским ученым П. Л. Шиллингом в 1830—1832 гг. Это реле составляло основную часть вызывного устройства в разработанном им телеграфе. Другие историки отдают первенство известному американскому физику Дж. Генри (его именем названа единица индуктивности — генри), который сконструировал контактное реле в 1835 году при попытках усовершенствовать изобретённый им в 1831 г. телеграфный аппарат и базировалось оно на электромагнитном принципе действия.
Слово реле возникло от французского relay — процедура смены уставших почтовых лошадей на станциях или передача эстафеты в спортивных эстафетных состязаниях. Как самостоятельное устройство реле впервые упомянуто в патенте на телеграф Самюэля Мора.

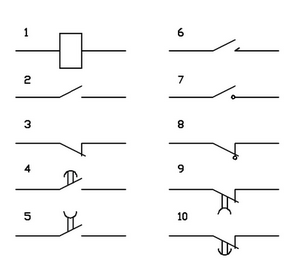
Рис.1 Рис.2
3. Системы счисления.
Любая информация, циркулирующая в ДУ, представляется в виде кодовых слов. Эти кодовые слова могут интерпретироваться как числа, представленные в некоторой системе счисления. Системы счисления (СС) представляют собой совокупность приемов и правил для записи чисел с использованием знаков, называемых цифрами.
В зависимости от способов изображения чисел цифрами все СС делятся на две группы – на непозиционные и позиционные.
Непозиционная СС – это система, в которой количественное значение (вес) каждой цифры не зависит от занимаемой ею позиции в изображении числа. Примером такой СС является широко известная римская СС. Так, в записи чисел IX и XI знак I – это символ цифры «единица». В первом числе единица вычитается из числа X, а во втором - прибавляется к нему. Таким образом, в обоих случаях цифра I имеет один и тот же «вес» и не зависит от того в какой позиции (слева или справа от цифры X) она находится.
Позиционная СС – это такая система, в которой вес каждой цифры зависит от позиции, которую она занимает в изображении числа. Количество знаков (символов), используемых для изображения чисел, называется основанием СС. Примером позиционной СС является десятичная (арабская) система, которой мы повсеместно пользуемся. Так, в записи чисел 311 и 13 знак цифры 3 первом числе означает три сотни, а во втором – три единицы. Таким образом цифра 3 имеет совершенно разный «вес» в этих числах, поскольку занимает в них разные позиции.
Не вдаваясь в детали отметим, что позиционные СС имеют ряд преимуществ перед непозиционными (относительная простота и удобство выполнения арифметических и логических операций, возможность просто представлять большие по значению числа, простота и естественность представления дробей и выполнения операций над ними). Поэтому в цифровой технике, оперирующей с дискретными величинами, используются именно позиционные СС.
Остановимся на них подробнее.
Любое 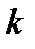 -разрядное целое число
-разрядное целое число 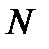 в позиционной СС с основанием
в позиционной СС с основанием 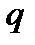 представляется в виде многочлена
представляется в виде многочлена
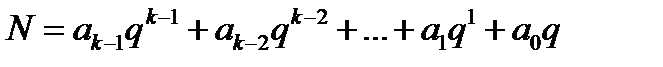 .
.
При 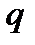 =16 мы имеем дело с 16-ричной СС, при
=16 мы имеем дело с 16-ричной СС, при 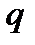 =10 - с десятичной СС, при
=10 - с десятичной СС, при 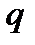 =8 - с восьмеричной, при
=8 - с восьмеричной, при 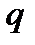 =2 - с двоичной.
=2 - с двоичной.
Цифры 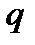 -ичной СС есть элементы множества
-ичной СС есть элементы множества 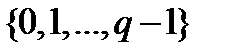 , содержащего
, содержащего 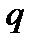 различных символов. Для 16-ричной СС это множество есть
различных символов. Для 16-ричной СС это множество есть 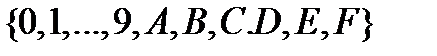 , где символ А обозначает «цифру» 10, В – «цифру» 11, С= 12,
, где символ А обозначает «цифру» 10, В – «цифру» 11, С= 12, 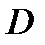 =13,
=13, 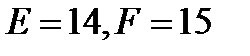 .
.
Каждая СС имеет свои правила арифметики, т.е. свои таблицы умножения и сложения. Производя какие-либо операции над числами, надо помнить о СС, в которой они представлены, и пользоваться соответствующими арифметическими правилами (таблицами).
Дискретные устройства (ДУ) автоматики и телемеханики - это устройства, использующие только два дискретных сигнала (0и1), и состоят они из элементов памяти, имеющих только два состояния (0 и 1). Поэтому, изучая цифровую технику, нам постоянно требуется иметь дело с двоичной СС. Большой интерес для нас будет представлять и восьмеричная СС. Перейдем теперь к преобразованиям целых чисел, представленных в произвольной 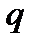 -ичной СС, в десятичную. Эта процедура для нас представляет большой интерес, поскольку мы имеем дело в большинстве случаев с вычислениями именно в десятичной системе счисления.
-ичной СС, в десятичную. Эта процедура для нас представляет большой интерес, поскольку мы имеем дело в большинстве случаев с вычислениями именно в десятичной системе счисления.
Процедура эта предельно проста. Записываем переводимое число в виде многочлена по степеням основания 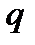 и по правилам десятичной арифметики выполняем соответствующие операции. Результатом является десятичный эквивалент исходного
и по правилам десятичной арифметики выполняем соответствующие операции. Результатом является десятичный эквивалент исходного  -ичного числа.
-ичного числа.
Условимся далее указывать основание 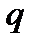 числа в виде соответствующего индекса этого числа.
числа в виде соответствующего индекса этого числа.
Рассмотрим примеры:
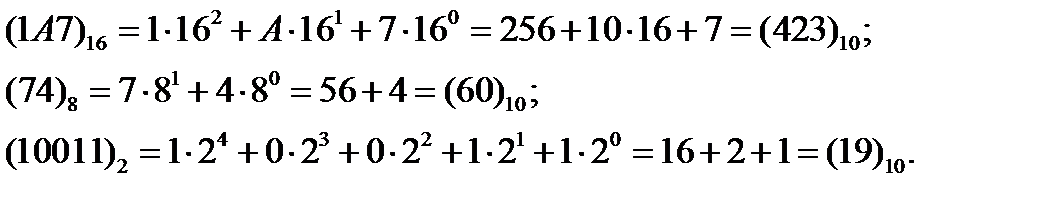
Опишем теперь три различных метода перевода чисел из десятичной системы в двоичную.
1). Метод вычитания.
Предварительно заготовим множество степеней двойки, в котором максимальная степень превосходит переводимое число 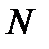 . Далее выбираем среди этих степеней такое число
. Далее выбираем среди этих степеней такое число 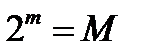 , которое является ближайшим к
, которое является ближайшим к 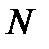 , но не превосходит его. Ясно, что у искомого двоичного числа в его представлении в виде двоичного многочлена максимальная степень двойки должна равняться
, но не превосходит его. Ясно, что у искомого двоичного числа в его представлении в виде двоичного многочлена максимальная степень двойки должна равняться 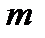 . Теперь вычисляем разность
. Теперь вычисляем разность 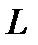 =
=  и для этого числа производим аналогичные действия. В результате определяется следующая степень
и для этого числа производим аналогичные действия. В результате определяется следующая степень 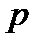 двойки, которая определяет второе слагаемое (вторую цифру) в искомом двоичном представлении числа
двойки, которая определяет второе слагаемое (вторую цифру) в искомом двоичном представлении числа 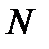 . Далее процесс продолжается аналогичным образом, а критерий окончания его очевиден.
. Далее процесс продолжается аналогичным образом, а критерий окончания его очевиден.
Проиллюстрируем метод на примере. Пусть требуется перевести число 97 в двоичную систему. Построим используемые степени двойки:
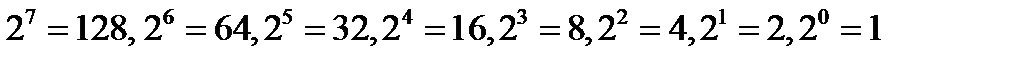 .
.
Ближайшее к 97 число из приведенной последовательности, но не превосходящее его, есть 64 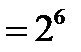 . Следовательно, в искомом двоичном числе цифра 6 будет старшей степенью двойки в искомом многочлене. Теперь вычисляем разность 97-64=33. Для числа 33 ближайшим, но не превосходящем его, есть число 32=
. Следовательно, в искомом двоичном числе цифра 6 будет старшей степенью двойки в искомом многочлене. Теперь вычисляем разность 97-64=33. Для числа 33 ближайшим, но не превосходящем его, есть число 32= 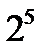 . Следовательно, следующее слагаемое в искомом многочлене есть
. Следовательно, следующее слагаемое в искомом многочлене есть 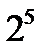 . Далее вычисляем разность 33-32=1. Поскольку 1=
. Далее вычисляем разность 33-32=1. Поскольку 1= 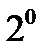 , то это будет очередное (и последнее) слагаемое в искомом двоичном многочлене. Итак, искомый результат таков:
, то это будет очередное (и последнее) слагаемое в искомом двоичном многочлене. Итак, искомый результат таков:
97= 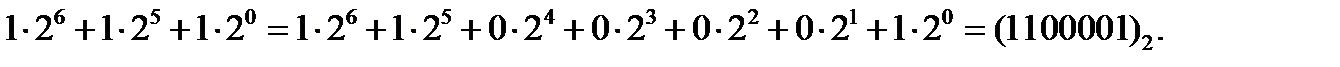
2).Метод деления.
Переводимое число делим на 2 и вычисляем остаток. Затем полученное частное вновь делим на 2 и находим остаток. Процесс продолжается далее аналогичным образом до тех пор, пока последнее частное не окажется равным 1. Теперь сформируем искомое двоичное число: его старшим разрядом будет последнее полученное частное, следующим за ним разрядом является последний остаток, последующий разряд – предыдущий остаток и т.д. Так происходит продвижение от последнего полученного частного к первому полученному остатку от деления исходного числа на 2. Выписанная в указанном порядке двоичная последовательность и есть искомый результат.
Проиллюстрируем это на нескольких примерах.
Заметим, что если последнее частное при выполнении процедуры деления равно 0, то искомое двоичное число будет начинаться с цифры 0. Понятно, что этот ноль целесообразно удалить из числа-результата, поскольку ноль в начале числа не влияет на его значение.
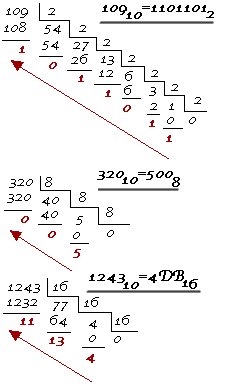
Легко доказать, что изложенный метод деления для перевода числа из десятичной СС в двоичную можно применять при переводе не только в двоичную, но и в СС с любым другим основанием, отличным от 2. При этом обращаем внимание, что все вычисления производятся по правилам десятичной арифметики. Ниже приведены три соответствующих примера перевода чисел в СС с основаниями 2,8 и 16.

3).Метод триад.
Он применим только для перевода чисел из десятичной системы в двоичную. Метод выполняется в два этапа. Сначала исходное десятичное число переводится в восьмеричную систему, затем каждая восьмеричная цифра полученного числа заменяется триадой – соответствующим этой цифре трехразрядным двоичным числом. Полученное в результате двоичное число представляет собой двоичный эквивалент исходного заданного десятичного числа. (Попробуйте в качестве упражнения получить точное математическое доказательство сформулированного утверждения).
Представление в виде двоичных триад каждой цифры восьмеричной системы можно получить методом деления на 2: 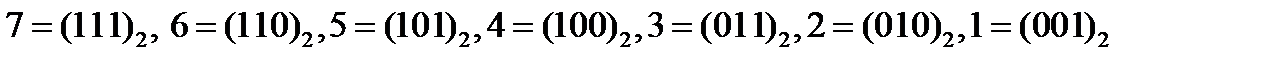 .
.
Рассмотрим примеры. Пусть задано число 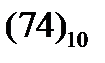 . Переведем его в восьмеричную СС любым из двух представленных выше методов и в результате получим число
. Переведем его в восьмеричную СС любым из двух представленных выше методов и в результате получим число 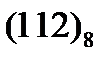 . В этом числе каждую цифру заменим соответствующей двоичной триадой:
. В этом числе каждую цифру заменим соответствующей двоичной триадой:  . Это и есть искомое двоичное число, в котором целесообразно отбросить два первых нуля, поскольку на его значение эти нули не влияют.
. Это и есть искомое двоичное число, в котором целесообразно отбросить два первых нуля, поскольку на его значение эти нули не влияют.
Еще один пример. Пусть задано десятичное число 97, переведем его в восьмеричную систему - 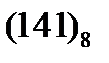 . Заменим каждую его цифру двоичной триадой –
. Заменим каждую его цифру двоичной триадой – 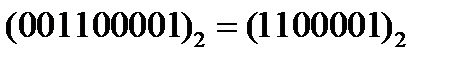 .
.
Это и есть искомый результат.
Сравнивая три изложенных метода перевода чисел ( 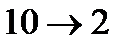 ) отметим, что метод триад является наиболее привлекательным как с точки зрения трудоемкости, так и компактности записей.
) отметим, что метод триад является наиболее привлекательным как с точки зрения трудоемкости, так и компактности записей.
Метод перевода делением 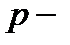 ичных чисел в
ичных чисел в 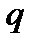 - ичные универсален в том смысле, что он годится для любых
- ичные универсален в том смысле, что он годится для любых 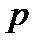 и
и 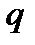 . Однако надо помнить, что при делении необходимо пользоваться правилами
. Однако надо помнить, что при делении необходимо пользоваться правилами  ичной арифметики. Очевидно, что при
ичной арифметики. Очевидно, что при 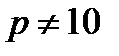 для нас это сопряжено с неудобствами, поскольку мы привыкли к вычислениям только в десятичной арифметике. В связи с этим можно предложить следующий простой прием, чтобы обойти это неудобство. Заданное
для нас это сопряжено с неудобствами, поскольку мы привыкли к вычислениям только в десятичной арифметике. В связи с этим можно предложить следующий простой прием, чтобы обойти это неудобство. Заданное 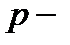 ичное число сначала переведем в десятичное число, затем по правилам десятичной арифметики методом деления на
ичное число сначала переведем в десятичное число, затем по правилам десятичной арифметики методом деления на 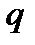 переведем его в
переведем его в 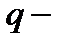 ичное число.
ичное число.
Рассмотрим пример. Пусть требуется число 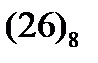 перевести, например, в троичную систему. Сначала переведем это число в десятичную СС: 2
перевести, например, в троичную систему. Сначала переведем это число в десятичную СС: 2  8+6
8+6 
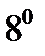 =22. Теперь, пользуясь правилами привычной для нас десятичной арифметики, методом деления на 3 переведем его в троичную систему:
=22. Теперь, пользуясь правилами привычной для нас десятичной арифметики, методом деления на 3 переведем его в троичную систему:  =
= 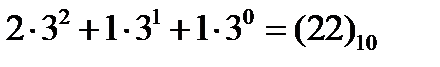 .
.
4. Функции алгебры логики.
Методы анализа и синтеза всех классов ДУ базируются на алгебре логики. Возникновение этого раздела математики связано с именем ирландца Дж. Буля (1815-1864). Важным понятием этого раздела является функция алгебры логики (ФАЛ). Переменные ФАЛ могут принимать одно из двух значений: True и False. В ТДУ эти значения традиционно обозначаются символами 1 и 0 cоответственно, но в теории ФАЛ они не интерпретируются как числа.
Функцию 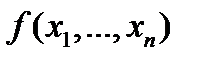 называют ФАЛ, если она, как и ее переменные, может принимать только два логических значения - 0 или 1. Другие названия ФАЛ: логическая, булева или переключательная функция. Переменные ФАЛ сопоставляют значениям сигналов на входах ДУ, а значение ФАЛ – со значением сигнала на его выходе.
называют ФАЛ, если она, как и ее переменные, может принимать только два логических значения - 0 или 1. Другие названия ФАЛ: логическая, булева или переключательная функция. Переменные ФАЛ сопоставляют значениям сигналов на входах ДУ, а значение ФАЛ – со значением сигнала на его выходе.
4.1. Способы представления ФАЛ.
Функции ФАЛ могут быть представлены различными способами:
1)Словесный способ. Здесь все случаи, при которых функция принимает значения 0 или 1, описываются словесно. Так, функцию «ИЛИ» со многими аргументами можно описать следующим образом: функция принимает значение 1, если хотя бы один из аргументов принимает значение 1, иначе значение функции равно 0.
2)Табличный способ. Булева функция задается в виде таблицы истинности. В левой части таблицы истинности записываются все возможные n-разрядные двоичные комбинации аргументов, а в последнем столбце – значения функции на этих наборах. Таблица истинности содержит 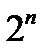 строк. Приведем пример задания ФАЛ
строк. Приведем пример задания ФАЛ 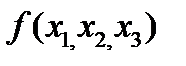 от трех переменных:
от трех переменных:
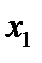
| 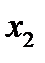
| 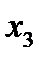
| 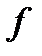
|
3) Числовой способ.Функция задается в виде последовательности десятичных эквивалентов тех наборов аргументов, на которых функция принимает значение 1. Например, двоичные наборы 001,100, 101 и 111 имеют десятичные номера 1,4, 5 и 7 соответственно. Тогда ФАЛ, представленная изображенной выше таблицей истинности, при числовом способе задается выражением 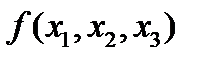 ={1,4,5,7}.
={1,4,5,7}.
4)Аналитический способ. Предполагает описание ФАЛ в виде алгебраического выражения, получаемого путем применения к аргументам операций булевой алгебры. В частности эти выражения могут быть так называемыми нормальными формами ФАЛ, о которых подробнее будет сказано ниже. Для рассмотренного выше примера ФАЛ одна из таких форм (дизъюнктивная нормальная форма) имеет следующий вид: 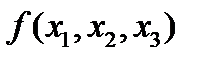 =
= 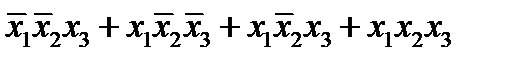 .
.
5)Графический (геометрический) способ. Булева функция задается с помощью n-мерного единичного куба. Множество наборов, на которых определена функция n переменных, представляется вершинами единичного n-мерного куба. Отметив черным цветом те вершины куба, в которых функция принимает единичное значение, получаем геометрическое представление функции. Ниже представлено задание ФАЛ, что была уже рассмотрена нами в качестве примера в описанных выше способах 2- 4.
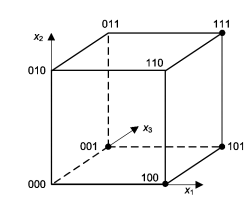
.
6)Координатный способ (карты Карно).При этом способе задания таблица истинности заменяется координатной картой состояний, известной под названием карты Карно (диаграммы Вейча). Карта Карно – это прямоугольная таблица, содержащая 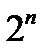 клеток по числу всех возможных наборов из n переменных. Каждой клетке сопоставляется набор аргументов ФАЛ. Этот набор по существу указывает координату этой клетки, но в явном виде эта координата в клетку карты Карно не записывается. В явном виде в клетку с этой координатой записывается значение ФАЛ, которое эта функция принимает на двоичном наборе, задаваемом координатой клетки.
клеток по числу всех возможных наборов из n переменных. Каждой клетке сопоставляется набор аргументов ФАЛ. Этот набор по существу указывает координату этой клетки, но в явном виде эта координата в клетку карты Карно не записывается. В явном виде в клетку с этой координатой записывается значение ФАЛ, которое эта функция принимает на двоичном наборе, задаваемом координатой клетки.
Все переменные ФАЛ, задаваемой картой Карно, разбиваются на две группы. При этом одна группа определяет выбор строки, вторая – выбор столбца. Разбиение на группы производится так, чтобы в соседних клетках координаты (им соответствуют входные наборы) ФАЛ различались значением только одной переменной. Две клетки считаются соседними, если они имеют общую сторону.
Карту Карно можно «свернуть» в цилиндр, соединив либо самый левый и самый правый ее столбец, либо самую верхнюю и самую нижнюю ее строки. Отсюда понятно, что соответствующие клетки карты Карно, расположенные в упомянутых крайних столбцах и крайних строках, также являются соседними (по определению соседства).
В качестве примера рассмотрим карту Карно следующего вида для функции трех переменных f(A,B,C), представленной в форме СДНФ (подробнее об этой форме будет сказано ниже):
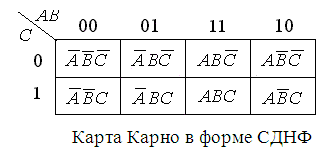
Здесь переменные разбиты на две группы - (A,B) и (С). Легко проверить, что разбиение переменных на группы и принятое в таблице соответствие между переменной (прямой или инверсной) и ее значением (0 или 1) выбрано так, что координата любой пары соседних клеток отличается только в одной позиции. Координата каждой клетки (это тройка из нулей и единиц) соответствует очевидным образом некоторому минтерму из переменных. Так, клетке с координатами (00,1) соответствует минтерм 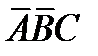 , клетке с координатами (10,0) - минтерм
, клетке с координатами (10,0) - минтерм 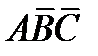 и т.д. Напомним, что в явном виде в содержимое клеток ни ее координата, ни соответствующие им минтермы не вписываются. Нами минтермы вписаны лишь с целью облегчения понимания принципа построения карты Карно. В явном виде в клетку записывается значение ФАЛ, для которой построена карта Карно. Координата клетки – это входной набор ФАЛ, само ее значение берется из последнего столбца таблицы истинности, соответствующего этому набору. Рассмотрим ФАЛ, заданную таблицей истинности в п. 2. Для нее карта Карно, построенная изложенным способом, имеет следующий вид:
и т.д. Напомним, что в явном виде в содержимое клеток ни ее координата, ни соответствующие им минтермы не вписываются. Нами минтермы вписаны лишь с целью облегчения понимания принципа построения карты Карно. В явном виде в клетку записывается значение ФАЛ, для которой построена карта Карно. Координата клетки – это входной набор ФАЛ, само ее значение берется из последнего столбца таблицы истинности, соответствующего этому набору. Рассмотрим ФАЛ, заданную таблицей истинности в п. 2. Для нее карта Карно, построенная изложенным способом, имеет следующий вид:
4.2.Таблицы истинности для элементарных ФАЛ.
В ДУ автоматики и телемеханики используются дискретные элементы, реализующие различные ФАЛ. Рассмотрим основные элементарные функции, наиболее часто используемые при синтезе упомянутых ДУ, для которых мы приведем их таблицы истинности.
1.Конъюнкция (логическое умножение, читается - И). Имеет и другие обозначения: A&B, 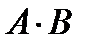 .
.

2. Дизъюнкция (логическое сложение, читается - ИЛИ). Имеет и другое обозначение: А+В. 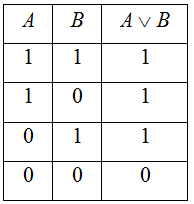
3. Импликация (логическое следствие, читается - «из А следует В»).
Дата добавления: 2018-11-25; просмотров: 1623;
