Информации в информационных системах
Восприятие информации. Восприятие информации – процесс преобразования сведений, поступающих в техническую систему или живой организм из внешнего мира, в форму, пригодную для дальнейшего использования. Благодаря восприятию информации обеспечивается связь системы с внешней средой. Современные информационные системы, создаваемые, как правило, на базе ЭВМ, в качестве своей составной части имеют более или менее развитую систему восприятия, которая может представлять собой довольно сложный комплекс программных и технических средств.
Для развитых систем восприятия можно выделить несколько этапов переработки поступающей информации: предварительная обработка для приведения входных данных к стандартному для данной системы виду, выделение в поступающей информации семантически и прагматически значимых информационных единиц, распознавание объектов и ситуаций, коррекция внутренней модели мира. В зависимости от анализаторов, входящих в комплекс технических средств системы восприятия, организуется восприятие зрительной, акустической и других видов информации.
Кроме того, различают статическое и динамическое восприятие. При динамическом восприятии особо выделяют системы, функционирующие в том же темпе, в каком происходят изменения в окружающей среде. Важнейшей проблемой восприятия информации является проблема интеграции информации, поступающей из различных источников и от анализаторов разного типа в пределах одной ситуации.
Очень кратко рассмотрим процесс восприятия наиболее важного вида информации – зрительной (напомним, что человек до 80% информацию получает именно через органы зрения). Можно выделить несколько уровней зрительного восприятия:
1. Получение изображения, поступающего от рецепторов. Как правило, к ЭВМ подключают специальные устройства цифрового ввода изображения, в которых яркость каждой точки изображения кодируется одним или несколькими двоичными числами.
2. Построение образной модели. На этом уровне с помощью специально разработанных алгоритмов происходит обнаружение объектов в описании сцены и разбиение изображений на значимые сегменты. Эффективность алгоритмов анализа сцен определяет скорость работы системы восприятия.
3. Построение образно-семантической модели. На этом уровне за счет информации, имеющейся во внутренней модели внешнего мира, и за счет знаний, хранящихся в ней, опознаются выделенные на предыдущем уровне объекты и между ними устанавливаются пространственные, временные и другие виды отношений. В технических системах на этом уровне восприятия используются методы распознавания образов. Полученные знания о текущей
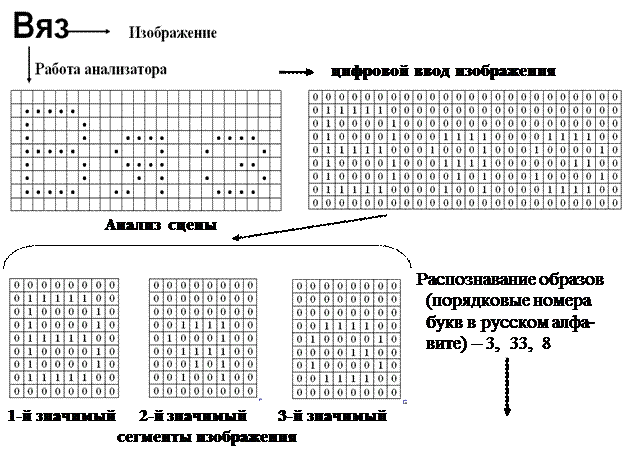
Рис. 2
ситуации могут использоваться в дальнейшей работе. Приведенный рис. 2 поясняет в общих чертах работу системы зрительного восприятия текстовой информации. (Далее возможно, например, обращение к словарю системы для обнаружения в нем считанного слова и определение его семантики).
С точки зрения информационной системы в целом, система восприятия осуществляет первичную обработку собираемой извне информации. В свою очередь, для системы восприятия первичную обработку информации производит система сбора информации. На практике часто встречаются информационные системы, не обладающие развитой системой восприятия (из-за отсутствия необходимости в таковой). В этом случае система восприятия представляет собой систему сбора информации.
Сбор информации.Система сбора информации представляет собой сложный программно-аппаратный комплекс. Как правило, современные системы сбора информации не только обеспечивают кодирование информации, ее ввод в ЭВМ, но и выполняют первичную обработку этой информации. Сбор информации – это процесс получения информации из внешнего мира и приведение ее к виду, стандартному для данной информационной системы. Обмен информацией между воспринимающей системой и окружающей средой осуществляется, как уже упоминалось, посредством сигналов.
Сигнал можно определить как средство перенесения информации в про-
| |
Совокупность технических средств ввода информации в ЭВМ, программ, управляющих всем комплексом технических средств, и программ, обеспечивающих ввод информации с отдельных устройств ввода (драйверов устройств), – вот что представляет собой современная развитая система сбора информации.
Сбор и регистрация информации происходят по-разному в различных экономических объектах. Наиболее сложна эта процедура в автоматизированных управленческих процессах промышленных предприятий, фирм и т.д., где производится сбор и регистрация первичной учетной информации, отражающей производственно-хозяйственную деятельность объекта. Особое значение при этом придается достоверности, полноте и своевременности первичной информации. На предприятии сбор и регистрация информации происходят при выполнении различных хозяйственных операций (прием готовой продукции, получение и отпуск материалов, трудозатраты на выполнение определенного производственного процесса и т.д.). сначала информацию собирают, затем ее фиксируют. Учетные данные могут возникать на рабочих местах в результате подсчета количества обработанных деталей, прошедших сборку узлов, изделий, выявление брака и т.д. Для сбора фактической информации производится измерение, подсчет, взвешивание материальных объектов, получение временных и количественных характеристик работы отдельных исполнителей. Сбор информации всегда сопровождается ее регистрацией, то есть фиксацией на материальном носителе (напомним, что информация всегда существует на каком-то материальном носителе). В системах организационно-экономического управления запись в первичные документы в основном осуществляется вручную, поэтому процедуры сбора и регистрации остаются пока наиболее трудоемкими. В технических системах автоматического управления эти операции автоматизированы за счет использования различных датчиков, измерительных и регистрирующих приборов.
Передача информации. Передача информации осуществляется различными способами: передача по телекоммуникационным каналам связи, с помощью курьера, пересылка по почте, доставка транспортными средствами и т.д. Некоторые технические средства сбора и регистрации, собирая автоматически информацию с датчиков, установленных на рабочих местах, передают ее непосредственно в ЭВМ. В современных условиях большое распространение получила распределенная обработка данных в информационно-вычислительных сетях (ИВС), которые представляют наиболее динамичную и эффективную отрасль автоматизированной технологии процессов ввода, передачи, обработки и выдачи информации. Важнейшим звеном ИВС является канал передачи данных, структурная схема которого представлена на рис. 3.
Непрерывный канал связи (НКС) совместно с функционирующими на его концах модемами образует дискретный канал связи (ДКС). В свою очередь, ДКС и устройства повышения достоверности (УПДс) образуют канал передачи данных.
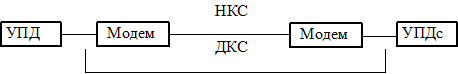
Рис. 3
УПД – устройство подготовки данных; НКС – непрерывный канал связи;
ДКС – дискретный канал связи; УПДс – устройство повышения достоверности
Модем – модулятор/демодулятор – устройство преобразования данных
В НКС элементы данных передаются в виде физических сигналов, которые описываются непрерывными функциями времени. Большинство НКС оказываются непригодными для передачи сигналов, отображающих данные. С помощью модулятора информационный сигнал воздействует на некоторый параметр сигнала – переносчика, благодаря чему спектр сигнала смещается в область частот, для которых наблюдается наименьшее затухание в выбранном НКС. Обратную операцию, переход от модулированного сигнала (сигнала – переносчика) к модулирующему (информационному сигналу), осуществляет демодулятор. Понятие ДКС позволяет, отвлекаясь от физической природы процессов, происходящих в НКС, представлять совокупность НКС и модемов на его концах как некоторый "черный ящик", на вход которого подается последовательность кодовых символов – входное сообщение. Оно может представлять собой некоторый текст на русском языке, а может быть и двоичным кодом – последовательностью нулей и единиц. Чаще всего в ИВС рассматриваются ДКС с двоичным алфавитом, когда входное и выходное сообщения представляют собой двоичные кодовые последовательности.
Завершая общее описание канала связи, рассмотрим УПДс. УПДс может представлять собой специальную аппаратуру, предназначенную для повышения достоверности передачи данных, а может, особенно в современных ИВС, представлять собой специальную программу и ЭВМ, на которой она выполняется, может являться как элементом канала связи, так и элементом системы обработки информации. Повышение помехоустойчивости и защищенности передаваемой информации в каналах связи подробнее рассмотрено в лекции 7.
Лекция 6
Системы счисления
Рассмотрим некоторый класс знаковых систем – системы счисления. Система счисления – это совокупность приемов и способов обозначения(записи) чисел. Системы счисления бывают двух типов: позиционные и непозиционные. Позиционной называется система счисления, в которой значение (величина) цифры зависит от позиции (места) ее в числе. Если такой зависимости нет, то система счисления называется непозиционной.
Системы счисления – результат длительного исторического развития записи чисел, начавшегося, видимо, с возникновения так называемой единичной системы счисления, в которой для записи чисел применялся только один вид знаков – “палочка”. Каждое число в такой системе счисления обозначалось с помощью “строки”, составленной из “палочек”, количество которых равнялось обозначаемому числу. Если считать “палочку” за цифру 1, то можно единичную систему счисления отнести к позиционной с основанием 1.
Одна из немногих непозиционных систем счисления, которая сохранила свое значение в настоящее время, – это римская система счисления. Алфавитом ее являются несколько заглавных латинских букв: I, V, X, L, C, D и М, с помощью которых записываются соответственно числа: I=1, V=5, X=10, L=50, C=100, D=500, М=1000. Конструкциями этого алфавита являются различные натуральные числа, причем одна и та же цифра, стоящая в разных местах (позициях) числа, не меняет своего значения, например, XII=12, МСМХСIX=1999, XLVIII=48 и т.д. Здесь цифры М, С, Х, I, независимо от их расположения в числе, сохраняют свое номинальное значение.
Синтаксис, или правила записи чисел в римской системе счисления:
· если более значимая цифра стоит перед меньшей цифрой или если подряд стоящие цифры одинаковы, то они арифметически складываются, например, XXXVI=36;
· если меньшая цифра стоит перед бóльшей, то она вычитается из бóльшей, причем меньшая цифра в этом случае повторяться подряд не может, например, XL=40, CDIV=404 (но нельзя IIV=3);
· цифры M, C, X, I могут повторяться в записи числа не более трех раз подряд, а цифры D, L, V– по одному разу.
Самое большое число в этой системе, очевидно, MMMCMXCIX=3999. Для записи еще больших чисел надо расширять алфавит языка, то есть вводить новые цифры (буквы). По этой причине, а также из-за отсутствия цифры 0 римская система счисления не годится для записи действительных чисел. Теперь попробуйте перемножить два числа CLVI и LXXIV, не прибегая к переводу их в привычную для нас систему счисления. Думаю, что это вам не удастся. Сейчас римская система счисления используется в основном для обозначения веков, томов книг, на циферблатах часов и т.д. Из рассмотренного вытекают следующие недостатки непозиционных систем счисления:
· в них нельзя записать любое число;
· запись чисел громоздка и неудобна;
· арифметические операции над числами крайне затруднены.
По этим причинам используются позиционные системы счисления, в которых каждая цифра, содержащаяся в записи числа, занимает определенное место, называемое разрядом. Отсчет разрядов производится справа налево. Единица каждого следующего разряда всегда больше единицы предыдущего разряда в определенное число раз, равное количеству цифр, принятому для записи чисел. Это определенное число носит название основания системы счисления. Классический пример позиционной системы счисления – десятичная, к которой мы привыкли с детства, и которая получила в мире самое широкое распространение.
Каждая цифра позиционной системы счисления несет в себе двойную нагрузку: собственное значение и значение, принимаемое ею в зависимости от позиции в числе. Например, в числе 3983763 одна и та же цифра 3 принимает значение три, три тысячи и три миллиона в зависимости от ее позиции (разряда) в числе.
Десятичная система счисления возникла приблизительно в V веке новой эры в Индии. Первыми о ней узнали арабы, которые в VII-VIII веках завоевали обширные районы Азии и Средиземноморья. Поскольку Европа узнала о ней от арабов, то алфавит десятичной системы счисления стали называть арабскими цифрами. Правила выполнения основных арифметических операций в ней впервые были разработаны выдающимся восточным математиком и астрономом Мухаммедом аль-Хорезми и описаны им в труде, который назывался “Книга о сложении и вычитании по исчислению индийцев”.
Если обозначить в позиционной системе счисления разряд числа буквой R, то любое действительное число и его значение можно представить в виде полинома:
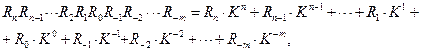где n – количество цифр в целой части; m – количество цифр в дробной части числа (после запятой), К – основание системы счисления, а R – любые цифры, принятые в данной системе счисления (разряды). Задавая различные значения К, можно получить множество различных позиционных систем счисления. Откуда вытекают их общие свойства:
· благодаря поразрядной организации записи чисел в позиционной системе счисления с ними легко проводить арифметические операции;
· при переходе в числе на один разряд влево (вправо) значение цифры увеличивается (уменьшается) во столько раз, чему равно основание системы;
· в позиционных системах счисления запись чисел удобна и компактна: в них можно записать любое число – сколь угодно большое или сколь угодно малое, чего нельзя сделать в непозиционных.
С развитием вычислительной техники большое значение приобрели позиционные системы счисления с основанием, отличным от десяти.
Несмотря на то, что исторически человек привык работать с числами в десятичной системе счисления, для хранения, обработки и передачи информации в технических устройствах она крайне неудобна.
Во-первых, числа в электронные схемы устройств не запишешь так, как ручкой или карандашом на бумаге. Это можно сделать, если каждой цифре ставить в соответствие какое-то фиксированное состояние технического элемента, причем таких состояний должно быть десять, и они друг от друга должны резко отличаться, иначе устройство не определит, с какой цифрой имеет дело. Но, практически какой бы элемент технической базы устройств мы ни взяли, обнаруживается только два резко отличных друг от друга состояния. Примеры: магнитный элемент – намагничен/размагничен; электрический конденсатор – заряжен/разряжен; контакт реле – замкнут/разомкнут; полупроводниковый прибор – проводит/не проводит ток и т.д. Отсюда вывод: с помощью имеющихся в настоящее время технических элементов электронных устройств можно отражать только две цифры – 0 и 1. При этом информация хранится до тех пор, пока хранится состояние элемента, соответствующее ей.
Во-вторых, информацию между устройствами нужно передавать какими-то сигналами, причем устройство должно четко и однозначно определять, что один сигнал – это цифра 2, а другой сигнал – цифра 7. При использовании десятичной системы счисления таких сигналов должно быть десять, и они должны так же четко отличаться друг от друга, как и состояния элементов. Учитывая, что устройства информационной техники – это в основном электрические устройства (электронные), то из резко отличных друг от друга дискретных сигналов можно выбрать опять только два – есть импульс тока/нет импульса тока. С помощью этих сигналов можно передавать только две цифры – 1 и 0.
В-третьих, чем меньше различных сигналов в цепях устройств, тем проще схемы, тем менее они затратны и тем надежнее работают.
Именно поэтому в устройствах информационной техники применяется двоичная система счисления, использующая две цифры (0 и 1) для представления любых чисел. Числа в двоичной системе счисления записываются так же, как в десятичной системе счисления, один разряд за другим. Число и его значение по-прежнему представляются в виде полинома:
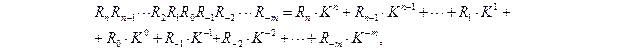
Здесь отличие только в том, что разряд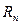 
может принимать значения 0 или 1. Например:
100111,101=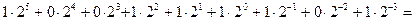 
39,62510.
Все арифметические операции над числами в двоичной системе счисления выполняются точно так же, как и в десятичной (поразрядно, по тем же правилам), только нужно помнить, что 1 при переходе из соседнего разряда изменяет свое значение в два раза, а не в десять. Примеры:
1001011101 (605) 1001011101 (605) 1101 (13) 1011011 (91)│1101 (13)
+ 10111011 (187) - 10111011 (187) х 111 (7) - 1101 111 (7)
1100011000 (792) 110100010 (418) 1101 10011
+ 1101 - 1101
1101 1101
1011011 (91) - 1101
0000
Очевидно, что сдвиг двоичного числа вправо или влево на n разрядов уменьшает или увеличивает его в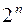 
раз. Это широко применяется в информационных устройствах путем использования специальных схем – сдвиговых регистров, особенно в операциях умножения и деления, которые заменяются многократными операциями сложения и вычитания, где сдвиги чисел необходимы. Основанием системы является число 2 (записывается как 10, то есть одна двойка и ноль единиц).
Перекодировка в двоичную систему счисления производится автоматически программным путем при вводе информации в компьютер, а из двоичной системы – при выводе на экран или печать.
Простота действий над двоичными числами определяет простоту построения электронных схем для их выполнения. Кроме того, как мы увидим дальше, в двоичной системе счисления, то есть с помощью цифр 0 и 1 можно записать в память компьютера любую информацию (числовые данные, текст, графику, музыку, видеоизображения, кинокадры или сигналы от устройств управления объектами и др.) и обработать ее.
Сравнивая записи чисел в десятичной и двоичной системах счисления, нетрудно заметить, что в двоичной системе счисления для записи чисел требуется значительно больше разрядов. Таким образом, выигрывая в простоте, мы проигрываем в компактности записи чисел и ее наглядности. Поэтому в вычислительной технике нашли широкое применение системы счисления, основания которых кратны двум, –восьмеричная и шестнадцатеричная.По существу, это разновидности записи двоичных чисел выполненные более компактно другими символами.
В восьмеричной системе счисления используются первые восемь арабских цифр, и основание ее – 8=23 – записывается в виде 10, то есть одна восьмерка и ноль единиц.
В шестнадцатеричной системе счисления используется 16 символов для записи чисел – это десять арабских цифр и шесть начальных букв латинского алфавита: 0,1,2,...,9,A,B,C,D,E,F. Основание ее – 16=24 – записывается также в виде 10, то есть одна шестнадцатеричка и ноль единиц. Для обозначения шестнадцатеричных чисел обычно за числом записывают латинскую букву H или h, например, 6АВ72EDC98h.
Каждая цифра в восьмеричной системе счисления записывается тремя двоичными цифрами (2 в степени 3), а каждая цифра шестнадцатеричной системы счисления – четырьмя двоичными цифрами (2 в степени 4). Разбиение двоичного числа на триады или тетрады производится справа. Недостающие цифры слева в самой левой триаде или тетраде дополняются нулями, например: 25510=111111112=011 111 111=3778=1111 1111=FF16.
Следует подчеркнуть, что эти системы счисления используются только для удобства отображения пользователю на устройствах вывода находящейся в памяти информации. Внутри же компьютера информация не может быть записана иначе как в двоичной системе счисления.
Для перевода целых чисел из одной системы счисления в другую нужно исходное число и получающиеся частные от деления делить последовательно на основание системы счисления, в которую оно переводится, записанное в исходной системе счисления. Получающиеся остатки от деления и последнее частное, меньшее делителя, и есть цифры числа новой системы счисления, записанные в исходной. Последнее частное от деления будет старшим разрядом числа. Поэтому записывать число в новой системе счисления нужно, начиная с него. Получаем число в новой системе счисления.
Для перевода дробей нужно дробную часть числа и дробные части получающихся промежуточных произведений умножать на основание новой системы счисления, записанное в исходной, до тех пор, пока в дробной части промежуточного произведения не получатся все нули или пока не будет достигнута требуемая точность (количество цифр в новой системе счисления). Цифры в целой части промежуточных произведений и есть цифры новой системы счисления, записанные в исходной системе счисления. Записывая их последовательно от начала к концу, получим число в новой системе счисления.
Перевод чисел из любой системы счисления в десятичную систему на практике проще и удобнее выполнять путем суммирования всех разрядов числа, записанного в виде полинома, как было показано ранее.
Лекция 7
Дата добавления: 2018-11-25; просмотров: 566;