Определение оптимального режима тренировок элементов КСНО

Надежность КСНО характеризуется вероятностью безотказной работы, которая, в свою очередь, складывается из вероятностей безотказной работы составляющих элементов КСНО Очевидно, выбор оптимальных характеристик этих элементов обеспечивает оптимальность всего комплекса в целом.

Одним из путей повышения надежности элемента является его испытания в течение определенного времени с последующей постановкой на агрегат КСНО тех элементов, которые не отказали за время этих испытаний.

Оптимальный режим тренировки элемента КСНО определяется временем испытания этого элемента 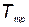, после которого вероятность безотказной работы элемента 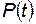в течение заданного времени t максимальна.

Если обозначить через 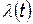интенсивность отказов элемента после тренировки, то средняя интенсивность отказов в течение времени t будет

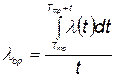. (5.75)

Для определения минимальной 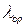приравняем производную 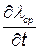нулю:

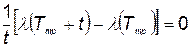. (5.76)

Это уравнение позволяет определить 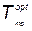, если известен вид функции .

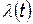При определении 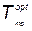мы воспользовались тем обстоятельством, что при минимальной средней интенсивности отказов вероятность безотказной работы максимальна. Если необходимо найти оптимальное время тренировки, минимизирующее суммарные затраты, то поступают следующим образом.

Пусть стоимость одного элемента КСНО равна 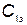, стоимость единицы времени тренировки 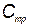и ущерб от отказа элемента 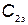. Всего в КСНО используется N элементов.

Количество не отказавших за время тренировок элементов должно быть равно N элементам, используемым в КСНО:

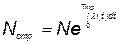, (5.77)

где 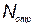— количество элементов, поставленных на тренировку.

После тренировки не откажет 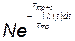элементов, а откажет соответственно

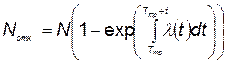. (5.78)

Определим суммарные затраты, которые включают в себя:

а) стоимость элементов, поставленных на тренировку:

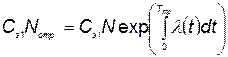; (5.79)

б) стоимость тренировки

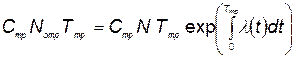; (5.80)

(здесь предполагается, что отказавшие элементы с испытаний не снимаются до конца тренировки);

в) ущерб от отказа элементов:

, (5.81)

т. е.

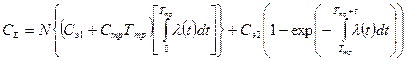. (5.82)

Для определения оптимального времени тренировки 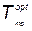необходимо от 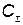взять производную по 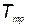и приравнять нулю:

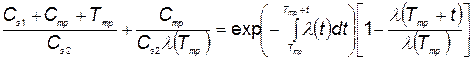. (5.83)

Решение этого уравнения удобно проводить графически, для чего строятся графики правой и левой частей уравнения как функции от 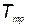и находится точка пересечения.