Сложение двух моментов количества движения

Пусть имеется система, состоящая из двух подсистем 1 и 2. Состояние этих подсистем определяется соответственно векторами моментов количества движения .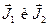

Допустим далее, что операторы проекций этих моментов коммутируют, то есть

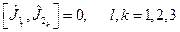или x,y,z (2.2.1)

Тогда полная система может находиться в состояниях, в которых одновременно определенное значение имеют операторы квадратов моментов подсистем:

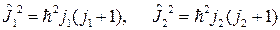(2.2.2),

и их проекции на одну из осей координат, которую мы примем за ось :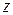

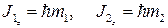(2.2.3).

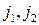- квантовые числа, определяющие собственные значения операторов моментов 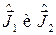соответственно. 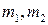- квантовые числа, определяющие собственные значения операторов проекции моментов 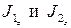соответственно.

Если подсистемы не взаимодействуют друг с другом, то состояние системы описывается ВФ, являющейся произведением волновых функций двух подсистем:

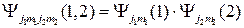(2.2.4),

где

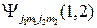- ВФ полной системы, 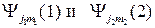- волновые функции подсистем 1 и 2 соответственно или в дираковском обозначении:

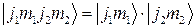(2.2.5).

При фиксированных 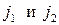имеется 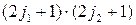различных функций (2.2.4) или (2.2.5), отличающихся значениями пары чисел .

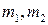Если между подсистемами имеется взаимодействие, то моменты отдельных подсистем не сохраняются, и хорошими квантовыми числами будут лишь полный момент количества движения системы 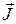и его проекция .

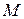Однако, если взаимодействие не слишком сильно, то в нулевом приближении можно считать, что не сохраняются только проекции моментов подсистем 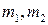, а моменты 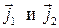сохраняют свои значения. В этом случае состояние системы характеризуется четырьмя квантовыми числами 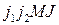и описываются ВФ 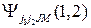, представляющей собой линейную комбинацию волновых функций подсистем:

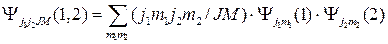(2.2.6)

или в дираковском обозначении:

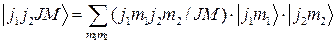(2.2.7).

Коэффициенты этой линейной комбинации 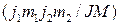называются коэффициентами векторного сложения или коэффициентами Клебша – Гордана, а сама процедура перехода от моментов 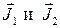и их проекций 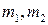для отдельных подсистем к суммарному моменту количества движения 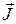называется векторным сложением угловых моментов. Оператор полного момента системы 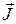равен векторной сумме операторов моментов подсистем 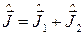. Коэффициенты 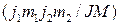определяют вклад различных функций (2.2.5)

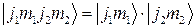в (2.2.7)

.

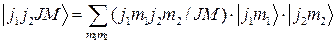При рассмотрении векторного сложения моментов возникают два основных вопроса:

1) Какие значения может принимать полный момент системы 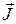при заданных моментах подсистем .

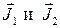2) Как вычисляются коэффициенты векторного сложения, необходимые для построения волновых функций (2.2.6) или (2.2.7), которые будут описывать состояние системы.

Ответ на первый вопрос дает известное из квантовой механики правило векторного сложения моментов количества движения, которое гласит, что при сложении двух моментов 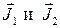суммарный момент 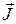может принимать значения:

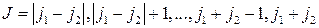(2.2.8).

На основе принципа суперпозиции можно выяснить физический смысл коэффициентов векторного сложения.