Оператор момента количества движения

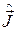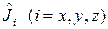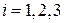В общем случае оператором момента количества движения, или, кратко, оператором момента называется вектор , декартовы координаты которого (или ) являются эрмитовыми операторами, удовлетворяющими перестановочным соотношениям (2.1.1):

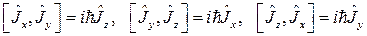
(2.1.1).

Перестановочные соотношения (2.1.1) можно записать также в форме:

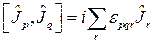(2.1.2),

где 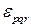- антисимметричный единичный тензор третьего ранга с компонентой .

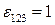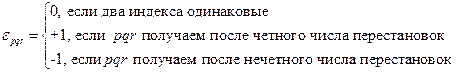
Здесь под 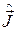подразумевается орбитальный 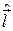, спиновый 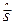, либо полный момент количества движения 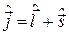одной частицы и то же самое для системы частиц:

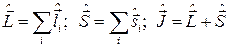. (2.1.3).

Введем оператор квадрата момента

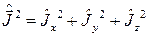(2.1.4).

Оператор квадрата момента 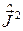и любая из проекций момента 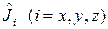(или 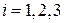) коммутируют, то есть

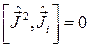. (2.1.5).

Из перестановочных соотношений (2.1.1) и (2.1.5) следует, что одновременно определенные значения могут иметь квадрат момента и одна из его проекций. Примем в качестве этой проекции .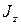

Оператор квадрата момента 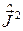и оператор проекции момента 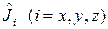(или 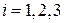) коммутируют, следовательно, эти операторы имеют общую систему собственных функций. Обозначим эти функции через:

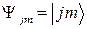- дираковское обозначение (2.1.6),

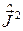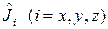(2.1.6) – собственные функции операторов и (или ).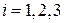

Следовательно, выполняются операторные равенства (2.1.7) и (2.1.8):

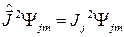(2.1.7)

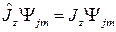(2.1.8)

или в дираковском обозначении:

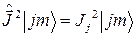, (2.1.7’)

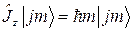(2.1.8’)

где 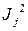и 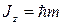- собственные значения операторов 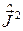и 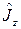соответственно.

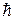- приведенная постоянная Планка.

Квантовые числа 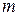, определяющие собственные значения оператора проекции 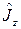в уравнениях (2.1.8) и (2.1.8´), пробегают отличающиеся на единицу значения, лежащие в интервале

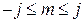(2.1.9),

где 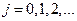- либо 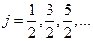(2.1.10).

Собственные значения оператора квадрата момента 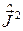определяются квантовыми числами 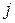с помощью формулы:

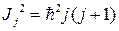(2.1.11).

То есть, с учетом (2.1.9), (2.1.10),и (2.1.11) выражения (2.1.7) и (2.1.8) мы можем переписать в виде:

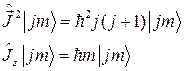
где 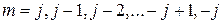, то есть, всего 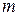принимает ( 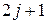) различных значений.

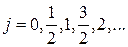
Введем вспомогательные неэрмитовые операторы

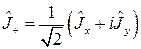(2.1.12),

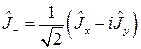(2.1.13).

Назовем эти операторы операторами рождения (2.1.12) и уничтожения (2.1.13) соответственно.

Из выражений (2.1.12) и (2.1.13) видно, что операторы 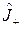и 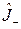переходят друг в друга при эрмитовом сопряжении:

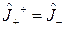(2.1.14),

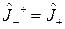(2.1.15).

Для этих операторов можем написать следующие перестановочные соотношения:

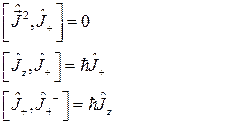(2.1.16).

Операторы 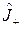и 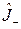имеют диагональные матричные элементы по квантовому числу 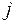. Оператор 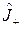увеличивает, а оператор 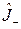уменьшает квантовое число 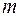на единицу.

Отличными от нуля матричными элементами операторов 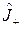и 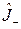являются

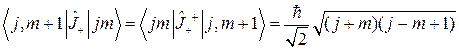(2.1.17).

Зная отличные от нуля матричные элементы (2.1.17), можно вычислить и матричные элементы операторов 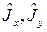. Используя равенства

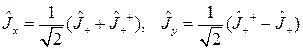(2.1.18),

находим

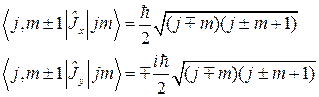(2.1.19).

Согласно (2.1.4) и (2.1.12), (2.1.13) имеем

.

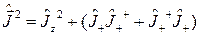Поэтому, учитывая (2.1.8´) и (2.1.17), находим

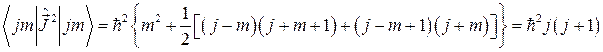
(2.1.20)

Соотношения (2.1.1) – (2.1.20) справедливы не только для любых угловых моментов, но также для произвольных эрмитовых операторов, подчиняющихся соотношениям (2.1.1) и (2.2.2), например, для операторов изотопического спина 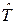, различных видов квазиспинов, псевдоспинов, операторов 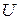- спина, 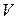- спина и т.п., используемых в теории элементарных частиц и в теории ядра.