Задачи, связанные с взаимным расположением прямых
Рассмотрим некоторые задачи аналитической геометрии, которые связаны с взаимным расположением прямых в пространстве.
ЗАДАЧА 2. Найти угол между пересекающимися (скрещивающимися) прямыми в пространстве.
ОПРЕДЕЛЕНИЕ. Углом между двумя скрещивающимися прямыми 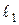 и
и 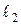 называется угол между прямой
называется угол между прямой 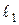 и проекцией прямой
и проекцией прямой 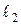 на любую плоскость, проходящую через прямую
на любую плоскость, проходящую через прямую 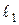 .
.
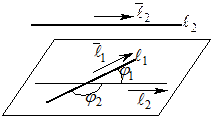 Иначе говоря, угол между скрещивающимися прямыми – это угол между двумя пересекающимися прямыми, параллельными данным.
Иначе говоря, угол между скрещивающимися прямыми – это угол между двумя пересекающимися прямыми, параллельными данным.
Пусть даны две пересекающиеся или скрещивающиеся прямые:
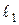 :
: 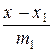
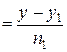
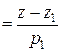 и
и 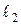 :
: 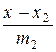
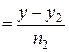
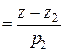 .
.
Обозначим 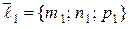 ,
, 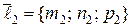 – направляющие векторы первой и второй прямой соответственно.
– направляющие векторы первой и второй прямой соответственно.
Так как один из углов 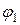 между прямыми равен углу между их направляющими векторами, а второй угол
между прямыми равен углу между их направляющими векторами, а второй угол 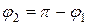 , то углы
, то углы 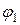 и
и 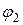 могут быть найдены по формуле
могут быть найдены по формуле
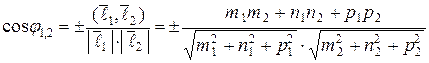 ,
,
или 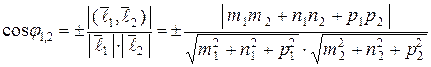 ,
,
где знак плюс берется в том случае, когда надо найти величину острого угла, а знак минус – когда надо найти величину тупого угла.
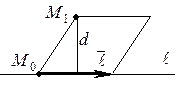 ЗАДАЧА 3. Найти расстояние от точки до прямой в пространстве.
ЗАДАЧА 3. Найти расстояние от точки до прямой в пространстве.
Пусть дана прямая
 :
: 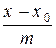
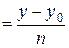
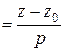
и 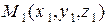 – точка, не принадлежащая этой прямой. Обозначим
– точка, не принадлежащая этой прямой. Обозначим 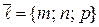 – направляющий вектор прямой
– направляющий вектор прямой 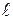 ,
, 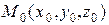 – точка на прямой
– точка на прямой 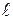 ,
, 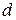 – расстояние от точки
– расстояние от точки 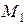 до
до 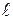 .
.
Рассмотрим параллелограмм, построенный на векторах 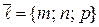 и
и 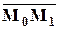 . Тогда
. Тогда 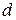 – высота этого параллелограмма, опущенная из вершины
– высота этого параллелограмма, опущенная из вершины 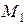 . Следовательно,
. Следовательно,
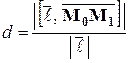 .
.
ПРИМЕР. Найти расстояние 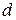 от точки
от точки 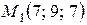 до прямой
до прямой 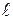 :
: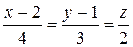 .
.
Из условия задачи имеем: 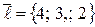 ,
, 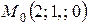 . Тогда
. Тогда
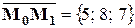 ,
,
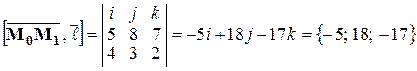 ,
,
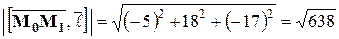 ,
, 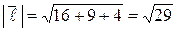 ,
,
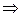
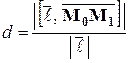
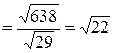 – искомое расстояние.
– искомое расстояние.
ЗАДАЧА 4. Найти расстояние между скрещивающимися прямыми.
ОПРЕДЕЛЕНИЕ. Расстоянием между двумя скрещивающимися прямыми называется длина их общего перпендикуляра.
Пусть даны две скрещивающиеся прямые
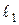 :
: 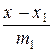
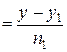
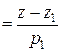 и
и 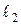 :
: 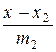
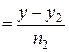
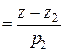 ,
,
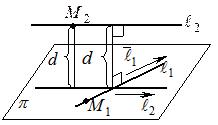 и
и 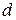 – расстояние между
– расстояние между 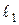 и
и 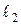 .
.
Построим плоскость 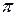 , проходящую через прямую
, проходящую через прямую 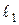 параллельно
параллельно 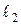 . Тогда
. Тогда 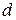 – расстояние от прямой
– расстояние от прямой 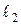 до плоскости
до плоскости 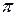 . Найти это расстояние можно по формуле:
. Найти это расстояние можно по формуле:
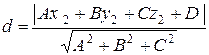 ,
,
где 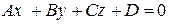 – общее уравнение плоскости
– общее уравнение плоскости 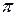 ,
,
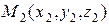 – любая точка на прямой
– любая точка на прямой 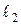 .
.
ПРИМЕР. Найти расстояние 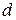 между двумя прямыми
между двумя прямыми
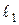 :
: 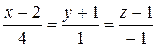 и
и 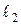 :
: 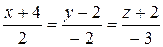 .
.
1) Прежде всего, установим взаимное расположение данных прямых. По условию задачи: 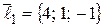 и
и 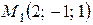 – направляющий вектор и фиксированная точка первой прямой,
– направляющий вектор и фиксированная точка первой прямой, 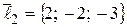 и
и 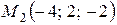 – направляющий вектор и фиксированная точка второй прямой;
– направляющий вектор и фиксированная точка второй прямой; 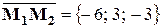 . Имеем:
. Имеем:
1) 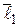 ∦
∦ 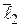 – прямые не параллельны;
– прямые не параллельны;
2) вычислим 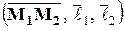 :
:
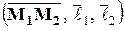
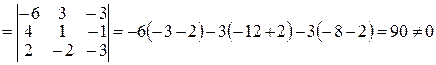 .
.
Следовательно, данные прямые являются скрещивающимися.
2) Запишем уравнение плоскости  , проходящей через прямую
, проходящей через прямую 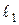 параллельно
параллельно 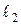 :
:
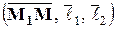
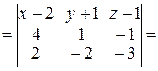
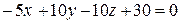
 :
: 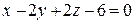 .
.
Тогда 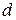 – расстояние от точки
– расстояние от точки 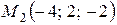 до плоскости
до плоскости  :
:
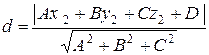
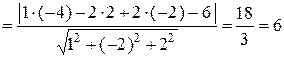 .
.
Замечание. Предложенный способ нахождения расстояния между скрещивающимися прямыми – не единственный. Можно найти это расстояние, используя векторную алгебру.
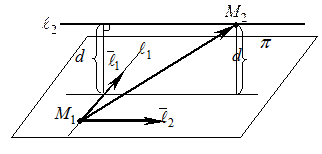 |
Действительно, построим на векторах
 ,
,  и
и 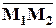 пирамиду.
пирамиду.
Тогда 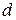 – высота пирамиды, опущенная из точки
– высота пирамиды, опущенная из точки 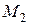 и, следовательно,
и, следовательно,
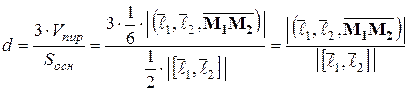
ЗАДАЧА 5. Найти точку пересечения прямых.
Пусть даны две пересекающиеся прямые
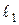 :
: 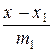
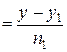
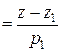 и
и 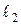 :
: 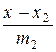
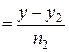
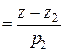 ,
,
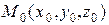 – точка пересечения прямых. Тогда
– точка пересечения прямых. Тогда 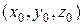 – решение системы уравнений
– решение системы уравнений
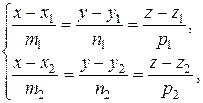
или, переходя к параметрическим уравнениям прямой,
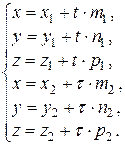
ПРИМЕР. Найти точку пересечения прямых
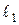 :
: 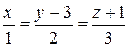 и
и 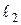 :
: 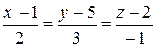 .
.
1) Прямые 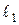 и
и 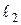 не являются параллельными (их направляющие векторы не коллинеарны) и для них выполняется условие (9):
не являются параллельными (их направляющие векторы не коллинеарны) и для них выполняется условие (9):
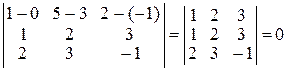 .
.
Следовательно, прямые 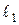 и
и 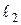 – пересекаются.
– пересекаются.
2) Найдем точку пересечения прямых. Для этого перейдем к их параметрическим уравнениям:
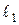 :
: 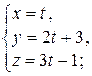 и
и 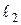 :
: 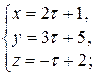
и решим систему
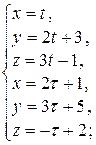
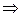
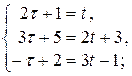
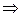
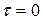 ,
, 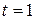 ;
;
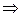
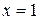 ,
, 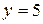 ,
, 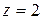 .
.
Таким образом, точкой пересечения прямых является точка 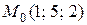
Дата добавления: 2018-11-25; просмотров: 351;
