Простая индуктивная высокочастотная коррекция
Рассмотрим принципиальную схему усилителя с индуктивной высокочастотной коррекцией, приведенную на рис.8.1.

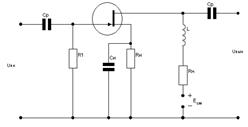
Рис.8.1.Схема индуктивной высокочастотной коррекции
Корректирующим элементом является индуктивность L, включенная последовательно с сопротивлением нагрузки 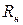 . Индуктивность L выбирается настолько малой, что ее влиянием в области низких и средних частот можно пренебречь. На высоких частотах индуктивное сопротивление XL=jωL возрастает, вследствие чего увеличивается выходное напряжение и коэффициент усиления. Построим эквивалентную схему усилителя с индуктивной коррекцией в области высоких частот, рис.8.2.
. Индуктивность L выбирается настолько малой, что ее влиянием в области низких и средних частот можно пренебречь. На высоких частотах индуктивное сопротивление XL=jωL возрастает, вследствие чего увеличивается выходное напряжение и коэффициент усиления. Построим эквивалентную схему усилителя с индуктивной коррекцией в области высоких частот, рис.8.2.
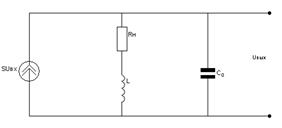
Рис.8.2. Эквивалентная схема с ВЧ коррекцией.
При построении эквивалентной схемы влиянием 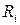 и R1 можно пренебречь, поскольку в импульсных усилителях выполняются условия:
и R1 можно пренебречь, поскольку в импульсных усилителях выполняются условия: 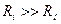 и
и 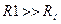 . Индуктивность L входит в выходную цепь параллельно емкости С0, в результате чего проводимость jωC0 частично компенсируется проводимостью этой индуктивной ветви. Принцип коррекции амплитудно-частотной характеристики при индуктивной высокочастотной коррекции можно объяснить следующим образом. Корректирующая индуктивность L, вводимая последовательно с резистором
. Индуктивность L входит в выходную цепь параллельно емкости С0, в результате чего проводимость jωC0 частично компенсируется проводимостью этой индуктивной ветви. Принцип коррекции амплитудно-частотной характеристики при индуктивной высокочастотной коррекции можно объяснить следующим образом. Корректирующая индуктивность L, вводимая последовательно с резистором 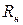 , образует в эквивалентной схеме каскада для верхних частот параллельный резонансный контур с емкостью C0. На резонансной частоте
, образует в эквивалентной схеме каскада для верхних частот параллельный резонансный контур с емкостью C0. На резонансной частоте 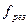 сопротивление контура увеличивается, за счет чего происходит подъем частотной характеристики в области верхних частот, рис.8.3,а.
сопротивление контура увеличивается, за счет чего происходит подъем частотной характеристики в области верхних частот, рис.8.3,а.
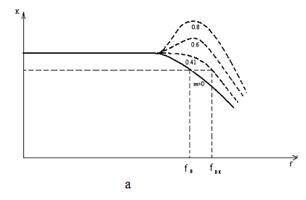
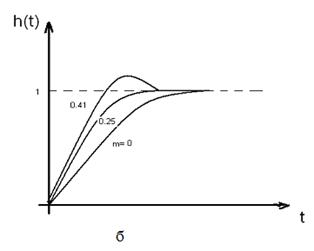
Рис.8.3. Характеристики при индуктивной коррекции:
а-частотная, б-переходная.
Причем подъем частотной характеристики зависит от добротности контура, при большой добротности на АЧХ появляется резонансный выброс, что является нежелательным явлением. Нас интересует оптимальная, равномерная частотная характеристика.
Улучшение переходной характеристики при индуктивной коррекции в импульсных усилителях объясняется следующим образом (рис. 8.3,б): в момент подачи скачка напряжения индуктивность имеет бесконечно большое сопротивление, в связи с этим весь ток SUвх протекает по цепи Cо, и в результате этогоускоряется заряд этой емкости Cо.
Рассмотрим количественный анализ индуктивной высокочастотной коррекции:
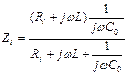
Знаменатель последнего выражения приводим к общему знаменателю 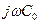 . Вторые члены числителя и знаменателя умножаем и делим соответсвенно на
. Вторые члены числителя и знаменателя умножаем и делим соответсвенно на 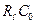 и
и 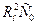 .
.
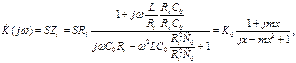 (8.1)
(8.1)
где 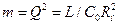 - коэффициент коррекции, равный квадрату добротности контура,
- коэффициент коррекции, равный квадрату добротности контура, 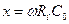 - нормированная частота. Из выражения (8.1) модуль частотной характеристики запишется в виде:
- нормированная частота. Из выражения (8.1) модуль частотной характеристики запишется в виде:
 (8.2)
(8.2)
Г.В. Брауде показал, что оптимальная частотная характеристика соответствует когда коэффициент при х2 числителя и знаменателя равны: m2=1+2m. Решив это квадратное уравнение получем оптимальный коэффициент коррекции 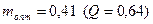 . Верхнюю граничную частоту и площадь усиления с простой высокочастотной коррекцией можно выразить:
. Верхнюю граничную частоту и площадь усиления с простой высокочастотной коррекцией можно выразить:
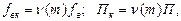 (8.3)
(8.3)
где 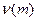 - коэффициент, определяющий выигрыш за счет коррекции. Например, при m=0,41 этот выигрыш равен 1,72. Высокочастотная коррекция увеличивает площадь усиления каскада, и, соответственно, повышает его коэффициент усиления при заданной полосе усиливаемых частот, что позволяет уменьшить количество каскадов в усилителе.
- коэффициент, определяющий выигрыш за счет коррекции. Например, при m=0,41 этот выигрыш равен 1,72. Высокочастотная коррекция увеличивает площадь усиления каскада, и, соответственно, повышает его коэффициент усиления при заданной полосе усиливаемых частот, что позволяет уменьшить количество каскадов в усилителе.
Оптимальная (без выбросов) переходная характеристика усилителя получается при m=0,25. При дальнейшем увеличении m в переходной характеристике появляются выбросы переднего фронта. В частности, при значении коэффициента коррекции m=0,41, которому соответствует оптимальная амплитудно-частотная характеристика, выброс имеет высоту около 2,5%.
Дата добавления: 2018-09-24; просмотров: 537;
