Анализ импульсного усилителя в области больших времен

Область больших времен - эта область низких частот. Низкими частотами формируется плоская вершина импульса. В области больших времен влиянием C_о можно пренебречь, так как C_о зарядится мгновенно (за время ) и за время длительности импульса τ_и не будет оказывать своего влияния. Поэтому эквивалентная схема импульсного усилителя в области больших времен имеет вид, рис.7.5.

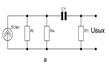
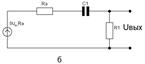
Рис.7.5. Эквивалентная схема ИУ в области больших времен.

Емкость С1 имеет большой номинал, поэтому заряжается медленно. По мере заряда С1 напряжение U_С1 возрастает, вследствие чего уменьшается 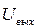. Таким образом, за счет процесса заряда емкости С1 происходит спад плоской вершины импульса на выходе усилителя.

Рассмотрим количественный анализ переходной характеристики в области больших времен. Считаем, что на вход усилителя поступает единичный импульс (7.1). В момент времени:

1.t=0; X_С1=0; U_С1=0 выходное напряжение определяется:

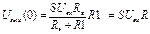, где R=R_эR1/ (R_э+ R1)

2. t > 0; 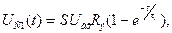где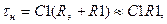

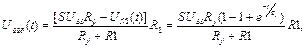
По условию анализа U_вх=1, следовательно, переходная характеристика в облости больших времен определяется выражением:

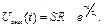(7. 8)

Нормированная переходная характеристика в области больших времен при подаче на вход единичного импульса U_вх =1;

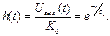(7.9)

Согласно выражению (7.9) можно построить график переходной характеристики в области больших времен, рис.7.6

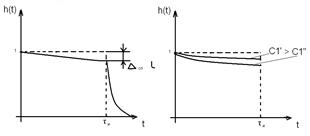
Рис.7.6. График переходной характеристики ИУ в области больших времен

За счет влияния 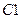переходная характеристика имеет спад плоской вершины: абсолютный спад Δ_сп =h(0)-h(t_и), относительный спад:

(7.10)

Применив разложение в ряд Маклорена (так как ) и ограничиваясь первыми двумя членами ряда, получим:

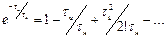
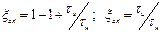(7.11)

Из выражения (7.11) видно, что для улучшения переходной характеристики в области больших времен 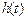, т.е. для уменьшения 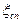, необходимо увеличитьt_н, т.е. увиличить номинал С1.

В многокаскадных усилителях общий спад равен

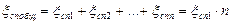
Следовательно, спад плоской вершины одного каскада можно определить выражением ₁= _общ/n, где n-количество каскадов.

Лекция №8