КОНИЧЕСКИЕ ПОВЕРХНОСТИ

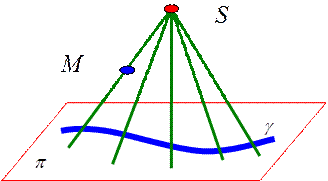Определение 1. Конической поверхностью или конусом с вершиной в точке S называется поверхность, которая обладает тем свойством, что вместе с каждой своей точкой М, отличной от точки S, эта поверхность содержит прямую SМ, пересекающую данную в плоскости π линию γ.

Эта линия γ называется направляющей поверхности, а прямые SМ - образующими.

Теорема: Коническая поверхность, направляющая которой в некоторой декартовой системе координат задана уравнением

γ: ,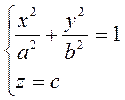

а вершина совпадает с началом координат, определяется уравнением: 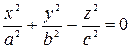(*), где 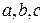- действительные числа.

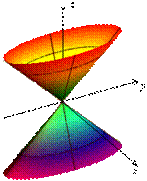
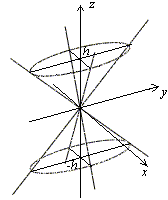
Конус

Примечание: Аналогично, если

1) γ: 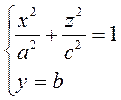, а вершина совпадает с началом координат, то уравнение конической поверхности: .

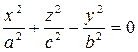2) γ: 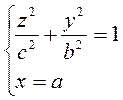, а вершина совпадает с началом координат, то уравнение конической поверхности: .

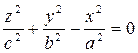Если в уравнении (*) а = в,т.е. γ – окружность, то такая коническая поверхность называется круговым конусом.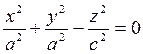

ЭЛЛИПСОИД

Определение 1. Эллипсоидом называется поверхность, которая в некоторой прямоугольно декартовой системе координат задается каноническим уравнением 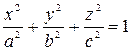, (1), где 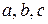- полуоси эллипсоида.

Если a ≠ b, a ≠ c, b ≠ c, то эллипсоид трехосный.

Исследуем уравнение (1) и определим форму эллипсоида.

1. Точка О (0;0;0) не принадлежит эллипсоиду, так как ее координаты не удовлетворяют уравнению (1).

2. Переменные x, y, z входят в уравнение в четной степени, следовательно, если точка М(x, y, z) принадлежит поверхности, то ей будет принадлежать 7 точек: М₁ (-x, y, z); М₂ (x, - y, z); М₃ (x, y, - z); М₄ (- x, - y, z);

М₅ (- x, y, - z); М₆ (x, - y, - z); М₇ (- x, - y, - z).

Таким образом, эллипсоид фигура симметричная относительно всех координатных осей, координатных плоскостей, начала координат.

3. Найдем точки пересечения эллипсоида с осями координат:

С осью ОХ: y = z = 0. Из уравнения (1) следует, х² = а² , отсюда х = ± а.

А₁(а; 0; 0), А₂(-а; 0; 0).

С осью ОУ: x = z = 0. Из уравнения (1) следует, у² = b² , отсюда y = ± b.

В₁(0; ,b; 0), В₂(0; -b; 0).

С осью ОZ: y = х = 0. Из уравнения (1) следует, z ² = с² , отсюда z = ± с.

С₁(0; 0; с), С₂(0; 0; -с).

Точки А₁(а; 0; 0), А₂(-а; 0; 0), В₁(0; ,b; 0), В₂(0; -b; 0). С₁(0; 0; с), С₂(0; 0; -с) – называются вершинами эллипсоида.