ЦИЛИНДРИЧЕСКИЕ ПОВЕРХНОСТИ
План: 1. Определение цилиндрических поверхностей.
2. Классификация цилиндрических поверхностей.
Вопрос
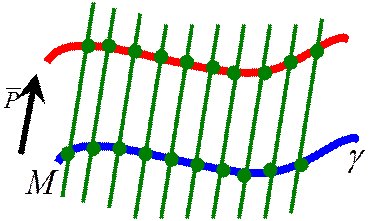 Определение 1. Поверхность, обладающая тем свойством, что вместе с каждой своей точкой М она содержит всю прямую, проходящую через точку М, параллельно данному ненулевому вектору
Определение 1. Поверхность, обладающая тем свойством, что вместе с каждой своей точкой М она содержит всю прямую, проходящую через точку М, параллельно данному ненулевому вектору 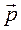 , называется цилиндрической поверхностьюили цилиндром.
, называется цилиндрической поверхностьюили цилиндром.
Цилиндрическая поверхность может быть образована следующим образом:
Пусть γ – некоторая линия, а 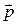 – ненулевой вектор. Поверхность, образованная всеми прямыми, каждая из которых проходит через некоторую точку линии γ ||
– ненулевой вектор. Поверхность, образованная всеми прямыми, каждая из которых проходит через некоторую точку линии γ || 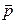 будет цилиндрической.
будет цилиндрической.
Эта линия γ называется направляющей поверхности, а параллельные прямые - образующими.
Теорема. Если направляющая цилиндрической поверхности в прямоугольной декартовой системе координат R=(O, 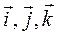 ) задана уравнениями
) задана уравнениями
γ: 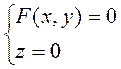 , а образующие ||
, а образующие || 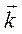 , то эта цилиндрическая поверхность определяется уравнением F(x, y)=0 (*).
, то эта цилиндрическая поверхность определяется уравнением F(x, y)=0 (*).
Рассмотрим только те цилиндрические поверхности, которые являются поверхностями второго порядка:
Определение 2.Поверхность, которая в некоторой декартовой системе координат задается уравнением 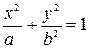 , называется эллиптическим цилиндром; поверхность, которая задается уравнением
, называется эллиптическим цилиндром; поверхность, которая задается уравнением 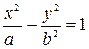 , называется гиперболическим цилиндром, а которая задается уравнением
, называется гиперболическим цилиндром, а которая задается уравнением 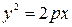 называется параболическим цилиндром.
называется параболическим цилиндром.
Для того чтобы построить поверхности, задаваемые этими уравнениями достаточно построить на плоскости 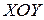 направляющую, уравнение которой на этой плоскости совпадает с уравнением самой поверхности, и затем через точки направляющей провести образующие параллельно оси
направляющую, уравнение которой на этой плоскости совпадает с уравнением самой поверхности, и затем через точки направляющей провести образующие параллельно оси 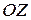 . Для наглядности следует построить также одно-два сечения плоскостями, параллельными плоскости
. Для наглядности следует построить также одно-два сечения плоскостями, параллельными плоскости  . В каждом таком сечении получим такую же кривую, как и исходная направляющая.
. В каждом таком сечении получим такую же кривую, как и исходная направляющая.
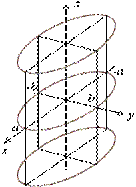

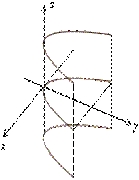
Примечание: Аналогично, если образующие цилиндрической поверхности параллельны другим осям координат, то такая цилиндрическая поверхность задается уравнениями:
1. В плоскости ХОZ:
Направляющая цилиндрической поверхности задана уравнениями
γ: 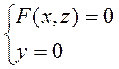 , а образующие ||
, а образующие || 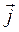 , то эта цилиндрическая поверхность определяется уравнением F(x, z)=0 (*).
, то эта цилиндрическая поверхность определяется уравнением F(x, z)=0 (*).
2. В плоскости YОZ:
Направляющая цилиндрической поверхности задана уравнениями
γ: 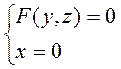 , а образующие ||
, а образующие || 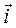 , то эта цилиндрическая поверхность определяется уравнением F(y, z)=0 (*).
, то эта цилиндрическая поверхность определяется уравнением F(y, z)=0 (*).
Вопрос
Пересечем цилиндрическую поверхность плоскостями, непараллельными ее образующим. В сечении получаются различные линии (эллипс, гипербола, парабола). Поэтому цилиндрическая поверхность называется эллиптической, гиперболической, параболической.
Классифицировать цилиндрические поверхности можно на основании вида направляющей. Существует 9 классов цилиндрических поверхностей.
Если прямоугольную декартову систему координат R=(O, 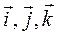 ) выбрать так, чтобы образующие цилиндрической поверхности были параллельны вектору
) выбрать так, чтобы образующие цилиндрической поверхности были параллельны вектору 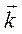 , а направляющая линия γ в системе координат R=(O,
, а направляющая линия γ в системе координат R=(O, 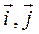 ) имела каноническое уравнение, то цилиндрическая поверхность определяется следующими уравнениями.
) имела каноническое уравнение, то цилиндрическая поверхность определяется следующими уравнениями.
| № | Каноническое уравнение | Название | Изображение |
| 1. | 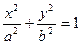
| Эллиптический цилиндр | 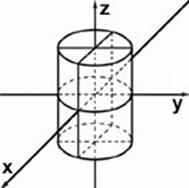
|
| 2. | 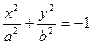
| Мнимый эллиптический цилиндр | Нет изображения |
| 3. | 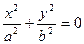
| Пара мнимых плоскостей пересекающихся по действительной прямой (ось OZ) | 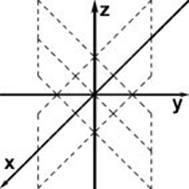
|
| 4. | 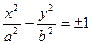
| Гиперболический цилиндр | 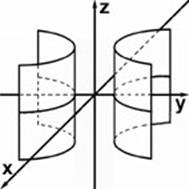
|
| 5. | 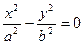
| Пара плоскостей пересекающихся по OZ | 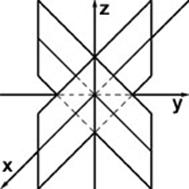
|
| 6. | 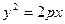
| Параболический цилиндр | 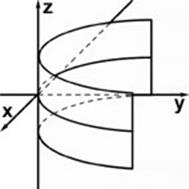
|
| 7. | 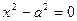
| Пара параллельных плоскостей | 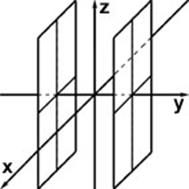
|
| 8. | 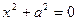
| Пара мнимых параллельных плоскостей | Нет изображения |
| 9. | 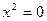
| Пара совпадающих плоскостей по YOZ | 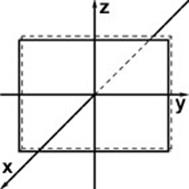
|

Дата добавления: 2018-09-24; просмотров: 3338;
